Predefinição:Manutenção/Categorizando por assunto
Esta página ou se(c)ção precisa ser formatada para o padrão wiki. (Agosto de 2019) |

Em física e demais ciências naturais, magnetismo é a denominação associada ao fenômeno ou conjunto de fenômenos relacionados à atração ou repulsão observada entre determinados objetos materiais - particularmente intensas aos sentidos nos materiais ditos ímãs ou nos materiais ditos ferromagnéticos - e ainda, em perspectiva moderna, entre tais materiais e condutores de correntes elétricas - especificamente entre tais materiais e portadores de carga elétrica em movimento - ou ainda a uma das parcelas da interação total (Força de Lorentz) que estabelecem entre si os portadores de carga elétrica quando em movimento - explicitamente a parcela que mostra-se nula na ausência de movimento de um dos dois, ou de ambos, no referencial adotado.[1][2] Há de se ressaltar que a simples observação de atração ou repulsão entre dois objetos não é suficiente para caracterizar a interação entre os dois como de origem magnética, geralmente confundindo-se com certa facilidade, aos olhos leigos, os fenômenos magnéticos e elétricos. Tais fenômenos elétricos e magnéticos, apesar de hoje saber-se estarem profundamente correlacionados, são comumente considerados e analisados como fenômenos distintos.
Aos olhos desatentos enfatiza-se que os fenômenos elétricos e magnéticos - ao menos no cotidiano - diferem entre si basicamente nos seguintes aspectos:[3]
- No cotidiano a força magnética mostra-se geralmente mais intensa do que a elétrica;
- Enquanto os fenômenos elétricos - em específico os eletrostáticos oriundos do atrito entre materiais diferentes - apresentem natureza efêmera, os magnéticos são geralmente duradouros;
- Ao passo que corpos eletrizados interagem de forma perceptível com praticamente todos os materiais, os corpos magnéticos interagem de forma significativa apenas com um grupo muito seleto desses;Predefinição:Nota de rodapé
- Em particular, é válido aqui desfazer-se a ideia em senso comum de que os ímãs atrairiam qualquer metal.Predefinição:Nota de rodapé Em verdade, a grande maioria dos metais simplesmente não responde em magnetostática de forma perceptível aos sentidos. Entre os poucos que respondem, destacam-se o ferro, o cobalto e o níquel.
- O magnetismo pode orientar os corpos em direções definidas, geralmente não ocorrendo o mesmo nos fenômenos elétricos. Em outras palavras, em virtude de sua orientação, um mesmo corpo magnético pode ou ser atraído ou ser repelido por outro. No caso elétrico ou os dois geralmente ou se atraem ou se repelem - de forma independente da orientação espacial destes;Predefinição:Nota de rodapé
- Os polos elétricos - positivo e negativo - podem ser separados ao passo que os polos magnéticos - norte e sul - estão sempre presentes no mesmo corpo, nunca podendo ser separados.Predefinição:Nota de rodapé
Nestes termos é fácil agora caracterizar a atração entre o pente de cabelos após uso e pequenos pedaços de papel, ou mesmo entre a folha de papel e a capa de plástico de uma encadernação, como fenômenos elétricos, e a atração entre uma chave de fenda e um parafuso, ou entre o adesivo de propaganda e a geladeira, como magnéticos.
O exemplo mais difundido de fenômeno magnético certamente associa-se o funcionamento da bússola, uma agulha magnética de livre movimento orientada pelo campo magnético terrestre.[4] As auroras boreal e austral constituem um exemplo menos conhecido, sendo devidas à existência de interação magnética entre partículas presentes no vento solar e o campo magnético da terra - que desvia tais partículas em direção aos polos magnéticos do planeta, onde, em interação com a atmosfera, implicam as luzes no céu características deste fenômeno.[1]
Magnetismo é ainda o nome associado à divisão da Física responsável pelo estudo dos fenômenos magnéticos. A descoberta e melhor compreensão da estreita relação existente entre os fenômenos magnéticos e elétricos implicou, em tempos recentes, na fusão das áreas concernentes ao estudo da eletricidade e magnetismo - originalmente distintas - em uma única divisão mais abrangente, o eletromagnetismo.[5] O eletromagnetismo encerra em si todos os fenômenos elétricos, todos os magnéticos, e mais os fenômenos associados à inter-relação explícita ou implícita entre os dois primeiros.
Predefinição:Sidebar with collapsible lists
Introdução
Um pouco de História

As observações de fenômenos magnéticos naturais são muito antigas. Entre elas relatam-se com frequência as realizadas pelos gregos em uma região da Ásia conhecida por Magnésia,[2] embora haja indícios de que os chineses já conheciam o fenômeno há muito mais tempo.[6] Ainda no século VI a.C., Tales de Mileto, em uma de suas viagens ao continente (na época província da Grécia), constatou que pequenas pedrinhas tinham a capacidade de atrair tanto objetos de ferro quanto a de atraírem-se. Tales foi o primeiro a tentar explicar o fenômeno afirmando que a magnetita - o minério magnético presente no solo - seria possuidor de uma espécie de "alma",[7] e que esse poderia comunicar "vida" ao ferro inerte, que por sua vez também adquiria o poder de atração.[6] Tales não teria sido contudo o primeiro a descobrir tal fenômeno na região. Conta a lenda que um pastor de ovelhas, de nome Magnes, teria percebido que a ponta de ferro do seu cajado ficava presa quando este o encostava em determinadas pedras[7] - presumidamente a magnetita. Segundo alguns autores, do nome da região derivou-se o termo "magnetismo", até hoje usado para estudar os fenômenos relacionados. Contudo para outros o termo "magnetismo" advém do nome do pastor de ovelhas que teria constatado o primeiro fenômeno "magnético".[8]
Em vista do que se sabe hoje em dia a explicação de Tales de Mileto pode parecer-nos muito simplória, contudo ressalva-se que não se deve julgar um pensamento fora do contexto histórico-sócio-cultural o qual pertence. Em tal época justamente os primeiros passos de uma longa jornada que viria culminar no que conhecemos hoje, dois milênios e meio depois, por ciência, estavam por ser dados. Em verdade, explicações similares perduraram pelos vários séculos que se seguiram: o magnetismo seria então a consequência da emanação de eflúvios, um "perfume" que emanaria do ferro e da magnetita, sensibilizando-os para que se atraíssem. A própria palavra ímã derivar-se-ia mais tarde da palavra francesa aimant, que, não de surpreender, traduz-se por amante em português.[6]
Os chineses foram certamente os primeiros a encontrar aplicações práticas para o magnetismo. No início da era cristã os adivinhos chineses já utilizavam um precursor da bússola, uma colher feita de magnetita que, colocada em equilíbrio sobre um ponto de apoio central, podia mover-se livremente. Tratava-se da "colher que apontava para o sul", sempre presente em seus rituais.[9] No século VI os chineses já dominavam a tecnologia para a fabricação de ímãs.[6]
Esses fenômenos, contudo, não despertaram um maior interesse, pelo menos até os século XIII, quando começaram a surgir observações e trabalhos mais acurados a respeito da eletricidade e do magnetismo. Delas decorreram de imediato a conclusão de que os fenômenos elétricos e magnéticos teriam naturezas completamente distintas, ideia que perdurou até dois séculos atrás. Em 1269 Pierre de Maricourt, em uma de suas cartas enviadas a um amigo, descreve com precisão a maioria das experiências típicas associadas ao fenômeno e que ainda hoje figuram com abundância em livros de ensino atuais.[10] A ele devemos as nomenclaturas "pólo norte" e "pólo sul" associadas aos pólos de um magneto e a lei dos "opostos se atraem, iguais se repelem" diretamente associada aos mesmos. Também observou que em um ímã, mesmo quando oriundo de fratura de outro, encontram-se presentes sempre dois pólos opostos.[6]
Destacam-se seguindo-se a cronologia e dando continuidade ao trabalho de Pierre de Maricourt, dois séculos mais tarde entretanto, os trabalhos do cientista inglês William Gilbert, esses resumidos em um livro publicado em 1600 que revelou-se um marco na área: o De Magnete.[11] Consonante com o fato de que a ciência em sua definição moderna vinha à luz no exato período em questão (William fora contemporâneo de Galileu Galilei) pode considerar-se esse livro como um dos primeiros trabalhos em moldes científicos sobre o assunto, e por tal um clássico da literatura científica. O tomo encerrava praticamente todos os conhecimentos válidos produzidos até a época, pouco acrescendo-se aos mesmos até o início do século XIX. Gilbert fora capaz inclusive de explicar o comportamento da bússola, propondo que a terra comportava-se como um ímã de dimensões gigantescas.[6] Conclusões mais sofisticadas, como a descoberta de que o aquecimento de um ímã fá-lo perder suas propriedades magnéticas e a verificação de que a magnetização e desmagnetização não implicam alteração no peso do objeto também estavam presentes. O livro não encerrava apenas estudos sobre magnetismo; também abordava vários dos tópicos contemporâneos ligados ao estudo da eletricidade.[12]
Os avanços seguintes na área do magnetismo só foram possíveis graças a um significativo avanço ocorrido na área da eletricidade: a invenção da pilha por Alexandro Volta.[13] A existência de uma fonte de energia elétrica - de corrente elétrica - duradoura mostrar-se-ia essencial para que o físico e químico dinamarquês Hans Christian Ørsted pudesse estabelecer de forma sólida em 1820, via um momento de serendipidade em uma aula e não nos confinamentos de um laboratório de pesquisa, algo do qual já se suspeitava há muito: que os fenômenos elétricos e magnéticos guardam íntima relação. A experiência de Ørsted entrou para os anais da física ao evidenciar que correntes elétricas provocam efeitos magnéticos em sua vizinhança, sendo estas capazes de interferir na orientação de bússolas em suas proximidades.[14]
O passo seguintes no avanço da compreensão do magnetismo em direção ao eletromagnetismo foi dado pelo inglês Michael Faraday e concomitantemente pelo estadunidense Joseph Henry: a descoberta da indução magnética.[15][16] Trata-se tão somente da resposta experimental afirmativa para uma questão diretamente decorrente da experiência de Ørsted: se eletricidade é capaz de produzir fenômeno magnético, é o inverso também verdade? Devido aos exaustivos estudos realizados por Faraday em detrimento de uma devoção menor por parte de Henry ao assunto - decorrente da sua indisponibilidade de tempo por razões profissionais - historicamente credita-se a Faraday e não a Henry os louros da descoberta.
A Faraday também credita-se o conceito de campo, conceito este imediatamente estendido tanto ao estudo da eletricidade quanto ao do magnetismo e que mostrar-se-ia essencial à síntese realizada por James Clerk Maxwell. Em tal contexto as contribuições de Heirinch Friedrich Emil Lenz (a lei de Lenz); de Wilhelm Eduard Weber, homenageado ao estabelecer-se a unidade S.I. para a grandeza fluxo magnético (o weber), sendo quem primeiro obteve a partir de experimentos relacionados ao eletromagnetismo o valor experimental de uma constante, c = 3,1 x 108 m/s, imediatamente reconhecida como análoga ao valor da velocidade da luz no vácuo; dos matemáticos Franz Ernst Neumann (lei de Faraday-Neumann-Lenz), Carl Friedrich Gauss (Lei de Gauss) e demais; não podem deixar de ser mencionadas.
Maxwell, com suas famosas quatro equações - as Equações de Maxwell - conseguiu explicar não apenas todo o conhecimento empírico sob o domínio do magnetismo quando sob domínio da eletricidade - e comuns - conhecidos até a sua época como também conseguiu estabelecer bases teóricas sólidas quanto à existência das ondas eletromagnéticas, o que ao fim da história abriu, junto os trabalhos de Weber, Hertz e outros, o caminho para a integração da ótica ao agora chamado eletromagnetismo.[8] E não demorou muito para evidenciar-se que a igualdade entre o valor teórico da velocidade das ondas eletromagnéticas oriundos das equações de Maxwell, o valor da constante experimentalmente determinado por Weber, o valor da velocidade das ondas eletromagnéticas determinado após a descoberta destas por Hertz, e o valor experimental da velocidade da luz - há algum tempo conhecido com razoável precisão - não se devia, certamente, a uma mera coincidência.[17]
Credita-se à Heinrich Hertz a confirmação experimental da existência das ondas eletromagnéticas e determinação da velocidade dessas.[18]
Polos e dipolos magnéticos
A principal característica de um objeto em interação magnética atrela-se ao fato de essa interação mostrar-se particularmente intensa em determinadas regiões e menos intensas em outras ao longo de sua extensão ou, em caso de tamanho desprezível, ao redor desse. A cada uma dessas regiões de forte interação dá-se o nome de polo magnético.[5] Evidencia-se que um polo é sempre acompanhado de um polo conjugado, havendo no mínimo dois polos distintos em qualquer objeto magnético. Tais polos são inseparáveis, e juntos formam o que denomina-se dipolo magnético.

Os polos conjugados de um objeto magnético são nomeados respectivamente polo magnético norte e polo magnético sul.
É explicitamente importante aqui que se evite confundir essa nomenclatura com a nomenclatura muito semelhante utilizada para nomearem-se os polos geográficos de objetos em rotação; em particular os polos geográficos do planeta Terra. Associados a um objeto em rotação têm-se os polos geográficos. Fala-se neste caso em polo geográfico norte e polo geográfico sul: considerando-se os dois pontos determinados pelo interseção do eixo de rotação com a superfície do objeto girante, movendo-se os dedos da mão direita sobre o mesmo de forma que os dedos dessa mão, em posição de segurá-lo, acompanhem o seu movimento de rotação, ter-se-á o dedão dessa mão indicando o polo que será então denominado polo geográfico norte; outro dos dois pontos na superfície será o polo geográfico sul.
A definição de qual dos polos magnéticos de um eletroímã será nomeado polo magnético norte e qual será o polo magnético sul também pode, em vista do paradigma científico válido atualmente, ser determinada mediante uma das aplicações da "regra da mão direita"; obviamente não existindo neste caso um eixo de rotação espacial aplicável, contudo. A referência é nesse caso a direção e sentido estabelecidos pela corrente elétrica diretamente associada ao comportamento magnético observado, corrente essa que geralmente percorre o condutor elétrico, espira ou solenoide em consideração. Estabelecido qual é o polo norte e qual o polo sul magnéticos desse, por comparação, estabelece-se qual o polo norte e qual o sul de qualquer outro magneto. Para tal basta observar que, dados dois objetos em interação magnética:
- polos de mesma nomenclatura, quando em interação, determinam repulsão;
- polos de nomenclaturas diferentes, quando em interação, determinam atração.
É sabido, entretanto, que a nomenclatura magnética em debate antecede cronologicamente o conhecimento necessário ao uso da regra da mão direita para determiná-la. A explicação para a questão derivada passa certamente pela percepção de que a semelhança entre as nomenclaturas para os polos geográficos e para os polos magnéticos talvez não seja, e em verdade não é, mera coincidência. Há muito, conforme citado, sabe-se que dipolos magnéticos, quando suspensos de forma que possam girar livremente, orientam-se espacialmente de forma que um de seus polos magnéticos determine uma direção próxima àquela estabelecida pelos polos geográficos da terra. Tal observação levou à denominação no magneto de polo magnético norte ao polo magnético que orienta-se de forma a indicar o polo geográfico norte, e à de polo magnético sul ao polo magnético do magneto voltado para o sul geográfico da Terra. Essas nomenclaturas conforme estabelecidas são - ao menos na atualidade visto que os polos magnéticos do planeta alternaram suas posições geográficas com o passar das eras - condizentes com as estabelecidas pelos usos antes citados da regra da mão direita.
A Terra é um grande ímã


Durante muito tempo procurou-se explicação para a orientação assumida pelos ímãs quando suspensos de forma a girarem livremente. A resposta é em princípio simples quando se propõe que a Terra se comporta como um ímã de dimensões gigantescas, contudo mostra-se bem mais complicada quando evolui para a questão de se saber o porquê da Terra se comportar como um ímã.[19]
Em dias atuais os polos geográficos localizam-se próximos, mas não coincidentes, aos polos magnéticos da Terra. Em vista das considerações na seção anterior, é fácil perceber que próximo ao polo geográfico norte da Terra situar-se-á o polo sul magnético do planeta, e próximo ao polo geográfico sul do planeta encontra-se o polo magnético norte deste. Tal posicionamento leva ao correto funcionamento da bússola: o norte magnético da agulha magnética determina o norte geográfico do planeta por ter sido atraído pelo polo magnético sul do planeta, esse setentrionalmente localizado.
Em termos dos polos geográficos e do eixo de rotação do planeta, fundamentais para se definirem as coordenadas geográficas, as posições geográfica dos polos magnéticos são atualmente as seguinte:[20]
| Pólo magnético norte[1] | |||
| Pólo magnético sul[2] |
Vale contudo lembrar que a bússola nem sempre irá apontar exatamente para tais pontos. Devido a interferências associadas às condições magnéticas locais, devidas entre outros à presença ou não de materiais magnéticos no solo, mesmo o uso da bússola para a orientação geográfica deve ser feito com cautela, devendo esta ser atrelada a uma correção pontual conhecida por declinação magnética. As cartas de navegação normalmente informam a declinação magnética aplicável e sua área de abrangência.
A explicação do porquê a Terra se comporta como um grande ímã mostra-se bem mais nebulosa ao considerar-se que os registros magnéticos gravados em rochas vulcânicas - nos ímãs naturais, verdadeiros "fósseis" magnéticos - fortemente sugerem que as posições geográficas dos polos magnéticos do planeta mudam não apenas constantemente - conforme corroborado por medidas atuais - como em verdade mudam radicalmente. Nos últimos 17 milhões de anos, tempo não tão significativo perto dos 4,5 bilhões de anos atribuídos à idade do planeta, os polos magnéticos teriam invertido suas posições cerca de 170 vezes.[6] Mesmo considerações sobre o fato de que o manto e o núcleo da Terra sejam constituídos em essência por ferro não são suficientes para estabelecer-se um modelo satisfatório. Sabe-se que o material do manto encontra-se em estado líquido viscoso, em temperaturas bem acima da temperatura de Curie deste elemento, o que o leva a um estado não magnético. A mesma consideração, quando aplicada ao núcleo, mesmo este sendo sólido, mostra-se também pertinente. Até o momento não se tem um modelo cientificamente aceito para explicar o magnetismo terrestre e seu comportamento. Supõe-se que correntes elétricas oriundas de gradientes de temperatura no interior do planeta desempenhem papel importante no processo.
No âmago do fenômeno
Conforme citado, não se verificou, até os dias de hoje, a existência de cargas magnéticas - de monopolos magnéticos - na natureza. Eis pois que surge a questão: qual a causa primária responsável pelos fenômenos magnéticos observados na natureza? A resposta é simples: cargas elétricas em movimento, ou seja, correntes elétricas.
Quando duas partículas eletricamente carregadas encontram-se estáticas no referencial adotado, há entre elas uma interação de natureza puramente elétrica. Caso apenas uma delas esteja em movimento retilíneo uniforme, ainda haverá entre elas apenas uma interação de natureza elétrica. Contudo, colocando-se ambas em movimento retilíneo uniforme, observar-se-á no referencial adotado que, além da interação elétrica entre as mesmas, uma nova forma de interação - a interação magnética - far-se-á presente. As cargas foram colocadas em movimento retilíneo uniforme por simplicidade, havendo entre as mesmas interação magnética mesmo no caso em que estas encontrem-se aceleradas, desde que ambas, contudo, apresentem velocidades não nulas. A escolha de sistemas envolvendo apenas cargas em movimento retilíneo uniforme é geralmente assumida quando estuda-se o magnetismo em virtude de que, em sistemas envolvendo cargas elétricas aceleradas, haverá ainda um terceiro fenômeno envolvido: a emissão de ondas eletromagnéticas. Tal fenômeno resume-se geralmente na seguinte sentença: "cargas elétricas aceleradas irradiam".[21] A necessidade de se considerar as interações oriundas da radiação presente em tais sistemas certamente torna-os mais complexos, sendo estes estudos no contexto do eletromagnetismo.[22]
O estudo dos fenômenos associadas à interação magnética em sistemas envolvendo apenas cargas elétricas em movimento retilíneo uniforme - ou em sistemas onde a quantidade total de onda eletromagnética irradiada pode ser desprezada - é geralmente designado por magnetostática.
Em essência, todo magnetismo conhecido atrela-se de alguma forma à presença de cargas elétricas em movimento. Mesmo em ímãs naturais, materiais onde não se verifica a presença de correntes macroscopicamente mensuráveis em suas estruturas, tal afirmação é valida. O magnetismo em ímãs naturais e demais materiais magnéticos associa-se à cinemática das cargas elétricas - prótons e elétrons, com destaque para os últimos - presentes em suas estruturas microscópicas, ou seja, nos átomos que os compõem. Em vista dos modelo atômicos de Rutherford-Bohr para o átomo, os elétrons movem-se em órbitas em torno do núcleo - produzindo por tal cada qual um efeito magnético. Mesmo em vista do modelo mais moderno para o átomo - o modelo atômico dos orbitais - derivado de avanços na compreensão da mecânica quântica, tal afirmação ainda é plenamente válida.
As propriedades magnéticas de um material são decorrentes da forma como os diversos dipolos magnéticos oriundos das correntes elétricas em suas estruturas atômicas se combinam entre si, tanto em nível interno ao próprio átomo - o que se refere sobretudo à interação magnética entre si dos elétrons que o estruturam - como entre um átomo e seus demais vizinhos. Há de se considerar também em qualquer dos modelos citados que o magnetismo associado a uma partícula carregada em particular, seja esta próton ou elétron, não se deve apenas ao seu movimento relativo no referencial adotado. Há também, de grande relevância à análise do comportamento magnético - e da própria estruturação do átomo como descrito - o momento magnético intrínseco de cada partícula, este diretamente correlacionado ao spin - ao momento angular intrínseco - da referida partícula. É sabido que associar o momento angular intrínseco de uma partícula ao movimento de rotação desta sobre seu eixo não é um dos melhores modelos para se explicar tal propriedade - mesmo porque partículas como o elétron não têm dimensão experimentalmente resolvida (o elétron é até o momento descrito como um ponto) - contudo este modelo serviria de base para justificar a correlação entre os momentos angular e magnético intrínsecos das partículas carregadas: uma partícula carregada que gira sobre si implica carga elétrica em movimento circular e, por tal, em campo magnético. Partículas carregadas como elétrons e prótons são, por si só, pequenos dipolos magnéticos e os efeitos magnéticos destes são fundamentais tanto para a compreensão da estrutura do átomo como do comportamento magnético da matéria como um todo.[23]
Os momentos de dipolo magnéticos
Dipolo extrínseco
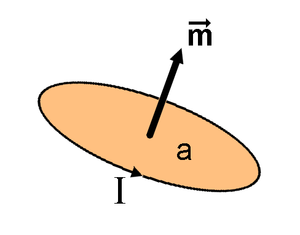
Considere uma pequena superfície plana circular de área "a" delimitada pela presença de uma corrente elétrica de intensidade constante "i" junto ao perímetro desta. Define-se o momento de dipolo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } associado a esta pequena espira de corrente elétrica como:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m = i \vec a }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec a } representa o "vetor área", um vetor cujo valor corresponde ao valor da área encerrada pela fronteira, cuja direção é perpendicular à superfície plana em questão e cujo sentido é adequadamente estabelecido pela regra da mão direita.
Embora tenha-se assumido um anel circular de corrente para estabelecer-se a definição de momento de dipolo magnético, é importante ressaltar que, provido que a corrente esteja confinada a um plano, a expressão constitutiva anterior permanece válida qualquer que seja a forma do circuito de corrente a se considerar, sendo o módulo do momento de dipolo determinado, em ambos os casos, pelo produto entre os valores da área "a" da superfície confinada e da corrente "i" presente em seu perímetro.[24]
Assim como a carga elétrica - no Sistema Internacional de Unidades (S.I.) medida em coulombs - representa a fonte primária responsável pelos efeitos elétricos, o momento de dipolo magnético corresponde à fonte primária responsável pelos efeitos magnéticos, sendo seu papel na magnetostática em muito similar ao da carga elétrica na eletrostática. Contudo, ao passo que a carga elétrica é uma grandeza escalar, o momento de dipolo magnético é certamente uma grandeza vetorial, e estas não são completamente análogas.
A unidade de medida do momento de dipolo magnético é o ampère metro quadrado (A.m²), correspondendo, conforme esperado, ao produto das unidades adotadas no S.I. para a corrente elétrica e para a medida de área, respectivamente.
Para superfícies não planas ou com bordas irregulares, pode-se determinar o momento de dipolo magnético associado mediante auxílio do cálculo integral e diferencial:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m = I \int {d \vec a} }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \vec a } representa o vetor área associado a cada um dos infinitesimais de área no qual a superfície é dividida.[22]
Dipolo intrínseco
Partículas subatômicas carregadas - a exemplo elétrons e prótons - portam-se cada qual como pequenos magnetos, possuindo um momento de dipolo magnético inerente à partícula, denominado momento de dipolo magnético intrínseco. Este momento de dipolo magnético relaciona-se diretamente a outra propriedade pertinente a todas as partículas subatômicas, carregadas ou não: o momento angular intrínseco, também denominado spin. Conforme já discutido, ambas as propriedades não têm análogos clássicos, e o modelo de se pensar em uma partícula girando sobre seu próprio eixo não se mostra plenamente satisfatório, embora traga alguma luz à relação existente entre tais propriedades. Momento angular é uma grandeza notoriamente associada à dinâmica de rotação, e se a partícula possui carga, ter-se-á também, por lógica, um momento de dipolo magnético, visto encontrar-se esse notoriamente associado à pertinente dinâmica da atrelada carga elétrica.
Ressalva feita às diminutas dimensões (ver Campo magnético de um dipolo) e excetuando-se a natureza não clássica desses, os momentos de dipolo magnéticos intrínsecos das partículas carregadas portam-se para todos os efeitos de forma análoga aos momentos magnéticos extrínsecos antes definidos.
Os momentos magnéticos intrínsecos para o elétron e para o próton são, respectivamente:[1]
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_e = 9,28 \times 10^{-24} A.m^2 }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_p = 1,41 \times 10^{-26} A.m^2 }
Alguns momentos magnéticos
A tabela abaixo apresenta alguns momentos de dipolo magnéticos para comparação.[1] Os valores aparecem em notação científica.
| Núcleo do átomo de nitrogênio | |
| Próton | |
| Elétron | |
| Átomo de nitrogênio | |
| Bobina de um galvanômetro típico | |
| Pequena barra imantada | |
| Bobina supercondutora | |
| A Terra |
Campo magnético
Um pouco sobre campos
Antes do conceito de campo ser estabelecido dentro da física admitia-se que as interações físicas, quaisquer que fossem suas naturezas, davam-se por ação direta e instantânea de uma das partes interagentes sobre a outra e vice-versa, em um modelo conhecido por "ação à distância". Neste modelo, em essência, não havia um ente físico responsável por intermediar a interação.
Surgindo entre outros como um mecanismo para facilitar os cálculos envolvidos em problemas onde havia inúmeros - ou às vezes incontáveis - objetos que, dispostos simetricamente, atuavam simultaneamente sobre o ente físico em análise, o conceito de campo evoluiu rapidamente junto às descobertas de novos fatos que contrastavam com a ideia de ação à distância, chegando-se ao ponto deste ganhar, nos paradigmas válidos atualmente, status de ente físico com existência real. A possibilidade de verificar-se experimentalmente que "o limite superior para a velocidade de transmissão de uma informação é a velocidade da luz" foi certamente decisivo a favor da ideia de campo: o campo hoje expressa uma entidade real responsável por mediar a interação entre dois entes físicos quaisquer. Há pois um campo associado à interação gravitacional, um associado à interação elétrica, um associado à interação magnética, e assim por diante. As ondas eletromagnéticas figuram como o ápice de tal ideia: um campo elétrico e um campo magnético sustentando-se mutuamente de forma a propagarem-se livremente pelo espaço.
Têm-se pois os seguintes modelos físicos:
- (1): ente 1 <-- ação à distância: direta e instantânea --> ente 2 : superado; contradito por fatos descobertos nos últimos séculos.
- (2): ente 1 <-- Campo: ação não direta e não instantânea --> ente 2: paradigma atual

Nos termos do modelo atual a interação magnética entre dois momentos de dipolo magnéticos é analisada sob enfoque de um campo, neste caso uma entidade vetorial conhecida por campo magnético. Sua definição tem origem em fatos empíricos, sendo o mesmo definido como se segue.
Definição
Considere uma carga elétrica de prova positiva q = e+ movendo-se com uma velocidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } não nula em uma região do espaço sob influência apenas de fontes magnéticas - a exemplo, sob influência de fios que conduzem correntes elétricas, ou mesmo de uma distribuição não necessariamente simples de dipolos magnéticos. Nestes termos verifica-se experimentalmente que:
- havendo presença de força magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M } atuando na partícula, esta será sempre perpendicular à velocidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } desta partícula.
- mantidas demais condições inalteradas, o valor da força magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M } é diretamente proporcional ao valor da carga q da partícula.
- mantidas demais condições inalteradas, o valor da força magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M } é diretamente proporcional ao valor v da velocidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } da partícula.
- variando-se apenas a direção da velocidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } da partícula, para cada ponto há uma direção em específico para a qual o valor da força magnética mostrar-se-á nulo.
- o valor da força magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M } depende do ângulo existente entre a direção da velocidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } da partícula e a direção anterior - para a qual a força magnética mostra-se nula. O fator de proporcionalidade envolve o seno do ângulo em questão (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle sen \theta } ).
Agrupando-se logicamente estes dados chega-se à conclusão de que a força magnética que atua sobre uma carga elétrica q em movimento é proporcional ao produto das grandezas relacionadas:
- F Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha } Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q.v.sen \theta }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha } é traduzido por "é diretamente proporcional a". O rigor matemático permite-nos transformar tal sentença em uma igualdade mediante a introdução de uma constante, aqui nomeada B.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F= B(q.v.sen \theta) }
A contante B corresponderá, por definição, justamente ao valor do campo magnético presente no ponto em que a partícula se encontra, ficando este por tal assim definido:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B = \frac {F_M}{q.v.sen \theta} }
O valor do campo magnético B fica experimentalmente definido visto que as demais grandezas das quais depende - velocidade, força e ângulo - são facilmente mensuráveis na prática. Contudo há ainda que se considerar a direção e sentido do campo magnético B, pois este é em verdade uma grandeza vetorial. Assim:
- a direção do campo magnético B é definida como sendo paralela à direção da velocidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } da partícula carregada para no caso em que a força magnética sobre a mesma mostre-se nula em virtude apenas da orientação desta velocidade.
- o sentido do campo magnético é estabelecido de forma a ter-se o sentido do campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } análogo ao sentido do vetor que resulta do produto vetorial entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } na ordem dada, ou seja, análogo ao sentido do resultado do produto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M \times \vec v } .
Em essência, esta definição implica a regra da mão direita conforme amplamente difundida, de forma que:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M = q. \vec v \times \vec B }
Esta é a expressão fundamental da interação magnética, que permite calcular a força magnética que atua em uma partícula que se mova com uma velocidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } em uma região do espaço onde haja um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } . Esta equação encerra em si todos os pontos empíricos inicialmente discutidos, inclusive o fato experimental de que a força magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M } mostra-se sempre perpendicular à velocidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } da partícula, e também sempre perpendicular ao agora definido campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } , com o qual a partícula interage. O ângulo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } relativo ao ângulo entre os vetores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } , o qual pode certamente ser diferente de 90º, antes presente de forma explícita na equação envolvendo apenas os módulos das grandezas em questão, ainda figura na presente equação, contudo agora subentendido na definição de produto vetorial. O produto vetorial entre dois vetores paralelos é por definição nulo, de forma que se a partícula for posta a mover-se de forma paralela ao campo magnético, a expressão irá fornecer um resultado nulo para a força magnética, o que está em pleno acordo com os resultados experimentais: há uma direção em particular na qual a partícula se move de forma que esta não experimente força magnética - a direção definida como sendo a direção de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } .
A unidade de campo magnético deve ser dimensionalmente compatível com sua definição. Retomando a expressão que define o valor de B, lembrando que seno de um ângulo é adimensional e que, no S.I, a unidade para força é o newton (N), para velocidade é o metro por segundo (m/s), para carga elétrica é o coulomb (C), e que há uma relação entre as unidade de corrente elétrica, carga e tempo de forma que um ampère iguala-se a um coulomb por segundo (1A = 1C/s), tem-se que a unidade de campo magnético deve ser expressa por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [ \vec B ]= \frac {N}{C (\frac{m}{s})} = \frac{Ns}{Cm} = \frac {N}{A.m}}
onde os colchetes "[]" representam "a unidade de".
A unidade de campo magnético recebe o nome de tesla em homenagem ao cientista Nikola Tesla, de forma que
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [ \vec B ]= tesla = \frac {newton}{ampere.metro} } ou seja, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1T = \frac {N}{A.m}}
Segue-se abaixo uma tabela com alguns valores de campos magnéticos típicos:[22]
| Superfície de uma estrela de nêutrons | |
| Nas proximidades de um ímã supercondutor | |
| Nas proximidades de um grande eletroímã | |
| Nas proximidades de uma pequena barra imantada | |
| Campo magnético terrestre em sua superfície | |
| No espaço interestelar | |
| Em uma sala blindada magneticamente |
Há ainda uma unidade para o campo magnético que, embora não pertencente ao S.I, mostra-se frequentemente utilizada em laboratórios de física. Trata-se do Gauss, unidade nomeada em homenagem explicita a Johann Carl Friedrich Gauss, um matemático cujas contribuições foram decisivas na solidificação da teoria do eletromagnetismo (vide Lei de Gauss, entre outras). Um campo magnético de valor 1 gauss equivale a um campo de 1x10 -4 teslas, ou respectivamente, 1 tesla equivale a 10.000 gauss. O campo magnético da terra, quando medido em sua superfície, tem ordem de grandeza de 1 gauss.
Representações
O campo magnético é um campo vetorial. Traduz-se por tal que deve-se, a cada ponto do espaço tridimensional, associar um pequeno vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } com módulo, direção e sentido bem determinados, isto a cada instante especificado de tempo t, visto que o campo magnético pode encontrar-se variando no tempo (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \vec {B_{(\vec r ,t)}}} ). Há certamente diversas formas de representá-lo, tanto gráfica como algebricamente.
Representação algébrica
Observação: requer-se doravante conhecimentos básicos acerca de sistema de coordenadas bem como de espaço e álgebra vetoriais para a compreensão do que se apresenta.
Representar algebricamente tais campos é certamente a forma mais coerente de fazê-lo, bastando para tal associar uma função escalar das coordenadas espaciais (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r } ) do ponto onde determina-se o campo bem como do tempo t a cada um dos vetores unitários que definem o espaço tridimensional no sistema de coordenadas adotado, isso de forma a poder-se calcular o vetor campo magnético naquele ou em qualquer outro ponto ou tempo em questão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{\vec r, t} = f_{1(\vec r, t)} \vec {\hat u}_1 + f_{2(\vec r, t)} \vec {\hat u}_2 + f_{3(\vec r, t)} \vec {\hat u}_3 }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {{ \hat u }_1} , \vec {{ \hat u }_2} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {{ \hat u }_3} } representam os vetores unitários no sistema de coordenadas escolhido.
A exemplo, para um fio retilíneo infinito conduzindo uma corrente I ao longo do eixo coordenado Z em orientação dada por este, sabe-se que o campo magnético é circular em torno do fio, e que torna-se mais fraco à distâncias maiores desse (ver seção "O campo magnético e o fio retilíneo"). Em um sistema de coordenadas cartesiano pode-se expressá-lo por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \frac {\mu_0 I}{2 \pi [ \sqrt {x^2+y^2}]} ( [ - \frac {y}{ \sqrt {x^2+y^2}}] \vec {\hat i} + [\frac {x}{\sqrt {x^2+y^2}}] \vec {\hat j} ) }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat i} } representa o vetor unitário que define a direção e orientação do eixo coordenado X e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat j} } o unitário que define os mesmos parâmetros para o eixo coordenado Y. As coordenadas do ponto P = (x,y,z) onde determina-se o campo são representadas por x e y na referida equação, sendo notória contudo a ausência da coordenada z. Dada a simetria, o vetor campo magnético não dependente da coordenada z no caso de um fio retilíneo infinito, o que justifica a ausência dessa coordenada na equação que determina Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } .
Com a direção e sentido do eixo Z sendo definidos pelo vetor unitário Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat {k}} } o ponto P = (x,y,z) onde determina-se o campo é realmente localizado, a partir da origem O do sistema de coordenadas, pelo vetor posição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r = x \vec {\hat i} + y \vec {\hat j} + z \vec {\hat k} } . Dada a simetria axial do problema, contudo, é possível reduzi-lo a um problema bidimensional confinado ao plano ZY (onde z=0); assume-se assim doravante, sem perda de generalidade, que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r = x \vec {\hat i} + y \vec {\hat j} } , contudo.
A equação para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } trata-se apenas da expressão que define um vetor unitário tangente a uma circunferência de raio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = \sqrt {x^2 + y^2} } inscrita em plano paralelo ao plano XY, ou melhor, no plano XY mediante convenção bidimensional adotada, e com centro sobre o eixo z, ou seja, sobre a origem diante da convenção (o fator entre parênteses na expressão acima), expressão essa multiplicado pelo módulo do campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } associado a este raio em específico.
O módulo do campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B = \frac {\mu_0 I}{2 \pi [\sqrt {(x^2+y^2)}]} } decai com aumento da distância ao fio, ou seja, com o raio da circunferência, conforme visto.
O termo entre parênteses que se segue ao módulo do campo representa um vetor unitário Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat u}_{tangente} } tangente à circunferência. Isto é melhor visualizado lembrando-se que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [ \frac {y}{ \sqrt {x^2+y^2}}] = \frac {y}{r} } representa o seno do ângulo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } entre o vetor que localiza o ponto em questão a partir do fio e o eixo X, e que a expressão seguinte que acompanha o vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat j} } representa o cosseno do mesmo ângulo.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat u}_{tang.circ.} = - sen (\theta). \vec {\hat i} + cos (\theta). \vec {\hat j} }
O sinal de menos que acompanha o fator multiplicando o unitário Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat i} } garante a validade da regra da mão direita à situação.
Viu-se que o campo não tem componente paralela ao fio, ou seja, na direção unitária Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat k} } , e por tal o vetor campo magnético está sempre confinado a planos paralelos ao plano XY. Tal observação permite escrever o mesmo campo também em coordenadas polares, onde o mesmo se escreve:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \frac {\mu_0 I}{2 \pi r} \vec {\hat \theta} }
Neste sistema de coordenadas bidimensional os vetores unitários são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat r} } em direção radial e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat \theta} } em direção perpendicular ao primeiro. Vê-se que a escolha de um sistema de coordenadas que explore a simetria do campo em questão pode simplificar em muito sua expressão matemática. A expressão inicial para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } relativa ao sistema de coordenadas cartesiano é visivelmente igual à anterior uma vez visto que entre os sistemas cartesiano e polar há as seguintes relações:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat \theta} = [ - \frac {y}{ \sqrt {x^2+y^2}}] \vec {\hat i} + [\frac {x}{\sqrt {x^2+y^2}}] \vec {\hat j} = - sen (\theta). \vec {\hat i} + cos (\theta). \vec {\hat j} }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat r} = [ \frac {x}{ \sqrt {x^2+y^2}}] \vec {\hat i} + [\frac {y}{ \sqrt {x^2+y^2}}] \vec {\hat j} = cos (\theta). \vec {\hat i} + sen (\theta). \vec {\hat j}}
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r = r. \vec {\hat r} = x \vec {\hat i} + y \vec {\hat j} }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = | \vec r | = \sqrt {x^2+y^2} }
Representação gráfica

A representação gráfica rigorosa do campo magnético deveria compor-se pela representação de uma quantidade infinita de vetores - uma para cada ponto do espaço - no diagrama que representa o espaço em questão. Como isto é praticamente impossível, é de praxe representar-se apenas um número significativo de vetores - usualmente o menor número possível de forma a garantir-se a compreensão do comportamento do campo em questão no espaço considerado sem contudo comprometer a legibilidade do diagrama. Neste diagrama, cada vetor é desenhado no respectivo ponto a qual associa-se de forma que seu módulo seja proporcional ao seu comprimento no diagrama.
A figura ao lado fornece um exemplo da representação de um campo vetorial. Embora não específica ao magnetismo, seu campo é próximo do que se espera encontrar em um quadrupolo magnético com os polos localizados nos vértices da moldura.
Linhas de campo magnético
Olhando-se para os diagramas vetoriais que representam os campos de grandezas físicas vetoriais como o campo elétrico e o campo magnético facilmente percebe-se que os diversos vetores representativos destes campos, quando adequadamente desenhados, sugerem que os mesmos ordenam-se seguindo um padrão de linhas no diagrama. Em verdade percebeu-se que este padrão de linhas poderia constituir uma representação gráfica bem mais simples dos mesmos campos vetoriais considerados. É desejado que nesta representação por linhas não se perca nenhuma informação antes contida na representação original, contudo. Para que isto tornar-se possível, alguns critérios foram estabelecidos para representar-se um campo vetorial através das chamadas linhas de campo:
- o vetor campo em um dado ponto do espaço deve ser sempre tangente à linha de campo que passe por este ponto;
- as linhas devem ser orientadas em acordo com a orientação do vetor tangente em qualquer pondo em consideração;
- o módulo do vetor em um ponto deve ser proporcional à densidade volumétrica de linhas de campo na região em torno deste ponto.
Com tais observações é possível construir uma representação para o campo vetorial baseada apenas em linhas e não em representações dos vetores em si. Contudo a ideia central não pode ser esquecida: a grandeza fisicamente significativa é o vetor em cada ponto do espaço e não as linhas de campo em si, devendo o vetor ser inferido a partir da representação por linhas sempre que se fizerem necessárias aplicações do campo para soluções de problemas.
A representação mais comum de campos vetoriais é certamente a representação por linhas. As linhas representativas de um campo magnético são conhecidas como linhas magnéticas, ou linhas de campo magnético. Um nome inadequado é ainda utilizado, contudo sua utilização deve ser fortemente desencorajada: trata-se das famosas "linhas de força". O campo magnético não é um "campo de forças", embora este possa ser inferido a partir de um campo de "forças magnéticas máximas" que atuam sobre uma carga elétrica em movimento ao passar por cada ponto da região em questão. Repare que as linhas representativas do "campo de força magnética máxima" seriam perpendiculares às linhas que representam o campo magnético em si visto que a força magnética é sempre perpendicular ao vetor campo magnético no ponto em consideração (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {F_M} = q \vec v \times \vec B } ).
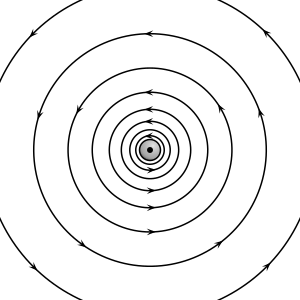
Abaixo tem-se a representação do campo magnético produzido por um dipolo magnético mediante a representação por linhas bem como sua representação algébrica. Repare que o campo é mais intenso perto do dipolo e mais fraco à distâncias maiores: as linhas se afastam umas das outras a medida que a distância ao dipolo aumenta. O campo é particularmente intenso nos lados direitos e esquerdo do dipolo, ou seja, nos polos magnéticos, e menos intensos em regiões externas a este ao longo de uma linha vertical que passe pelo seu centro. As linhas são orientadas, conforme pode-se observar, segundo a orientação dos vetores campo magnético existentes em cada ponto do espaço devidos ao dipolo.
O dipolo e o campo magnéticos
O dipolo magnético, quer intrínsecos quer extrínsecos, está no cerne da compreensão dos fenômenos magnéticos. Compreender sua relação com o campo magnético é fundamental à teoria associada.
Campo magnético de um dipolo
Dipolos magnéticos são certamente fontes de campos magnéticos e também sofrem o efeito desses quando em regiões onde os mesmo encontrem-se presentes.
Dado um dipolo magnético com dimensões desprezíveis situados na origem, o campo magnético por ele produzido em qualquer ponto ao seu redor pode ser determinado através da expressão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{(\vec r)} =\frac {\mu}{4 \pi} \frac {1}{r^3} [3 ( \vec m . \vec {\hat{r}})\vec {\hat{r}} - \vec m] } [22]
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu } representa uma constante que caracteriza magneticamente o meio no qual o momento de dipolo magnético encontra-se imerso - a permeabilidade magnética do meio, para o vácuo igual a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = \mu_0 = 4 \pi \times 10^{-7} N/{A^2} } (newtons por ampère quadrado, o mesmo que henry por metro [H/m]) - ; Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } representa o momento de dipolo magnético conforme definido em seção anterior; Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r } representa o vetor que localiza o ponto onde calcula-se o campo em relação ao dipolo magnético, dipolo suposto aqui situado na origem do sistema de coordenadas; Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat{r}} } representa o vetor unitário Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec u_r = \vec r/r } (módulo igual a 1, adimensional) direcionado do ponto onde se encontra o dipolo magnético até o ponto onde quer-se determinar o campo (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat{r}} = \vec u_r = \vec r / r } ); r representa o módulo do vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r } , ou seja, a distância em linha reta entre o dipolo e o ponto em questão, e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{(\vec r)} } representa o campo magnético no ponto definido por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r } . O "." refere-se aqui ao produto escalar de dois vetores.
Conforme escrita esta equação não encontra-se atrelada a um dado sistema de coordenadas em específico. É contudo usual orientar-se o momento de dipolo no sentido do eixo z tanto em um sistema de coordenadas polar como cartesiano.
O campo magnético produzido por um dipolo magnético extrínseco assemelha-se em muito - quando a grandes distâncias destes - ao campo magnético produzido por um dipolo intrínseco. A figura ao lado mostra esta comparação, expressando o campo magnético em torno desses através da usual representação por linhas de campo. No início tem-se a representação de um campo produzido por uma espira de corrente macroscópica, com a corrente "entrando" na folha de papel - ou tela - no lado inferior (círculo com um "X") e saindo dessa no lado superior (círculo com um ponto central). Reduzindo-se gradualmente as dimensões dessa espira, contudo mantendo-se o mesmo valor de momento de dipolo total, tem-se ao fim o campo de um dipolo magnético puntual ou intrínseco - então representado por uma pequena seta, ao centro.
Movendo-se em direção radial para longe do dipolo, para distâncias não muito próximas a esse o campo magnético que esse produz decai não com o quadrado mas sim com o cubo da distância ao mesmo. A título de informação, o campo elétrico oriundo de um dipolo elétrico comporta-se de maneira idêntica, sendo descrito por equação estruturalmente análoga.
Dipolo em um campo magnético

Colocando-se um momento de dipolo magnético puntual em um ponto do espaço onde haja um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } de origem externa, este dipolo magnético ficará sujeito a um torque que tende a fazê-lo girar e orientar-se em acordo com a direção do campo magnético externo. A bússola, imersa no campo magnético da terra, representa uma excelente aproximação da situação. O torque que faz o eixo de um motor elétrico girar corresponde justamente ao torque aplicado sobre o momento de dipolo magnético associado às espiras condutoras presas ao eixo (o rotor) quando imersas no campo magnético oriundo de ímãs permanentes ou eletroímãs fixos à carcaça do mesmo (as assim chamadas bobinas de campo).
O torque sofrido pelo dipolo puntual Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } imerso em um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } pode ser calculado como:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \tau = \vec m \times \vec B } [1]
onde novamente tem-se o produto vetorial presente. O torque assim calculado é um vetor que aponta ao longo do eixo de rotação do dipolo, sendo a rotação do mesmo e o sentido do torque relacionados pela regra da mão direita: posto o dedão em direção e sentido análogos ao do vetor torque, o movimento estabelecido ao fechar-se a mão fornece o sentido de rotação do dipolo imposto por este torque.
A figura ao lado representa a situação de uma espira percorrida por uma corrente i quando imersa em um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } . A espira é vista em corte transversal, mostrando-se na parte inferior esquerda a seção do condutor solicitado pela corrente i entrando no papel (ou tela), e na parte superior direita a seção do condutor solicitado pela mesma corrente i, contudo agora já orientada de forma a sair do papel. Veem-se também as forças magnéticas que atuam nas respectivas seções dos condutores, o dipolo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } associado à espira como um todo, e ao centro, o torque resultante - um vetor perpendicular à tela, saindo dessa. A espira tende a girar em sentido anti-horário, de forma a alinhar os vetores ::Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } .
Interessante é perceber que, embora sujeito a um torque quando devidamente orientado em um campo magnético uniforme, a força resultante sobre o dipolo magnético é, em tal caso, visto que tem-se um binário de forças atuando sobre o mesmo, nula. Não observar-se-á translação do dipolo em virtude de forças magnéticas que nele atuem quando este estiver inicialmente estático em ambiente sujeito a um campo magnético uniforme. Um pequeno ímã no interior de um grande solenoide não trasladará sob ação das forças magnéticas que nele atuam. Contudo, caso o dipolo encontre-se em uma região do espaço onde o campo mostre-se não uniforme, este poderá ser solicitado por uma força magnética resultante. Tal situação encontra-se, a exemplo, quando um pequeno ímã é atraído - ou dependendo da orientação, repelido - em direção à região polar de um outro ímã obrigatoriamente não muito maior. Em tais casos é possível demonstrar-se que há uma resultante de forças atuando no dipolo, podendo esta ser determinada pela expressão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F = \nabla (\vec m . \vec B) } [1][22]
Trata-se pois do gradiente do produto escalar entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } . Ver-se-á que este produto escalar relaciona-se à energia potencial associada à posição e orientação do dipolo quando imerso no campo no referido campo magnético.
Motores elétricos

A figura "Motor elétrico" ao lado mostra uma aplicação prática do torque resultante sobre uma espira. Trata-se de um motor de corrente contínua. Ao centro, montado sobre o eixo em suportes específicos, encontram-se as três bobinas responsáveis por gerar os momentos de dipolo magnéticos, orientado cada qual em sentido perpendicular à respectiva face visível do suporte. Juntos, o eixo e estas três bobinas integram o rotor. Utilizam-se várias espiras aninhadas em uma formação conhecida como bobina pois desta forma seus seus momentos de dipolo magnéticos se somam, resultando em um torque de maior intensidade. O uso de várias bobinas, no caso três, tem a mesma finalidade. Na parte inferior, conectado a duas peças metálicas simetricamente opostas, um bobina fixa (a bobina de campo) é responsável por produzir o campo no qual as bobinas do rotor serão imersas. As peças metálicas são ferromagnéticas e com tais estabelece-se a configuração desejada do campo magnético, sendo este aproximadamente horizontal na região onde encontram-se as bobinas do rotor. Encontram-se também visíveis tanto o comutador (coletor e escovas) bem como os bornes para a ligação do aparelho a uma fonte de corrente elétrica externa responsável pela alimentação do mesmo. O comutador é necessário para manter o torque sempre em mesmo sentido. Ele alterna as bobinas de forma a manter aquela(s) com o torque em sentido desejado sempre ligada(s) e a(s) que estaria(m) implicando torque em sentido contrário desligadas. Sem ele, em vez de girar, o rotor tenderia a oscilar em torno do ponto no qual o momento de dipolo magnético de uma de suas bobinas alinha-se com o campo magnético oriundo da bobina de campo.
Os princípios de funcionamento envolvidos em motores de corrente alternada costumam ser mais elaborados, havendo casos em que as bobinas do rotor bem como o comutador que as alimenta são completamente eliminados. O rotor constitui-se então por peça metálica condutora única (não magnética), e correntes são nele estabelecidas através do processo de indução magnética. Contudo a ideia central permanece a mesma: um torque de origem magnética faz o rotor girar.
Lei de Biot-Savart
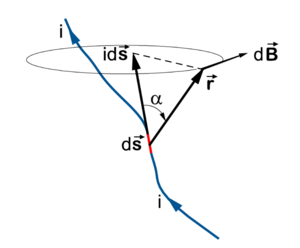
Correntes elétricas são a fonte primária de campos magnéticos. É certamente necessário pois que, dada uma distribuição de correntes conhecida, se possa calcular o campo magnético por ela produzido em um determinado ponto escolhido do espaço ao seu redor. A resposta a esta questão é fornecida pela lei de Biot-Savart.
Assumindo, sem perda de generalidade, que a distribuição de correntes seja representada por um condutor elétrico de espessura desprezível qualquer, e que esteja a transportar um corrente elétrica de intensidade i, dividindo-se este em infinitas seções de comprimento infinitesimal ds, cada seção devidamente representada e orientada por um diferencial de caminho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {ds} } , é possível associar-se a cada uma de suas seções um elemento de corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \vec {ds} } definido pelo produto entre o diferencial de caminho que representa a seção e a intensidade da corrente i que esta transportada. O elemento de corrente é pois um vetor tangente ao condutor no ponto em que este é definido.
Dado um elemento de corrente específico, este elemento de corrente certamente produz no espaço ao seu redor um campo magnético. O diferencial de campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dB} } que este elemento de corrente produz em um ponto do espaço situado a uma distância r deste segundo uma direção e sentido estabelecidos pelo vetor unitário Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {u_r} = \vec r / r } é, segundo a lei de Biot-Savart, calculado por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \vec B = k \frac {i \vec {ds} \times \vec {u_r}} {r^2} = k \frac {i \vec {ds} \times \vec r} {r^3}} [1]
Repare que o vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r } presente na lei de Biot-Savart localiza um dado ponto do espaço onde calcula-se o campo em relação ao elemento de corrente que o produz, e não em relação à origem do sistema de coordenadas. Trata-se pois do negativo do vetor que localiza o elemento de corrente em relação ao ponto onde calcula-se o campo, e não em relação à origem do sistema de coordenadas, salvo caso onde os dois pontos coincidam.
A constante de proporcionalidade k presente na lei de Biot-Savart depende do meio no qual encontram-se imersos a distribuição de correntes e o ponto onde calcula-se o campo. Essa constante relaciona-se com a permeabilidade magnética do meio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu } através da expressão:
- k = Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\frac {\mu}{4 \pi}) }
cujo valor é, para o vácuo:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = k_0 = 1 \times 10^{-7} T.m / A }
A permeabilidade magnética do vácuo é, como espera-se:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0 = 4 \pi \times 10^{-7} T.m / A }

Sabendo-se o campo magnético produzido por cada elemento de corrente em um dado ponto do espaço, pode-se calcular o campo magnético total neste ponto somando-se, ou seja, integrando, as contribuições de todos os elementos de corrente associados à distribuição de correntes dada:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \frac {\mu} {4\pi} \int {d \vec B} = \frac {\mu} {4\pi} \int {\frac {i \vec {ds} \times \vec {u_r}} {r ^2}} = \frac {\mu} {4\pi} \int {\frac {i \vec {ds} \times \vec {r}} {r^3}} } [1]
Há inúmeros exemplos de aplicações da Lei de Biot-Savart apresentados na literatura.[1][22] Exemplos podem também ser consultados no artigo específico sobre o assunto nessa própria enciclopédia.
A "Lei de Coulomb magnética"
A lei de Biot-Savart iguala-se à lei de Coulomb para o caso elétrico ao considerar-se que o diferencial de força magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dF} } que atua sobre o elemento de corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i' \vec {ds'} } quando em um ponto onde há um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } é dada por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dF} = i' \vec{ds'} \times \vec B } [1]
Nestes termos, em vista da lei de Biot-Savart, a força existente entre dois elementos de corrente devido apenas à interação magnética entre os mesmos vale:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dF} = \frac {\mu}{4 \pi} . \frac {i' \vec {ds'} \times i \vec {ds} \times \vec {u_r}} {r^2}}
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {u_r} } é um vetor unitário apontando do elemento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \vec {ds} } para o elemento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i' \vec {ds'} } , e r representa o valor da distância entre eles.
Embora não diretamente análoga à expressão da lei de Coulomb visto que tem-se na presente expressão um duplo produto vetorial e não produtos escalares, a semelhança entre as duas é evidente: a força magnética entre dois elementos de corrente decai, da mesma forma que a força elétrica entre duas cargas, com o quadrado da distância que os separa. Quanto à aplicação, há de se lembrar que, ao contrário das cargas elétricas, que podem existir e existem como entidades puntuais, um elemento de corrente não existe isolado, havendo em geral um circuito de corrente a ser considerado - no qual o elemento de corrente representa apenas uma diminuta parte. Assim, uma integral - em verdade duas integrais - fazem-se necessárias ao se calcular a força magnética entre dois destes circuitos: uma para determinar-se o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{(\vec r)} } existente em cada ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r } do espaço devido ao primeiro circuito (o circuito sem " ' ") - a integral descrita acima - e outra para se determinar a força resultante sobre o segundo circuito (o circuito " ' "):
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F = \int \vec {dF} = \int i' \vec{ds'} \times \vec B_{(\vec r)} }
Na maioria dos casos estas integrais mostram-se certamente laboriosas de se fazer, contudo, da mesma forma que a existência de simetria facilita em muito as soluções dos problemas associados no caso elétrico - a citar-se as aplicações da Lei de Gauss como exemplo - a existência de simetria tanto no circuito fonte do campo magnético como no circuito sob influência deste pode igualmente ser, e geralmente é, explorada de forma a simplificar em muito as soluções dos problemas correlatos.
Ferramenta indispensável em tal processo, a Lei de Ampère para o caso magnético desempenha papel semelhante ao da Lei de Gauss para no caso elétrico.
Leis de Ampère e Gauss

No estudo do eletromagnetismo e em suas subáreas são particularmente importantes como ferramentas dois teoremas oriundos do cálculo integral e diferencial - teoremas em particular ligados ao cálculo vetorial - respectivamente nomeados Teorema de StokesPredefinição:Nota de rodapé e de Teorema de Gauss. Estes teoremas basicamente relacionam a integral (ou seja, a "soma") de uma dada grandeza "bem comportada" ao longo da fronteira que delimita uma dada região fechada do espaço considerado e a integral de uma segunda grandeza presente na região interna à fronteira e por essa definida. Se o espaço a se considerar é uma superfície, a fronteira é uma linha curva fechada que forma a borda da região por ela demarcada e tem-se em tal caso o teorema de Stokes: uma integral de caminho de uma dada grandeza ao longo do perímetro mostra-se proporcional a uma integral de superfície de uma segunda grandeza ao longo da área da região definida por esta fronteira. Se a região em questão consiste em um volume tridimensional, a fronteira é uma superfície fechada imersa no espaço tridimensional, e associado tem-se então o teorema de Gauss: uma integral de superfície de uma grandeza ao longo da fronteira mostra-se proporcional a uma integral de volume de uma segunda grandeza ao longo de todo o espaço tridimensional confinado.
As duas grandezas consideradas anteriormente certamente não podem ser escolhidas a esmo, devendo as mesmas satisfazerem a certas condições bem definidas, e certamente encontram-se relacionadas entre si, pois com a aplicação de tais teoremas pretende-se justamente determinar tal relação.Predefinição:Nota de rodapé Ambos os teoremas têm suas aplicações tanto em eletrostática quanto em magnetostática, e também estão notoriamente presentes nas equações de Maxwell para o eletromagnetismo.
A Lei de Ampère para a magnetostática consiste basicamente na aplicação do teorema de Stokes para o caso em que a grandeza integrada na fronteira é o vetor campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } , e a grandeza integrada ao longo da superfície é a densidade superficial de corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec j } .
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \oint_{perim.} \vec B \vec {dl} = \mu_0 \int_{sup.} \vec j \vec {da} = \mu_0 I_{enc.}} [1][22]
A densidade superficial de corrente simplesmente mede a quantidade de carga elétrica (em coulombs) que atravessa um diferencial de área Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {da} } (cuja unidade é o metro quadrado) por unidade de tempo (medido em segundos), ou seja, o corrente (em ampères) que flui em direção perpendicular - de forma a atravessar - à superfície da área infinitesimal considerada. Esta integral, conforme percebe-se, dá por resultado a corrente total que flui através da área encerrada pela fronteira, uma vez que soma as correntes por diferencial de área ao longo de todos os diferenciais de área na qual se divide a superfície em questão.
A integral do campo magnético ao longo do caminho simplesmente projeta o campo magnético em cada ponto da fronteira na direção paralela à fronteira naquele ponto, ou seja, na direção do diferencial de caminho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dl} } que define a fronteira naquele ponto, e posteriormente soma o produto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_{(//)} dl } ao longo de uma volta completa na fronteira. Repare que a componente do campo magnético perpendicular à fronteira no ponto não é considerada, e que o resultado desta integral tem unidade equivalente à unidade de comprimento (associado ao diferencial de caminho e ao perímetro da região, em metros) multiplicado pela unidade de campo magnético (tesla).
A constante de proporcionalidade necessária para igualarem-se as integrais anteriores é, conforme visto, a permeabilidade magnética do meio - no caso o vácuo - já anteriormente considerada.

A comparação entre a forma integral da Lei de Ampère acima e a integral presente no teorema fundamental para o rotacional
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{sup.} (\nabla \times \vec v) . \vec {da} = \oint_{perim.} \vec v . \vec {dl} } [22]
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec v } representa um campo vetorial genérico a se considerar leva ao fato de que:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{sup.} (\nabla \times \vec B) . \vec {da} = \oint_{perim.} \vec B \vec {dl} = \int_{sup.} (\mu_0 \vec j) \vec {da} } [22]
onde a primeira e a última integrais podem ser comparadas diretamente. Desta comparação resulta:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec {B} = \mu_0 \vec {j} } [22]
Em resumo tem-se que rotacional de um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } em torno de um ponto é proporcional à densidade de corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec j } naquele ponto. Tal ideia tornar-se-á clara ao se considerar o exemplo na seção seguinte no qual determina-se o campo magnético ao redor de um fio retilíneo longo conduzindo uma corrente elétrica I.
Também é importante neste e demais exemplos que se seguem perceber que a Lei de Biot-Savart e de Ampère também implicam que o divergente do campo magnético seja sempre zero,[22] de modo que as linhas de campo magnéticas - que representam o campo magnético, um campo vetorial - são sempre linhas fechadas, e nunca têm - de forma diferente das linhas de campo elétrico - origem e término em pontos distintos do espaço. Trata-se pois da Lei de Gauss aplicada ao magnetismo, que relaciona a integral de superfície do campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } ao longo de uma superfície fechada com a integral da densidade de carga magnética no volume interno à superfície, ou seja, com a carga magnética total imersa no respectivo volume. Afirma basicamente que não há monopolos magnéticos (cargas magnéticas), de forma que a primeira integral deve igualar-se a zero pois a segunda empiricamente o é.
Em vista dos teoremas da divergência e do rotacional, para campos magnetostáticos, em suas respectivas formas diferenciais:
- Lei de Gauss: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \vec B = 0 } [22]
- Lei de Ampère: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec {B} = \mu_0 \vec {j} } [22]
As mesmas leis em suas respectivas formas integrais se tornam:
- Lei de Gauss: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \oint_{sup.} \vec B \vec {da} = 0} [1][22]
- Lei de Ampère: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \oint_{perim.} \vec B \vec {dl} = \mu_0 \int_{sup.} \vec j \vec {da} = \mu_0 I_{enc.}} [1][22]
Um pouco mais além

James Clerk Maxwell expandiu a Lei de Ampère para os casos envolvendo campos elétricos variáveis basicamente afirmando que campos elétricos variáveis também criam, assim como correntes, campos magnéticos, e que por tal influem no resultado da integral de linha do campo magnético ao longo do circuito de ampère caso haja no interior deste circuito um campo elétrico variando no tempo.
A título de ilustração apenas - por estar fora do escopo do presente artigo - para campos eletromagnéticos as leis de Ampère com a correção de Maxwell e a Lei de Gauss são, respectivamente:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec B = \mu_0 \vec j + \mu_0 \epsilon_0 \frac {\partial \vec E}{\partial t} } [22]
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \vec B = 0 } [22]
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_0 } representa a permissividade elétrica do vácuo, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec E } representa o campo elétrico, "t" representa o tempo, e a correção de Maxwell é expressa em termos de derivada parcial do campo elétrico em relação ao tempo.
Maiores detalhes podem ser obtidos pesquisando-se as Equações de Maxwell para o eletromagnetismo.
Andando em círculos
Tanto a lei de Biot-Savart quanto a Lei de Ampère encerram em si as mesmas informações, e são, por tal, equivalentes. Partindo-se de uma é possível, após alguns cálculos matemáticos, obter-se a outra. O uso de uma ou outra depende da situação. A Lei de Ampère talvez seja a mais conhecida e aplicada em virtude desta mostrar-se muito útil e simples em situações onde a simetria envolvida colabora, e por ser esta a forma a figurar nas famosas equações de Maxwell. Ver-se-á em seguida a aplicação da mesma a alguns casos específicos de importância prática relevante, contudo a solução em vista da Lei de Biot-Savart também é plenamente acessível, sendo apresentada com frequência na literatura.[1][22]
O campo magnético e o fio retilíneo

O exemplo mais comum da aplicação da Lei de Àmpere presente na literatura refere-se certamente à determinação do campo magnético ao redor de um fio retilíneo suficientemente longo ("infinito") conduzindo uma corrente elétrica I.[1][22] Sua solução começa por escolher-se o circuito de ampère, um caminho imaginário circundando o fio que, conforme sugerido pela simetria inerente ao problema, é sempre escolhido como uma circunferência inscrita em um plano que seja perpendicular ao fio, com o fio ao centro desta. Tal escolha acarreta consideráveis simplificações nos cálculos visto que é esperado que o campo magnético tenha tal configuração em torno do fio tanto por razões práticas quanto por razões teóricas: a densidade de corrente neste caso confina-se ao centro da circunferência, sendo perpendicular ao plano que contém esta última; logo, o rotacional do campo deve ser proporcional à mesma, o que implica que o campo magnético deve "girar" em torno do fio conforme orientação dada mais uma vez pela regra da mão direita, estando o vetor campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } sempre contido no plano em questão. Por razões de simetria o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } será o mesmo sobre qualquer ponto da circunferência. Acrescendo-se considerações sobre as propriedades do campo magnético, não espera-se que haja componente do campo magnético perpendicular ao circuito de ampère, ou seja, em direção radial, o mesmo aplicando-se para componente em direção axial (ou seja, paralela ao fio).
Nestes termos tem-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } paralelo ao diferencial de caminho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dl} } , sendo este último, em virtude de sua definição, também tangente à circunferência. O produto vetorial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B .\vec dl } reduz-se ao produto escalar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B .dl } pois Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dl} } são paralelos e B tem o mesmo valor ao longo de todos os pontos da circunferência de ampère escolhida - cujo raio vale r. Tem-se pois que a integral de caminho vale:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \oint_{perim.} \vec B . \vec {dl} = \int B.dl = B \int dl = 2 \pi r B }
onde a integral do diferencial de caminho dl ao longo do perímetro resulta obviamente no perímetro da circunferência, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C = 2 \pi r } . Tal integral deve, segundo a Lei de Ampère, igualar-se à Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0 I_{Encer.} } , donde tem-se que:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \pi r B = \mu_0 I } , o que implica:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B = \frac {\mu_0 I} {2 \pi r} } [1]
Que é a expressão que permite o cálculo do valor do campo magnético B a uma distância R do fio que conduz a corrente I. Em coordenadas cilíndricas tem-se pois que:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \frac {\mu_0 I} {2 \pi r} \vec {u_ { \theta}} } [22]
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {u_ { \theta}} } é um vetor unitário perpendicular ao eixo z (ao fio) e à direção radial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {u_ {r}} }
O campo magnético e o toroide

Um toroide consiste e um anel circular estilo "rosquinha de coco" em torno do qual enrola-se um longo fio condutor, obedecendo para tal sua geometria (ver figura). Nesse exemplo as espiras são uniformemente espaçadas e densas o suficiente para que o campo no interior do toroide possa ser considerado uniforme e para que cada espira possa ser considerada por si só um circuito de corrente fechado. O toroide tem núcleo de ar, o que será aproximado por vácuo.
Escolhendo-se um circuito de ampère circular que acompanhe a anatomia do toroide contudo interno a este, tem-se que a solução da integral de linha mostra-se análoga à do caso do fio retilíneo, com a diferença de que a corrente I conduzida pelo fio passa agora N vezes através da superfície delimitada pelo circuito de ampère, sempre em mesma direção - na região central do toroide. Repare que a corrente externa ao circuito de ampère - sobre o perímetro externo do toroide - não entra em consideração, tão pouco as correntes paralelas ao circuito de ampère - nas partes superior e inferior do toroide - pois estas não "furam" a superfície delimitada pelo circuito de ampère. Assim, para um toroide de raio interno "a" e raio externo "b" tem-se:[22]
- r < a : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } = vetor nulo
- a < r < b : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \frac {\mu_0 NI} {2 \pi r} \vec {u_ { \theta}} } [1][22]
- r > b : Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } = vetor nulo
onde N representa o número de espiras do toroide e r representa a distância do ponto onde se determina o campo até o eixo de simetria (centro) do toroide.
Vale ressaltar que esse é o campo para um toroide com espiras compactas e núcleo de ar. O campo magnético no interior do toroide com núcleo material é devido não apenas à corrente nas espiras como também à magnetização induzida no material que compõe o seu núcleo. Nesse caso a Lei de Ampère permite o cálculo não do campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B} propriamente ditoPredefinição:Nota de rodapé mas sim o de um campo auxiliar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H} - sendo esse e não o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B} por vezes nomeado campo magnético por alguns autores.
Ao campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } reserva-se então outros nomes tais como "densidade de fluxo magnético" ou "indução magnética" - fato que gera por certo recorrente confusão quanto às designaçõesPredefinição:Nota de rodapéPredefinição:Nota de rodapé Esse campo auxiliar, aqui nomeado "campo excitante", "estímulo magnético", "estimulação magnética", ou simplesmente campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H} , desempenha papel importante na magnetostática, e será abordado mais adiante.
O campo magnético e o solenoide

Um solenoide consiste em uma hélice de fio com extremos conectados a uma fonte de corrente elétrica. Tratar-se-á aqui de um solenoide bem longo com espiras compactas, e determinar-se-á o campo nas regiões internas e distantes dos extremos do mesmo.
Imaginando-se um circuito de ampère retangular inscrito em um plano que contenha o eixo do solenoide e posicionado de forma a envolver um número significativo nL espiras deste solenoide em uma região próxima ao seu centro axial, desenhado de forma a ter-se um dos lados deste circuito de ampère interno e o outro externo ao solenoide, tem-se que a integral de linha ao se percorrer este circuito mostrar-se-á igual a B multiplicado pelo comprimento (e não pelo perímetro) L deste circuito. Aqui n representa o número de espiras por unidade de comprimento do solenoide, de forma que nL representa o número de espiras confinado no circuito de ampère em questão. Tem-se também que a espessura deste circuito pode ser desprezada visto que pode ser feita tão pequena quanto se queira, o que significa em termos práticos assumir-se um fio com espessura desprezível perto ao comprimento L escolhido para o cálculo. Para tal cálculo usou-se que o campo magnético de um solenoide "infinito" deve mostra-se paralelo ao seu eixo tanto interna quanto externamente, e que em verdade o valor do campo B do lado externo do solenoide "infinito" é igual a zero, fatos plenamente justificados em virtude da simetria envolvida.[1][22] Nesses termos:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \oint \vec B \vec {dl} = BL = \mu_0 I_{Encer.} = \mu_0 (nL)i } [1]
O que resulta em:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B = \mu_0 n i} [1]
onde n é representa o número de espiras por unidade de comprimento do solenoide e i representa a corrente transportada pelo fio deste.
O campo em regiões internas próximas ao centro axial de um solenoide é, conforme determinado, uniforme tanto em módulo como em direção e sentido, o que o torna um significativo instrumento no estudo e aplicações da magnetostática quando há necessidade de se produzir campos magnéticos dessa natureza. Nos aparelhos de ressonância magnética nuclear, a exemplo, tem-se um potente solenoide envolvendo a amostra ou paciente sob exame.
Fluxo magnético e indutância
Contando as linhas de campo
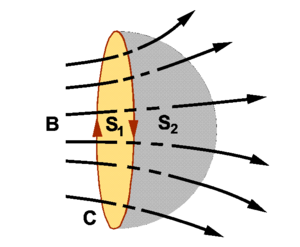
Conforme visto, a Lei de Gauss aplicada ao magnetismo estabelece que a integral de superfície do campo magnético sobre uma área fechada vale zero. Conduto pode-se pensar na mesma integral em áreas abertas, sendo a mesma então uma equação constitutiva para uma grandeza escalar nomeada fluxo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi } :
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi = \int \vec B \vec {da} }
A unidade de fluxo magnético é, pois, dada pelo produto entre as unidades das grandezas envolvidas, ou seja, entre a unidade de campo magnético e a unidade de área. No Sistema Internacional de Unidades, o fluxo mede-se em weber, em clara homenagem ao físico Wilhelm Eduard Weber.
- [Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi } ] = weber = tesla metro quadrado = Wb = T.m²
A Lei de Gauss pois afirma que o fluxo magnético através de qualquer superfície fechada é nulo.
Para superfícies abertas em regiões onde haja um campo unidirecional, o fluxo é tanto maior quanto maior o campo magnético onde esta se encontra, e tanto maior quanto maior a área determinada por seu perímetro. A orientação entre a superfície e o campo mostra-se também importante: dada uma área plana A, o fluxo será máximo quando a superfície estiver orientada de forma perpendicular ao campo magnético (ou seja, com o vetor área paralelo ao campo), e será nulo caso a superfície mostre-se paralela ao campo (ou seja, com o vetor área perpendicular ao campo). Para superfícies planas imersas em campos uniformes a integral anterior resulta:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi = B A cos (\theta) }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } representa o ângulo entre o vetor área e o campo magnético em questão.
Assumida uma representação do campo através de linhas de campo, pode-se simploriamente entender o fluxo como uma grandeza diretamente proporcional ao número líquido de linhas da representação que "furaram" a superfície considerada em um dado sentido, ressaltado por tal o fato que uma linha passando através desta superfície em um sentido "contrário" ao definido como positivo "cancela" uma linha passando em sentido favorável.

Assumindo-se uma região de campo uniforme e uma área plana cujo fluxo não se mostre inicialmente nulo, aumentando-se a área desta superfície espera-se que o número liquido de linhas aumente, e por tal também o fluxo. Caso o campo torne-se mais intenso, este deverá ser representado por uma densidade maior de linhas, o que também acarreta aumento no número de linhas que furam uma mesma área na representação considerada, e por tal um aumento no fluxo. Mesmo mantendo-se a área e o campo constantes pode-se também fazer o fluxo variar, bastando para tal girar a área em torno de um eixo nesta contido e adequadamente escolhido de forma que este se mostre perpendicular ao campo magnético na região. Em essência, isto significa fazer o ângulo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } entre o vetor área e o campo variar, e por tal também o fluxo. Tal mecanismo de variação de fluxo é o que se encontra presente nos geradores de eletricidade uma vez que é requerida, em acordo com a Lei de Faraday, uma constante variação de fluxo para o funcionamento adequado dos mesmos.
Uma questão de geometria

Uma segunda grandeza física estabelecida com base no conceito de fluxo é a indutância. A indutância relaciona o fluxo magnético produzido por um circuito elétrico em uma superfície especificada e a corrente elétrica I que se faz circular através do circuito elétrico em questão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind. = \frac {\Phi} {I} }
A indutância é uma grandeza física cujo valor depende apenas da geometria do circuito ou circuitos envolvidos, ou seja, trata-se de uma grandeza atrelada apenas à configuração espacial do sistema.
Há pois como se definir duas indutâncias: a autoindutância, que corresponde ao fluxo através da área delimitada por um circuito elétrico quando uma corrente I percorre esse próprio circuito, e a indutância mútua, que relaciona o fluxo através de um circuito elétrico secundário quando faz-se uma corrente elétrica I circular através do circuito elétrico primário.
A autoindutância de um solenoide de comprimento L e raio R, assumido L muito maior que R, é fácil de ser determinada visto que o campo em seu interior é constante. O fluxo através da área interna total associada às nL espiras do solenoide, cada espira representando uma área de seção reta Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi R^2 } é, pois:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi = B.A = (\mu_0 n I).(nL \pi R^2) }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi = B.A = \pi \mu_0 n^2 L I R^2 }
onde n representa, conforme antes discutido, a densidade linear de espiras do solenoide, e nL o número total de espiras do mesmo. A autoindutância do mesmo é:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{solen.}= \frac {\Phi} { I }= \pi \mu_0 n^2 L R^2 } [22]
Repare que a indutância Ind.Predefinição:Nota de rodapé depende apenas de grandezas associadas à geometria do solenoide: da densidade de espiras, ou seja, do número de espiras por unidade de comprimento n; do próprio comprimento L, do número total de espiras nL; do raio R do solenoide e do material presente em seu núcleo - no caso nenhum (vácuo) - situação adequadamente representada mediante a presença da constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0 } na expressão associada.

A indutância mútua é muito explorada em um dispositivo conhecido por transformador. O transformador mais simples que existe constitui-se por dois solenoides, um com raio r e outro com raio maior R, enrolados um interno ao outro com seus eixos se sobrepondo. Designando-se o circuito primário por circuito 1 e o circuito secundário por circuito 2, e com a condição de que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1 >> L_2 >> R } , vê-se que o fluxo através da superfície total determinada pelas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_2L_2 } espiras do solenoide interno quando o solenoide externo é percorrido por uma corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1 } é:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12} = B_1 . (n_2L_2)A_2 = \mu_0 n_1 I_1 . n_2 L_2 \pi r^2 }
de forma que a indutância mútua Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind_{12} } do solenoide de raio R atuando como circuito primário e do solenoide de raio r atuando como circuito secundário (através do qual o primário estabelece o fluxo) é:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{12} = \frac {\Phi_{12}} {I_1} = \mu_0 \pi r^2 n_1 n_2L_2 } [22]
que, novamente, depende apenas de grandezas geométricas envolvendo a configuração dos circuitos primário e secundário. Pode-se agora perguntar qual será a indutância mútua do circuito secundário sobre o circuito primário, ou seja, qual a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{21} } associada aos circuitos em questão. A resposta é obtida ao considerar-se a equação fundamental para o cálculo de qualquer indutância a partir das geometrias dos circuitos fechados envolvidos:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{12} = \frac {\mu_0}{4 \pi} \oint \oint \frac {\vec {dl_1} \vec {dl_2}}{ | \vec {r_1} - \vec {r_2} | } } [22]
Observando-se esta equação, conhecida como Fórmula de Neumann, vê-se que a indutância depende novamente apenas da geometria do sistema formado pelos dois circuitos, e que esses foram divididos em pedaços infinitesimais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dl_1} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dl_2} } a fim de calcular-se a "relação mútua" entre cada par de partes infinitesimais e posteriormente somar-se tudo - mediante a dupla integral - a fim de se obter a indutância mútua dos circuitos. Pode-se responder a questão anterior observando-se que a troca de papéis entre os circuitos 1 e 2 é completamente simétrica, de modo que:
| “ | Quaisquer que sejam as formas e as posições dos anéis de corrente, o fluxo através do circuito 2, quando se faz fluir uma corrente I através do circuito 1, é idêntico ao fluxo através do circuito 1 quando se impõe a mesma corrente I ao circuito 2. | ” |
ou seja, a indutância mútua Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind_{12} } é sempre igual à indutância mútua Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{21} } .
Repare que a equação para a autoindutância de um solenoide pode ser obtida fazendo-se o circuito primário e secundário coincidentes, ou seja, supondo-se que ambos são o mesmo circuito.

Das equações acima conclui-se que as unidades tanto da autoindutância quanto da indutância mútua devem corresponder à unidade da constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0 ::} multiplicada por uma unidade de comprimento. Tem-se pois:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [Ind.] = \frac {tesla.metro}{ampere}. metro = \frac {T.m}{A} . m = \frac {T m^2}{A} = henry }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [Ind.] = henry = \frac {tesla.metro^2}{ampere} } , ou seja, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1H = 1 \frac {Tm^2} {A} }
Indutores típicos empregados em eletrônica têm indutâncias que variam de uns poucos microhenrys a alguns milihenrys, e normalmente não têm núcleos de ar. Para indutores com núcleos maciços tem-se que fazer uma correções associada às propriedades magnéticas dos materiais em seus núcleos, que, devido à magnetização, geralmente intensificam o valor do campo magnético no interior desses componentes. Deve-se para tal fazer uma correção através da permeabilidade relativa, ou seja, deve-se usar a permeabilidade magnética absoluta do material e não a do vácuo nas referidas equações para o cálculo da indutância.
A título de ilustração cita-se a indutância de um toroide retangular de raio interno a, raio externo b, altura h, formado por N voltas de fio sobre um núcleo material cuja permeabilidade absoluta Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = k_m \mu_0 } é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_m } vezes a permeabilidade do vácuo.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{Toroide} = k_m (\frac {\mu_0N^2h}{2 \pi} ln \frac {b}{a}) } [1]
A indutância de um componente com núcleo material é proporcional à indutância do mesmo componente sem núcleo material. A constante de proporcionalidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_m } é a permeabilidade relativa do material, por vezes também nomeada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_r } .
Um pouco mais além
A Lei da Indução de Faraday estabelece que a variação do fluxo magnético em um circuito é responsável pela indução de uma tensão elétrica nesse, sendo essa tanto maior quanto maior for a taxa com que o fluxo varia. Tem-se tal comportamento expresso via equação:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Epsilon = \frac {d \Phi}{dt} }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Epsilon } representa a tensão elétrica verificada ao longo do perímetro que define a área a qual associa-se o fluxo magnético em questão.
A mesma lei figura nas Equações de Maxwell, em sua forma integral, como se segue.[25]
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \oint_{perim.} \vec E \cdot \vec {dl} = -\frac { \partial \Phi_{sup.} }{ \partial t} }
Na forma diferencial essa traduz-se por:[25]
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec E = -\frac { \partial \vec B}{ \partial t} }
A Lei da Indução de Faraday justifica o uso quase que obrigatório de correntes alternadas ou variáveis ao se lidar com transformadores ou indutores: só há tensão e corrente elétricas induzidas no circuito secundário caso o fluxo através do mesmo esteja a variar, e em tais componentes o fluxo através do secundário varia quando a corrente através do circuito primário é feita variável. O conceito de autoindução faz com que o mesmo raciocínio aplique-se também aos indutores.
Visto que o campo elétrico induzido pela variação do fluxo não se mostra conservativo, considerações importantes quanto a esta lei atrelam-se à energia envolvida no processo e à sua conservação. Aparte o afrente abordado, este assunto foge ao escopo desse artigo e não será por tal aqui discutido. Pormenores sobre o assunto encontram-se contudo disponíveis e bem descritos no âmbito do eletromagnetismo.
Lado a lado com a corrente
Um conceito amplamente difundido no estudo dos fenômenos envolvendo campos elétricos conservativos é o conceito de potencial elétrico - especificamente, o conceito de tensão elétrica. A ideia intuitiva de se estabelecer raciocínio análogo para os fenômenos magnéticos não se mostra, entretanto, tão imediata. Em vista de o campo magnético, salvo em sistemas muito específicos, não admitir um potencial escalar para descrevê-lo, definir-se-á o então chamado "potencial magnético" como uma grandeza vetorial e não como uma grandeza escalar, e por tal este não admitirá um sentido físico tão explícito como o encontrado para o caso elétrico, o de energia associada à unidade de carga.
Mesmo sem um sentido físico diretamente expresso, o potencial magnético desempenha um papel de vital importância teórica para a compreensão dos fenômenos associados. Constitui também uma poderosa ferramenta prática para a soluções de problemas na área. Um domínio um pouco mais aprofundado sobre campos e álgebra vetoriais mostra-se, contudo, necessário. A compreensão das subseções que se seguem requer também familiaridade com operadores lineares tais como gradiente, divergente, rotacional e laplaciano.
Sobre potenciais e campos vetoriais
Na teoria dos campos vetoriais encontra-se o Teorema de Helmholtz, que em sua essência afirma: "Dadas as condições de contorno adequadas, um campo vetorial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec Z_{(\vec r)} } é univocamente determinado uma vez conhecidos seu divergente e seu rotacional".[22] Tem-se em verdade
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec Z_{(r)} = - \nabla V_{(r)} + \nabla \times \vec A_{(r)} }
que se traduz-se por:
| “ | Um campo vetorial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{(\vec r)} } bem comportado pode sempre ser expresso como o gradiente de um campo escalar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{(r)} } mais o rotacional de um segundo campo vetorial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A_{(\vec r)} } . | ” |
Condições de contorno adequadas estão geralmente presentes no estudo da eletrostática e magnetostática de tal forma que os campos elétricos e magnéticos associados usualmente são expressos também em função de rotacionais e divergentes de seus respectivos campos potenciais. Considerável simplificação é neste caso observada - tanto em magnetostática quanto em eletrostática - dado o fato que o campo eletrostático é sempre irrotacional e o campo magnetostático é sempre um campo não divergente:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \vec B = 0 }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec E = 0 } .
Nesses termos o campo elétrico Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec E } pode ser expresso apenas como o divergente de um campo escalar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V{(\vec r)} } visto que o rotacional do divergente de um campo escalar é sempre nulo. Tem-se pois que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{(\vec r)}} , um campo escalar e não vetorial, carrega em si todas as informações relativas ao campo elétrico associado, o que leva diretamente ao conceito de potencial elétrico e ao conceito de tensão ou diferença de potencial elétricos:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec E_{(\vec r)} = - \nabla . V_{(\vec r)} } .
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec E = \nabla \times (- \nabla . V_{(\vec r)}) = 0 }
De forma similar tem-se a condição de que um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } pode ser expresso como o rotacional de um campo vetorial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } visto que o divergente do rotacional é sempre nulo.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{(\vec r)} = \nabla \times A_{(\vec r)} } .
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \vec B_{(\vec r)} = \nabla . (\nabla \times A_{(\vec r)}) = 0 }
O potencial magnético

O campo vetorial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } acima definido é conhecido como potencial magnético, desempenhado não de forma tão simples - visto que trata-se de um campo vetorial e não escalar - um papel em muito similar ao papel que o potencial elétrico desempenha no caso da eletrostática.
É de relevância pontuar-se aqui que o conhecimento do campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } define qual deve ser o rotacional do campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } , contudo nada diz a respeito da divergência deste último. Há assim vários campos vetoriais Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } que diferem entre si por parcelas associadas a campos não rotacionais quaisquer que, contudo, representam igualmente bem o campo magnético em questão. Como exemplo, todos os campos derivados de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } mediante uma transformação de gauge
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A => \vec A + \nabla \psi } [24]
- onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi } é um campo escalar qualquer - são aceitáveis como campos potenciais para o mesmo campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B} em questão visto ser o rotacional do divergente de uma função escalar sempre nulo.
Algo similar acontece em eletrostática: campos potenciais elétricos (escalares) que difiram entre si apenas pela soma ou subtração de um valor constante representam o em essência o mesmo campo elétrico. A escolha mais óbvia em ambos os casos é atribuir-se o valor zero à liberdade de escolha ofertada sempre que possível. Com a condição de que o campo potencial magnético seja escolhido como um campo rotacional puro, ou seja, que o potencial magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } seja escolhido de forma a ter divergente nulo, a Lei de Ampère, a rigor escrita como:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla ( \nabla . \vec A) - \nabla^2 \vec A = \mu_0 \vec j } [24]
se transforma em:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla ^2 . \vec A_{(\vec r)} = -\mu_0 \vec J } [22][24]
Ou seja, para vetores potenciais escolhidos de forma que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla. \vec A = 0 } o laplaciano do potencial magético é proporcional à densidade de corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec j } .
Assumindo-se que a densidade de corrente seja nula no infinito pode-se determinar o vetor potencial a partir da distribuição da densidade de corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec j } mediante a integral:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A_{(\vec r)}= \frac {\mu_0}{4 \pi} \int \frac { \vec j_{( \vec {r'})}}{| \vec r - \vec {r'}|} d^3r' } [22]
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^3r' } representa o elemento de volume, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {r'} } localiza a densidade de corrente em relação à origem do sistema de coordenadas, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {r} } localiza o ponto onde determina-se o potencial magnético em relação à origem do mesmo sistema, e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle | \vec r - \vec {r'}| } corresponde ao valor da distância entre os dois elementos anteriores.
É importante ressaltar que: "... uma vez que a força magnética não realiza trabalho, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } não admite uma interpretação física simples em termos de energia potencial por unidade de carga [elétrica]" como aquela associada ao potencial elétrico. "Em alguns contextos [específicos] ele pode ser interpretado como o momento por unidade de carga [elétrica]. Contudo, o vetor potencial tem substancial importância teórica...",[22] inclusive a ponto de merecer menção neste artigo, mesmo requerendo conhecimento mais aprofundado em cálculo vetorial.
A título de curiosidade cita-se alguns potenciais magnéticos em sistemas específicos. Solicita-se ao leitor que consulte a literatura quanto à matemática, não muito trivial, associada ao cálculo dos mesmos.
O potencial e o solenoide infinito
Para um solenoide infinito com n espiras por unidade de comprimento, raio R e corrente por espira I:[22]
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A = \frac {\mu_0nI}{2} r {\hat \phi} } para pontos internos ao solenoide (r < R).
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A = \frac {\mu_0nI}{2} \frac {R^2}{r} {\hat \phi} } para pontos externos ao solenoide (r > R).
Repare que o vetor potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } mostra-se "paralelo" à corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec j } no solenoide, ou seja, em quaisquer dois pontos radialmente conectados o vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } determinado pelo primeiro ponto e o vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec j } sobre o ponto da superfície do solenoide radialmente associado apontam sempre em mesma direção, neste caso em direção paralela à direção do vetor unitário Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {\hat \phi} } atrelado aos referidos pontos uma vez obedecidas as regras do sistema de coordenadas cilíndricas em consideração. O "paralelismo" entre os vetores potencial magnético e densidade de corrente é, aparte o sistema de coordenadas mais adequado, geralmente observado em todos os sistemas que exibam alta simetria, incluindo-se na pertinente lista não apenas o presente sistema mas também o sistema formado pela esfera girante com densidade superficial de carga uniforme discutido a seguir.
O potencial e a esfera girante
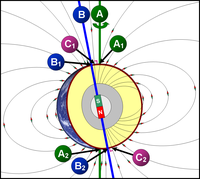
Para uma casca esférica de raio R carregada com densidade superficial de carga uniforme Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma } que gire com velocidade angular constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \omega } :[22][24]
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{(\vec r)} = \frac {\mu_0 R \sigma}{3} ( \vec \omega \times \vec r ) } para pontos no interior da esfera.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{(\vec r)} = \frac {\mu_0 R^4 \sigma}{3r^3} ( \vec \omega \times \vec r ) } para pontos exteriores à esfera a uma distância r de seu centro.
Curiosamente o campo magnético é uniforme dentro da esfera, o que, assumindo-se um sistema esférico de coordenadas com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \omega } coincidindo com o eixo Z:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \nabla \times \vec A = \frac {2 \mu_0 \sigma R \omega}{3} \hat z }
O magnetismo e a energia
Ao falar-se em energia potencial normalmente tem-se também em mente um campo de forças adequadamente associado, força essa responsável pela conversão da energia potencial em energia cinética (e vice-versa) quando o sistema sofre transformações espaciais que impliquem variação na primeira. A exemplo, associado à energia potencial gravitacional e ao campo gravitacional tem-se o campo de forças gravitacionais. Associado à energia potencial elétrica e ao campo elétrico tem-se o campo de forças elétricas.
Ao falar-se em energia magnética há contudo uma série de divergências significativas do raciocínio anteriormente exposto, a começar pelo fato de que, ao contrário das forças elétrica e gravitacional, a força magnética não realiza trabalho.
Sobre o ócio da força magnética

Parafraseando um pouco, a força magnética é por natureza um ente físico um tanto quanto ocioso visto que literalmente não trabalha. Tal argumento fundamenta-se na definição física de trabalho, diretamente relacionada à conversão ou transferência da energia associada ao movimento - a energia cinética. O diferencial de trabalho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec { d \Tau } } realizado por uma força Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F } é definido como o produto entre o diferencial de deslocamento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dl} } sofrido por um objeto e a componente da força que neste atua de forma paralela a este deslocamento, ou seja, como o produto entre o diferencial de deslocamento e a componente da força paralela à velocidade do objeto. Tem-se pois que o diferencial de trabalho corresponde ao produto escalar entre o vetor deslocamento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {dl} } e a força Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F } , e o trabalho total realizado sobre o objeto é a soma, ou seja, a integral, dos diferenciais de trabalho ao longo da trajetória em questão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Tau = \int \vec F \vec {dl} }
A título de curiosidade, diferenciando-se ambos os lados em relação ao tempo, tem-se que, para campos de força independentes do tempo, o produto escalar entre a força e a velocidade instantânea fornece a potência Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P } instantânea associada ao trabalho sendo realizado:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{(t)} = \vec F_{(t)}. \vec V_{(t)} }
Relembrando o fato de que a força magnética mostra-se sempre perpendicular à velocidade da carga elétrica q sob seu efeito - em função do produto vetorial entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec V } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } presente na equação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_M = q \vec V \times \vec B } - conclui-se que o produto escalar entre a força magnética e a velocidade, e por tal entre a força magnética e o diferencial de deslocamento, vetores sempre ortogonais, é sempre nulo. Logo, com tradução literal:
| “ | A força magnética não trabalha. | ” |
A força magnética não consegue, pois, alterar a energia cinética de uma carga em movimento, sendo capaz de alterar a velocidade dessa apenas no que se refira à sua direção e sentido. Forças magnéticas colocam as cargas em movimento curvilíneo; contudo sem alterar o módulo de suas velocidades.
Energias em circuitos de corrente

Ao se estabelecer uma corrente elétrica em um circuito real diversas transformações de energia ocorrem simultaneamente ao longo do processo que leva ao crescimento e por fim à manutenção da corrente I em questão. A compreensão destes processos é de grande importância para no estudo e na compreensão dos princípios de funcionamento de qualquer dispositivo elétrico ou eletrônico presente no nosso dia a dia.
Estabelecer uma corrente elétrica requer energia, e a quantidade total de energia requerida é determinável pela soma de várias parcelas: a energia dissipada via efeito joule; a energia que será irradiada na forma de ondas eletromagnéticas; a parcela de energia associada à força contra-eletromotriz encontrada em dispositivos como motores elétricos, esta diretamente convertida em energia mecânica nestes dispositivos; a parcela de energia atrelada ao campo eletrostático estabelecido em virtude do acúmulo de cargas ao longo do circuito, a exemplo a energia armazenada em capacitores elétricos conectados ao mesmo; e a energia que encontrar-se-á diretamente associada ao campo magnetostático atrelado à corrente estabelecida, sendo a última parcela geralmente conhecida por energia magnética.
O efeito joule implica basicamente a contínua conversão de energia elétrica em energia térmica em um material resistivo quando percorrido por uma corrente elétrica. É o efeito associado ao aquecimento das resistências elétricas encontradas nos chuveiros, ferros de passar roupas, aquecedores elétricos, e outros aparelhos cuja principal função seja a de aquecer o ambiente que os cerca. Visto que esta energia elétrica, uma vez convertida em térmica, não é mais passível de ser recuperada em sua forma original - dadas as propriedades da resistência elétrica e do efeito joule - é a esta parcela que associa-se a necessidade de manter-se uma fonte de energia elétrica continuamente conectada aos circuitos elétricos cotidianos a fim de manter-se constante a corrente elétrica através deles. Removendo-se a fonte de energia (fonte de tensão), a corrente rapidamente reduz-se a zero devido às perdas de energia por efeito joule. Em supercondutores - materiais cuja resistência é absolutamente zero - visto que não há a dissipação de energia por efeito joule, uma corrente elétrica constante pode ser mantida por tempo indeterminado sem que se tenha a necessidade de uma fonte de energia elétrica conectada ao circuito. Maiores detalhes sobre resistividade elétrica, supercondutores e efeito joule podem ser obtidas em artigos específicos ligados ao estudo dos circuitos elétricos resistivos e ao estudo da resistividade dos materiais.

Uma parcela de energia também irrecuperável no próprio circuito uma vez a ele fornecida associa-se à parcela de energia radiada na forma de ondas eletromagnéticas, emitidas quando faz-se a corrente elétrica variar de intensidade. Correntes constantes não irradiam ondas eletromagnéticas, contudo ao variar-se a corrente elétrica em um circuito há a emissão dessas ondas, e por conseguinte há radiação de energia e por tal a transferência dessa energia para as vizinhanças do sistema. A quantidade de energia radiada é fortemente dependente da geometria do circuito, e baseado nestes princípios tem-se o funcionamento das antenas rádio-transmissoras: correntes elétricas variáveis no tempo são estabelecidas nos elementos dessas antenas - elementos estes geometricamente dispostos a fim de maximizar a radiação; nelas, devido à permanente variação da corrente - mantida via geradores de correntes alternadas - tem-se a contínua emissão de ondas eletromagnéticas. Maiores detalhes podem ser obtidos em artigos específicos destinados ao estudo das telecomunicações, das antenas, do eletromagnetismo e das ondas eletromagnéticas.
A parcela de energia de interesse no escopo deste artigo corresponde à energia diretamente armazenada na corrente elétrica ou campo magnético associado uma vez que estes tenha se estabelecido no circuito. Aparte a questão de que pode-se com igual valor afirmar ou que a energia encontra-se armazenada no campo magnético ou que esta encontra-se armazenada na distribuição de corrente estabelecidos, fato é que tal energia é passível de ser completamente devolvida ao próprio circuito ao reduzirem-se a corrente elétrica e também o campo magnetostático a ela associado. Entre as duas, a ideia de associar-se a energia ao campo magnético é certamente é muito frutífera no contexto, e geralmente a mais explorada. Tem-se pois a energia magnética.
A energia transferida em virtude da tensão contra-eletromotriz desenvolvida em dispositivos como os indutores elétricos em muito guarda relação com a energia magnética, principalmente no que refere-se ao princípios envolvidos nesta transferência.
A parcela de energia associada ao acúmulo de cargas nada mais é que a energia potencial elétrica associada à distribuição de cargas elétricas no circuito, ou caso seja de preferência, associada ao campo eletrostático determinado por esta distribuição de cargas.
A energia magnética e a corrente
Dada uma determinada geometria - o que implica uma determinada indutância L - para o circuito em consideração, e também uma corrente I de valor pré-definido a percorrer este circuito, verifica-se que a quantidade de energia magnética associada a essa corrente e ao campo magnético estabelecidos é independente de como a corrente atingiu o valor especificado. Pode mostrar-se que nas condições citadas a energia magnética pode ser determinada através da expressão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{mag}= \frac {1}{2} L I^2 }


A dedução dessa expressão passa por uma importante consideração: a de que a força magnética não realiza trabalho, e por tal não pode ser a responsável pelo processo de transformação de energia que culmina com energia armazenada na forma de energia magnética no circuito em questão. Em verdade a força associada a essa transferência de energia é uma força elétrica, esta correspondendo à força diretamente atrelada à tensão induzida Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } que surge no circuito devido à sua autoindução e à variação do fluxo magnético nesse provocada pela necessária variação de corrente durante o processo que estabelece o valor estático I da corrente nesse circuito.
A tensão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } é determinável a partir da Lei da Indução de Faraday antes comentada. Associado o fato de que o fluxo magnético através de um circuito devido à sua autoindução pode ser determinado pelo produto entre a indutância deste circuito e a corrente que o percorre, tem-se que:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \frac {d \phi}{dt} = L\frac {dI}{dt} }
Como a potência desenvolvida em um certo tempo t é dada pelo produto entre a tensão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } e a corrente I no tempo t em consideração, tem-se que a taxa de conversão de energia elétrica em magnética (a potência) no tempo t em questão pode ser determinada por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {dE_{mag}}{dt} = L{I_{(t)}}\frac {dI_{(t)}}{dt} }
A integração da expressão acima do instante em que a corrente era zero até o instante em que esta atinge o valor I especificado leva diretamente à expressão inicialmente citada para a energia magnética armazenada em um circuito com indutância L percorrido por uma corrente I.
A densidades de energia e o campo magnéticos
Aplicando-se um pouco de álgebra vetorial à expressão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{mag}= \frac {1}{2} L I^2 } é possível expressá-la em termos do campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } estabelecido pela corrente I, do vetor potencial magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } estabelecido pela mesma corrente, ou mesmo, para fins de simplificação, em função dos dois - visto que ambos encontram-se intimamente relacionados via expressão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \nabla \times \vec A } . Procedendo-se os cálculos pode-se demonstrar que a energia magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{mag} } também é determinável via expressão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{mag} = \frac {1}{2\mu_0} \int_{vol.} B^2 dv - \frac {1}{2\mu_0} \int_{sup.} (\vec A \times \vec B) \vec {da} }
A primeira parcela da expressão acima corresponde a uma integral de volume do quadrado do valor de B ao longo de todo um volume escolhido de forma a no mínimo encerrar toda a distribuição de corrente I do circuito, e a segunda parcela corresponde a uma integral de superfície do produto vetorial entre o vetor potencial magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } e o campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } ao longo de toda a superfície fechada que define o volume v em consideração na primeira parcela. Como a única restrição associada ao volume é a de que este encerre todo o circuito em consideração, este volume pode ser feito tanto maior quanto se queira. Verifica-se que à medida que o volume em consideração é tomado cada vez maior, a integral de volume resulta um valor certamente maior e a de superfície um valor cada vez menor, isto de forma que a soma de ambos resulte sempre um mesmo valor, o valor da energia magnética associada ao circuito. No limite em que o volume estende-se até o infinito a integral de superfície anula-se, e em tal situação tem-se:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{mag} = \frac {1}{2\mu_0} \int_{vol.} B^2 dv }
a ser calculada sobre todo o espaço (sobre o universo).
A título de curiosidade, esta expressão é, feita as devidas associações, análoga à expressão que permite o cálculo da energia armazenada em um campo eletrostático:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{eletr.} = \frac {\epsilon_0}{2} \int_{vol.} E^2 dv }
onde E aqui representa o valor do campo elétrico e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_0 } representa a permissividade elétrica do vácuo.
Ao contrário do que parece, as expressões anteriores encontram diversas aplicações práticas, e através delas pode-se concluir, mediante a ideia de que a energia encontra-se armazenada no campo - tanto magnético como elétrico - que a densidade volumétrica de energia magnética associada a um ponto onde o campo magnético possui valor B é dada por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{E.mag} = \frac {1}{2\mu_0} B^2 }
e que a densidade de energia elétrica associada a um ponto onde o campo elétrico possui valor E é dado por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{E.eletric.} = \frac {\epsilon_0}{2} E^2 }
Se a preferência for pela ideia de que a energia magnética encontre-se armazenada na distribuição de corrente e não no campo magnético em si, é possível expressar a integral anteriormente citada como:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{mag} = \frac {1}{2} \int_{vol.} (\vec A . \vec J) dv }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec J } representa a densidade de corrente e a integral de volume é tomada novamente sobre todo o espaço.
Neste caso diz-se que a energia está armazenada na distribuição de corrente, em densidade volumétrica igual a:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{E.mag} = \frac {1}{2} (\vec A. \vec J) } .
O magnetismo e a matéria

É sabido que as partículas atômicas fundamentais - elétrons, prótons e nêutrons - possuem momentos angulares intrínsecos, e que os prótons e elétrons, em virtude de serem partículas carregadas, também possuem momentos magnéticos intrínsecos. Também é sabido que os elétrons encontram-se dotados de energia cinética, e por tal em movimento, ao redor dos respectivos núcleos em uma estrutura atômica neutra, e que as partículas que compõem o núcleo também não encontram-se estáticas na estrutura que juntas formam.[23]
É certamente de se esperar, pois, que a interação magnética seja pertinente à compreensão da estrutura atômica e da matéria conforme concebida hoje, e que toda e qualquer matéria, de forma sensível aos sentidos humanos ou não, responda, de alguma forma e com alguma intensidade, ao menos microscopicamente, às influências externas de origem magnética (a campos magnéticos). É sabido que uma das parcelas da interação magnética total que a matéria exibe frente à influências magnéticas externas - interação total esta certamente dependente das particularidades de cada material - é traduzida por uma tênue repulsão magnética entre o objeto e as fontes magnéticas externas, e que esta parcela, mesmo que em um significativo número de casos mostre-se mascarada por parcelas atrativas ou repulsivas muito mais intensas, encontra-se sempre presente. Materiais que possuem estruturas que não impliquem outras parcelas além desta pequena repulsão são enquadrados em uma classe de materiais designada por materiais diamagnéticos. O diamagnetismo, embora não implique que todos os materiais sejam diamagnéticos, é pois inerente à estrutura de toda a matéria.
É importante de antemão ressaltar ao se estudar a relação entre magnetismo e matéria que os campos em consideração são, assim como para o caso elétrico, salvo exceções explícitas, os campos macroscópicos, ou seja, os campos termodinamicamente mensuráveis. Os campos macroscópicos correspondem ao valores médios das flutuações inerentes dos vetores campo magnéticos ou elétricos nos pontos em consideração, flutuações estas decorrentes da complexa dinâmica das partículas que compõem a matéria em si. Cita-se que os campos magnético e elétrico nas proximidades de um elétron são certamente muitíssimos maiores do que quando este encontre-se apenas um pouco distante do ponto em consideração. O valor real do campo em um dado ponto da estrutura da matéria pode sofrer variações consideráveis tanto em módulo como em sentido em curtíssimos intervalos de tempo, contudo, os valores médios adequadamente associados representam o estado termodinâmico do sistema e o comportamento macroscopicamente mensurável da matéria, constituindo estes últimos o alvo de estudo em questão. Recursos oriundos do formalismo termodinâmico aplicam-se indubitavelmente com justo valor ao estudo dos sistemas vinculados.
Antes que se siga adiante na busca por uma compreensão mais detalhada acerca dos mecanismos de respostas da matéria frente à influências magnéticas externas deve-se primeiro fazer uma descrição fenomenológica e estabelecer o conceito de magnetização.
Magnetização

O termo magnetização refere-se ao fenômeno de resposta da matéria frente a campos magnéticos excitantes, na maioria dos casos frente a campos excitantes externos. Quando se imerge um pedaço de matéria qualquer em uma região onde há uma campo magnético preexistente, a estrutura deste material responde ao campo no qual fora imerso mediante a produção de um campo magnético próprio, cuja intensidade e orientação dependem não apenas do campo externo excitante como também das propriedades do material que compõe o objeto em questão. Diz-se então que o material encontra-se magnetizado.
A magnetização do material mostra-se, nos casos mais simples - para materiais isotrópicos, homogêneos e não fortemente magnetizáveis - diretamente dependente do campo magnético excitante. Em tais casos a magnetização é nula quando o campo magnético indutor também é nulo, e cresce gradualmente, a favor (paramagnetismo) ou contra (diamagnetismo) - mas contudo paralela - ao campo excitante a medida que a intensidade deste último aumenta. Entretanto, em casos mais específicos - o que depende diretamente da natureza e estrutura do material em questão - a magnetização pode relacionar-se com o campo magnético externo de formas bem mais complicadas, havendo a necessidade do uso de tensores ou ferramentas matemáticas mais avançadas para descrevê-la, e em casos extremos, esta pode inclusive depender do histórico de exposição às influências magnéticas externas[26] - fenômeno notoriamente visível em materiais que exibem memória e histerese magnéticas.
Materiais que possuem histerese magnética podem encontrar-se magnetizados mesmo na ausência de campo excitante em um dado momento, e podem, em virtude de seu histórico, exibir magnetização nula mesmo quando imersos em campos excitantes não nulos.
Os ímãs permanentes são compostos por materiais que apresentam, em seu estado de equilíbrio termodinâmico ou em estados metastáveis com longos tempos de vida - uma magnetização notoriamente não nula. Embora tais materiais certamente respondam a campos excitantes externos de forma que a sua magnetização total mostre-se não obstante também dependente da excitação externa, os imãs permanentes diferem dos demais materiais por associar-se a eles uma parcela de magnetização permanente não nula com origem na própria estrutura do material - com um certo abuso de linguagem, com origem em uma "autoexcitação" magnética - sendo esta parcela em específico para a maioria dos casos completamente independente de uma excitação magnética externa.
A magnetização e a densidade de momento de dipolo magnético

Um exame ao microscópio ou com técnicas mais específicas revela que um material torna-se magnetizado mediante um maior ou menor alinhamento - induzido pelo campo excitante - de um enorme número de minúsculas regiões magnética, por vezes denominadas domínios magnéticos.Predefinição:Nota de rodapé Estas minúsculas regiões funcionam cada qual como um momento de dipolo magnético orientado em uma dada direção. Como a magnetização total do material é o resultado da maior ou menor cooperação de todos estes dipolos, a medida da magnetização deriva diretamente da medida do momento de dipolo efetivo em cada minúscula região - em cada minúsculo dipolo - ou seja, associa-se à densidade volumétrica de momento de dipolo magnético:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M } = média vetorial do momento de dipolo magnético por unidade de volume ao longo de todo o volume considerado.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M = \frac {\Sigma \vec m_{(\vec {r'})}}{V} } ,[1] em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{(\vec {r'})} } representa cada um dos momentos de dipolo magnético presentes no interior do volume V considerado.
O vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M } é denominado magnetização do material.
A unidade de magnetização corresponde pois à unidade de momento de dipolo magnético, no Sistema Internacional de Unidades o ampère metro quadrado (A.m²), dividida pela unidade de volume, o metro cúbico (m³). Tem-se pois que a unidade de magnetização é o ampère por metro (A/m). Quanto maior a magnetização, maior o momento de dipolo magnético efetivo associado a cada minúsculo volume do material, e maior o momento de dipolo magnético total associado ao objeto.
Para um material linear, isotrópico e homogêneo definindo um objeto com simetria axial adequada - a exemplo um cilindro maciço com eixo devidamente orientado de forma paralela ao campo magnético excitante, este em um campo uniforme, condições estas assumidas por simplicidade - a magnetização do material corresponderia ao momento de dipolo induzido associado ao objeto em tais condições dividido pelo seu volume total.
É importante ressaltar que embora a quantificação da magnetização tenha sido apresentada mediante o conceito de domínios magnéticos diretamente observáveis, a identificação visual destes não se faz necessariamente obrigatória, sendo possível reduzir-se a escala do problema até o nível atômico, e se ainda necessário, por extrapolação, além deste limite. Desta forma o conceito de magnetização pode ser aplicado ao estudo dos próprios domínios magnéticos, se requisitado. Não obstante, a magnetização é extrapolada a uma grandeza espacialmente contínua e não espacialmente quantizada; para todos os efeitos o material passa a ser descrito como composto por infinito número de domínios (dipolos) magnéticos efetivos idênticos, cada qual com momento de dipolo e volume com valores diferenciais.[1] Neste caso:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M = \frac {d \vec m}{dv} }
Tal definição aplica-se de forma justa aos materiais homogêneos e isotrópicos.
A magnetização e o campo magnético
O campo magnético devido a um objeto dotado de uma magnetização M conhecida pode ser determinado através do campo magnético produzido por cada um de seus minúsculos dipolos magnéticos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } . Em termos de vetor potencial magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A } tem-se, para um dipolo puntual:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A(\vec r) = \frac {\mu_0}{4 \pi} \frac {\vec m \times \vec (\vec r - \vec {r'})}{(\vec r - \vec {r'})^2} } [22]
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\vec r - \vec r') } representa o vetor que localiza o ponto onde se determina o potencial magnético - ponto este localizado por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r } considerada a origem do sistema de coordenadas adotado - em relação ao dipolo em questão - este localizado em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec {r'} } se a referência for a origem do citado sistema de coordenadas.
No objeto magnetizado, cada elemento de volume Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dv' = d^3r' } tem associado um momento de dipolo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m = \vec M dv' } , de forma que o vetor potencial total resultante devido à magnetização do objeto é:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A(\vec r) = \frac {\mu_0}{4 \pi} \int \frac {\vec M(\vec {r'}) \times \vec (\vec r - \vec {r'})}{(\vec r - \vec {r'})^2} dv' }
A execução deste cálculo depende, entre outros, de se conhecer não somente o volume mas também a geometria objeto, exigindo doravante dados específicos a cada problema.
Sobre as correntes sem alforria
Mediante algumas ferramentas matemáticas é possível reescrever a expressão anterior para o vetor potencial magnético devido a um objeto magnetizado de forma que essa venha a fornecer algumas informações físicas de considerável relevância aos modelamento teórico dos sistemas associados. Após alguns cálculos - passíveis de serem verificados na literatura pertinente[22] - mostra-se que a expressão anterior pode ser reescrita na forma:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec A(\vec r) = \frac {\mu_0}{4 \pi} \int \frac {\vec J_b(\vec {r'})}{(\vec r - \vec {r'})} dv' + \frac {\mu_0}{4 \pi} \oint \frac {\vec K_b(\vec {r'})}{(\vec r - \vec {r'})} da'}
A compreensão desta expressão leva ao fato de que o vetor potencial e por tal o campo magnético devido à magnetização de um objeto é o mesmo que seria produzido por uma densidade volumétrica de corrente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec J_b (\vec {r'}) = \nabla \times M(\vec {r'})} ao longo da parte interna do material adicionado ao campo produzido por uma densidade de corrente superficial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec K_b (\vec {r'}) = M(\vec {r'}) \times \vec {n} } ao longo da superfície do material, onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec n } representando um vetor unitário normal a esta superfície em cada ponto considerado.Predefinição:Nota de rodapé
De fato verifica-se não apenas teórica mas também praticamente o que a análise matemática sugere: se em um dado ponto o rotacional da magnetização difere de vetor nulo, há associado a este ponto uma corrente elétrica - mais especificamente uma densidade volumétrica de corrente elétrica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec J } - não nula, mesmo esta corrente não correspondendo diretamente a uma corrente elétrica tradicional - que implica o traslado de carga ao longo da estrutura e cuja causa associa-se, para o caso de materiais resistivos, a uma fonte de tensão externa como pilhas ou baterias. As causas da corrente no caso em debate, ao contrário, não associam-se a tais tensões e campos elétricos externos e sim ao campo magnético excitante bem como a forma como a matéria respondeu a esta excitação, ou seja, à magnetização do material. Esta corrente difere pois certamente das corrente convencionais - no contexto tradicionalmente identificadas como correntes livres - e é, dado o mecanismo de sua origem, usualmente denominada corrente ligada.
Assim, distinguem-se doravante na análise do magnetismo atrelado à matéria, por tal, dois tipos de corrente elétrica. A corrente livre, tradicional em análise de circuitos e que implica o traslado de portadores de cargas livres ao longo da estrutura do material ou espaço em consideração, e a corrente ligada, corrente esta resultante da adequada justaposição de um número significativos de minúsculos circuitos elétricos associados às estruturas dos pequenos dipolos magnéticos ligados à magnetização do material. Às correntes ligadas não associam-se pois portadores de cargas livres em movimento, e sim à cooperação de inúmeros portadores de carga que, movendo-se presos cada qual ao respectivo momento de dipolo magnético, ou seja, à respectiva estrutura atômico-molecular que integra o material, também movem-se, dada a justaposição dos minúsculos circuitos, de forma a passarem todos juntos por um dado ponto em questão, implicando neste ponto uma corrente elétrica efetiva de valor consideravelmente maior do que a verificada em cada pequeno circuito de forma independente. O índice "b" é geralmente utilizado para identificar as correntes ligadas, e deriva da expressão inglesa para corrente ligada: "bound current".
Para análise teórica e prática, a magnetização em um material produz os mesmos efeitos que seriam esperados caso existisse apenas uma distribuição de correntes análoga à distribuição das correntes ligadas adequadamente inferidas da magnetização em questão. Tal afirmação vale tanto para o caso de magnetização com rotacional diferente de zero - o que implica uma densidade volumétrica de corrente ligada diferente de zero no interior do material - bem como para magnetização não rotacional - que embora não implique uma densidade de corrente ligada no interior do material, geralmente implica uma densidade de corrente na superfície do material. Para ser mais exato, o magnetismo oriundo de corpos magnetizados, em vista da ausência empírica de monopolos magnéticos - é não apenas análogo ao que observar-se-ia para uma distribuição de correntes livres análoga à de correntes ligadas como é em verdade efetivamente devido às correntes ligadas, ou seja, as correntes ligadas têm existência real e não apenas teórica no interior e superfície do material em consideração.

Dadas as semelhanças entre dipolos extrínseco e intrínseco, a existência de correntes ligadas na superfície do material devido à magnetização é melhor compreendida uma vez considerado que, associado a um vetor momento de dipolo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } , pode-se sempre pensar a existência de uma corrente i circundando-o de forma que o produto dessa corrente pelo vetor área associado ao circuito por ela definido resulte o momento de dipolo magnético em questão. Seguindo-se o raciocínio anterior, associado ao momento de dipolo total do objeto com magnetização uniforme (irrotacional), pode-se pensar corretamente em uma corrente elétrica fluindo pela superfície do material, sendo essa corrente, certamente, também identificável como uma corrente ligada. A área desse dipolo tamanho família corresponde a área da seção do objeto em questão. É imediato compreender que densidade superficial de corrente ligada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_b } associada tem que mostrar-se perpendicular tanto à magnetização Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M } como ao vetor normal à superfície no ponto em questão - encontrando-se esta necessária orientação em virtude da aplicação da regra da mão direita e em vista do fato desta corrente encontrar-se restrita à superfície do material. É fácil perceber que, dados diversos dipolos iguais e de dimensões reduzidas, todos orientados na mesma direção (ver figura), as correntes associadas a cada um deles somam-se na superfície externa que determinam e cancelam-se no interior dessa, de forma que há, ao fim, apenas uma corrente efetiva (contudo ligada) na superfície da estrutura que encerra tais dipolos.
A analogia em discussão no parágrafo anterior remete diretamente à comparação entre o campo de um solenoide simples - este com núcleo a vácuo (ou por aproximação, de ar) - e por tal com corrente apenas na superfície do cilindro que o define - e o campo produzido por um ímã material permanente cilíndrico com dimensões similares e magnetização constante adequadamente escolhida ao longo de sua estrutura, ou seja, em direção axial. A magnetização do ímã é irrotacional, e a tal associa-se, conforme já discutido e aqui esperado, ausência de correntes ligadas no interior deste. Uma vez estabelecido que o campo magnético análogo ao produzido pelo eletroímã (solenoide) em questão, tanto internamente quanto externamente ao mesmo, é análogo ao produzido pelo ímã, conclui-se que à corrente livre existente no solenoide associa-se no ímã material em barra uma corrente ligada de igual valor em sua superfície.
Ressalva-se mais uma vez que, embora apresentado como uma ferramenta teórica para auxiliar na análise dos sistemas físicos em questão, as correntes ligadas nas estruturas dos materiais magnetizados - a exemplo no ímã anterior - têm fundamento físico e são por tal reais, tão reais quanto as correntes ditas livres, embora certamente não tão acessíveis ou controláveis experimentalmente quanto estas últimas.
O grandioso "B" versus o famigerado campo "H"

Uma vez compreendido que a magnetização implica campo magnético diretamente associado, é hora de colocar na balança não apenas o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_M } devido à magnetização mas também o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_0 } que estaria presente na região na ausência do objeto magnetizado, sendo este devido às fontes magnéticas externas e geralmente - mas não necessariamente - o responsável por induzir a referida magnetização no material. É notório que o campo magnético total Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } mensurado em um dado ponto do sistema composto é resultante não apenas de uma das citadas parcelas em particular, mas sim da superposição dos campos devidos às duas causas.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \vec B_0 + \vec B_M }
O campo excitante - o campo magnético que estaria presente na região na ausência do objeto magnetizado - que não raro é responsável por induzir a magnetização do material e que por vezes é representado por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_0 } [1][6] - é tradicionalmente - aparte uma constante - conhecido como "campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } ".[22][24]
Tratamento macroscópico - no vácuo
Em virtude de razões práticas, o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } reflete - geralmente mas não de forma obrigatória - o campo devido a correntes livres. A associação com as correntes livres dá-se na prática não raro por planejamento e deve-se ao fato destas correntes, bem como a geometria do circuito envolvido, poderem ser facilmente mensuradas e determinadas na prática com a precisão necessária. Controles na fonte de tensão ou corrente, e galvanômetros, são não obstantes propositalmente instalados para permitir o controle das correntes livres, controle que traduz-se - em problemas práticos assim concebidos - em controle direto do campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } , que pode então ser previamente escolhido e feito presente conforme planejado.
As correntes ligadas - estas associadas à resposta da matéria ao campo excitante ou à auto-magnetização (ímãs) - certamente não são facilmente determináveis ou controláveis na prática. Contudo deve-se perceber que não são raros os sistemas onde há correntes ligadas - sistemas envolvendo ímãs e materiais magnetizados, a exemplo - responsáveis pelo campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } a ser considerado em alguma outra parte do sistema. Exemplo típico encontra-se esboçado na figura ao lado: a magnetização de um prego via campo excitante produzido por um ímã permanente. O campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } em consideração ao assumir-se o prego como objeto móvel em estudo certamente não é um campo devido a correntes livres em sentido de associarem-se à presença de fontes de corrente ou tensão típicas, ou seja, a portadores de carga livres e em movimento ordenado, sendo o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } no prego devido em verdade a correntes ligadas à estrutura do ímã. Assim, tanto correntes livres como correntes ligadas podem constituir fontes de campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } , e associá-lo apenas às correntes livres sem os devidos cuidados não raro leva a situações e resultados incorretos.
Por razões teóricas e também por razões práticas, embora o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } em um dado ponto seja em princípio um campo magnético,Predefinição:Nota de rodapé, a unidade na qual usualmente mensura-se o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } não é a unidade de campo magnético - o tesla - e sim a mesma unidade utilizada ao mensurar-se o momento de dipolo magnético - o ampère por metro (A/m). Tal conversão de unidades é feita mediante uma constante de proporcionalidade escolhida apropriadamente, sendo esta a permeabilidade magnética do meio, no caso a do vácuo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0 } , já antes citada no presente artigo. Assim:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H = \frac {\vec B_{excitante}}{\mu_0} }
Nada impede, contudo, que o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } seja medido em tesla se necessário ou conveniente, o que contudo raramente é feito. Nesse caso opta-se por explicitar diretamente do campo excitante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{excitante} } em detrimento ao campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } . Ao explicitar-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{excitante} } não se deve contudo esquecer que o campo excitante citado geralmente não se comporta, em meios materiais, como um campo magnético tradicional e sim um campo magnético auxiliar, apresentando algumas peculiaridades se comparados ao comportamento esperado para um campo magnético tradicional, a exemplo se comparado ao padrão de comportamento sempre observado para o campo magnético total Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } efetivamente mensurável quer em meios materiais quer no vácuo. Tais peculiaridades justificam por si só a preferência explícita pelo campo auxiliar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } em detrimento de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{excitante} } nesse, e por extrapolação, em todos os casos (ver próxima seção).
Tratamento diferencial - em meio material
Considerado o campo magnético resultante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \vec B_{total} } mensurado em um dado ponto no interior de um corpo material e a magnetização Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M } associada ao respectivo ponto, deriva-se para um tratamento puntual a seguinte relação constitutiva para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } :
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H \equiv \frac {\vec B}{\mu_0} - \vec M }
de onde o campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } devido tanto à magnetização como ao campo excitante é então determinável via expressão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \mu_0 \vec M + \mu_0 \vec H }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } constitui-se pois pela parcela do campo magnético total no ponto que não encontra-se associada à magnetização do meio material no próprio ponto em consideração e vizinhança diferencial imediata, ou seja, pela parcela que encontrar-se-ia ali presente na ausência do momento de dipolo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m = \vec M dv } atrelado ao ponto em consideração.
Para uma análise puntual evidencia-se, via Lei de Ampère, que o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } em um dado ponto é associado à densidade de corrente livre encontrada no ponto:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec H = \vec J_{livre} }
visto que o rotacional da magnetização associa-se à densidade de corrente ligada no ponto em questão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec M = \vec J_{ligado}} .

Retomando o raciocínio anteriormente apresentado para o caso macroscópico, tem-se na relação constitutiva para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } em escala microscópica simplesmente a aplicação do mesmo raciocínio, contudo em escala puntual: o diferencial de volume "dv" que encerra o ponto em consideração é tratado como o "objeto" material, e esse é tratado como estando sob influência de um campo excitante devido a correntes externas - associadas a toda e qualquer corrente presente no restante do corpo macroscópico - excetuado o elemento de volume "dv" - ou mesmo na vizinhança externa ao citado corpo. Mesmo correntes identificadas como correntes ligadas em outras partes do corpo macroscópico são assim tratadas como possíveis fontes de campo excitante no ponto em questão na relação constitutiva conforme apresentada.
Dada a definição anterior, a equivalência do campo auxiliar ou excitante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_0 = \mu_0 \vec H } a um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } se dá com precisão na ausência de magnetização (no vácuo), contudo deve ser feita de forma cautelosa no interior da matéria. Interno à estrutura da matéria, o campo magnético (auxiliar) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_0 } não segue todas as características de um campo magnético tradicional (o que por vezes justifica o uso da expressão "campo auxiliar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } " em detrimento de campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B_{excitante}} ). Em particular, enquanto para qualquer campo magnético (total) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } verifica-se sempre a ausência de divergência - o que reflete a ausência empírica de monopolo magnético e implica que as linhas representativas do campo magnético sejam linhas sempre fechadas - para o campo auxiliar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } verifica-se experimentalmente que uma divergência não nula na magnetização do material em um dado ponto atua - de forma parecida ao que esperar-se-ia de uma "carga de campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } " - como fonte de campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } - o que implica que a divergência do campo auxiliar não é obrigatoriamente sempre nula. As linhas do campo auxiliar podem assim, ao contrário das linhas de campo magnéticas, divergirem ou convergirem para pontos materiais específicos. Calculando-se o divergente a partir da relação constitutiva deduz-se, visto que
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \vec B = 0 } (sempre)
o seguinte resultado:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla . \vec H = - \nabla \vec M }
que, conforme verificação empírica, não tem associado a obrigatoriedade de anular-se.
No ponto acima encontra-se a justificativa para não associar-se as fontes de campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } exclusivamente a correntes livres. Embora seja verdade que o rotacional do campo auxiliar deva-se apenas à presença de correntes livres
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \vec H = \vec J_{livre} } ,
fato que considerado isolado induz à associação errônea entre campo auxiliar e as correntes livres - e que leva os mais desatentos a fazer uso tolo da associada e válida lei de ampère em sua forma integral para o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } :
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \oint \vec H.\vec {dl} = I_{livre} }
a ausência de correntes livres não é suficiente para garantir a nulidade do campo excitante.
Tem-se bom exemplo quando considera-se o campo auxiliar devido apenas um ímã cilíndrico em forma de barra portando magnetização constante. Embora haja a ausência completa de correntes livres e, uma vez explorada a simetria do problema, a integral de linha em caminho fechado do campo auxiliar resulte sempre em zero, tais fatos não implicam o campo auxiliar por ele devido como sendo nulo. O campo auxiliar devido ao ímã certamente não é nulo, tão pouco o é o campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \mu_0 \vec H } a ele devido na região que o cerca (suposta em vácuo).
Mídias lineares e não lineares
Ao se estudar o comportamento magnético da matéria a primeira consideração usualmente feita é dividi-la em dois grandes grupos, um encerrando os materiais que não possuem magnetização permanente e que respondem de forma proporcional a campos excitantes moderados, e outro encerrando os materiais que possuem magnetização permanente ou que respondem ao campo excitante de forma diversas excluída a forma proporcional. O primeiro grupo define o grupo das mídias lineares enquanto o segundo define o grupo das mídias não lineares. O estudo normalmente se inicia com enfoque no primeiro grupo visto que a linearidade da resposta permite consideráveis simplificações teóricas e práticas.
Susceptibilidade e permeabilidade magnéticas
Em mídias lineares a magnetização Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M } é, em cada ponto do meio material, diretamente proporcional ao campo excitante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } . A constante de proporcionalidade é conhecida por suscetibilidade magnética e geralmente representada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_m } .
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M = \chi_m \vec H }
A suscetibilidade magnética é uma grandeza adimensional (sem unidades) que varia de substância para substância, apresentando valores positivos para as mídias paramagnéticas e negativo para mídias diamagnéticas. A tabela abaixo apresenta alguns valores para a suscetibilidade magnética de alguns elementos e materiais típicos.
| Diamagnéticos | Paramagnéticos | ||
|---|---|---|---|
| Material | Suscetibilidade | Material | Suscetibilidade |
| Bismuto | -1,6 x 10 -4 | Oxigênio | 1,9 x 10 -6 |
| Ouro | -3,4 x 10 -5 | Sódio | 8,5 x 10 -6 |
| Prata | -2,4 x 10 -5 | Alumínio | 2,1 x 10 -5 |
| Cobre | -9,7 x 10 -6 | Tungstênio | 7,8 x 10 -5 |
| Água | -9,0 x 10 -6 | Platina | 2,8 x 10 -4 |
| Dióxido de Carbono | -1,2 x 10 -8 | Oxigênio líquido (-200 °C) | 3,9 x 10 -3 |
| Hidrogênio | -2,2 x 10 -9 | Gadolínio | 4,8 x 10 -1 |
A suscetibilidade magnética pode depender de forma considerável das condições físicas do material. O gadolínio, a exemplo, é ferromagnético em temperaturas abaixo de sua temperatura de Curie, 15 °C, condição que eleva dramaticamente sua suscetibilidade (caso ainda aplicável).
Relembrando a equação geral para o campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } :
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \mu_0 \vec H + \mu_0 \vec M }
em mídias lineares a situação se escreve:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \mu_0 (\vec H + \vec M) = \mu_0 (1+ \chi_m) \vec H }
ou
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B = \mu H }
onde
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = \mu_0(1+ \chi_m) }
A constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu } é a chamada permeabilidade magnética ou, especificamente, a permeabilidade magnética absoluta do material.
No vácuo não há magnetização e por tal a suscetibilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{m}} do vácuo é nula. Sua permeabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = \mu_0 } , sendo esta a razão da constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0 } ser tradicionalmente nomeada permeabilidade magnética do vácuo. A permeabilidade absoluta do material possui a mesma dimensão da permeabilidade do vácuo, e geralmente suprime a aparição dessa última em expressões associadas a meios materiais lineares.
Caso queira-se deixar em evidência a permeabilidade magnética do vácuo, define-se ainda a permeabilidade magnética relativa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_r } do material - tradicionalmente também nomeada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_m } por alguns autores - como a razão entre as permeabilidade absoluta do material e a permeabilidade do vácuo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_r = k_m = \frac {\mu}{\mu_0} = (1 + \chi_m) }
Ao contrário da permeabilidade absoluta do material, que possui unidade, a permeabilidade relativa do material é, assim como sua suscetibilidade magnética, adimensional, e por tal geralmente figura acompanhando da permeabilidade magnética (absoluta) do vácuo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0 } nas expressões associadas.
Uso típico
Um exemplo típico e interessante implicando o uso de materiais lineares e das constantes que o caracterizam já foi apresentado em seção anterior no corrente artigo. A indutância de um toroide com núcleo a vácuo é determinável conforme visto pela expressão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{Toroide} = (\frac {\mu_0N^2h}{2 \pi} ln \frac {b}{a}) } (núcleo em vácuo)
Repare a presença da permeabilidade do vácuo na expressão. Caso no núcleo tenha-se agora um material com comportamento magnético linear essa indutância mostrar-se-á certamente diferente. Ela será em verdade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_m } vezes maior, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_m } representando a permeabilidade magnética relativa do referido material.
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{Toroide} = k_m (\frac {\mu_0N^2h}{2 \pi} ln \frac {b}{a}) } [1] (núcleo material)
Figuram na expressão acima tanto a permeabilidade relativa do material quanto a permeabilidade absoluta do vácuo. Pode-se contudo ainda escrever:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ind._{Toroide} = (\frac {\mu N^2h}{2 \pi} ln \frac {b}{a}) } (núcleo material)
onde há agora apenas a permeabilidade magnética absoluta Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu } do material. A permeabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0 } do vácuo não encontra-se mais explicitamente presente.
Histerese magnética

O comportamento magnético de materiais classificados no grupo dos materiais não lineares - ou mesmo de materiais classificados no grupo dos materiais lineares quando sob condições que transcendem as de linearidade - é habitualmente descrito através de curvas de resposta magnética que discriminam ou a magnetização do material em função do campo excitante (M x H) ou o valor do campo magnético total observado em função do campo excitante aplicado (gráfico B x H). Esses gráficos são tradicionalmente conhecidos como gráficos de histerese.
A primeira forma de desviar-se do comportamento magnético proporcional descrito na seção anterior encontra-se atrelada ao demasiado aumento da intensidade da excitação magnética Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } aplicada a um material. Verifica-se que mesmos os materiais classificados no grupo dos materiais lineares deixam de responder proporcionalidade ao campo excitante quando o valor desse atinge patamares os mais elevados, ocorrendo então o que se denomina por saturação magnética do material.
A saturação magnética resulta do alinhamento de todos - ou praticamente todos - os momentos de dipolo magnéticos disponíveis no material quando sob campo excitante (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } ) intenso o suficiente, de forma que aumentos subsequentes em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } doravante deixam de ter efeito por não haver mais dipolos a serem alinhados. O material exibe, na saturação, a máxima magnetização possível. A proporcionalidade entre a magnetização induzida Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M } e o campo excitante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } em mídias lineares é valida apenas para valores moderados desse último; em condições onde uma significativa parcela dos momentos de dipolo (ou domínios magnéticos) ainda não mostram-se completamente orientados pelo campo excitante. Em mídias lineares observa-se contudo que, reduzido o campo excitante, restaura-se a proporcionalidade, e removido o campo, não há mais magnetização macroscópica mensurável no material.
Há, contudo, materiais que apresentam memória magnética, dos quais os materiais a base de ferro constituem exemplos típicos. Nesses materiais a magnetização em um dado instante de tempo depende não apenas da excitação presente no exato instante como também de todo os histórico magnético do material. Cita-se para compreensão o comportamento idealizado de uma material com elevada histerese, esse esboçado no gráfico M x H idealizado ao lado: partindo-se de uma barra de material desmagnetizada em ausência de campo excitante (origem no gráfico), sujeitando-a a um campo excitante crescente observa-se resposta inicialmente proporcional ao campo excitante dada a magnetização gradual do material. Elevando-se o campo excitante a patamares maiores, deixa-se a região e proporcionalidade e aumentando-o ainda mais atinge-se a saturação. Reduzindo-se contudo a excitação, observa-se que a magnetização não se reduz de forma compatível com a redução da excitação; a curva desenhada com o decréscimo do campo excitante não se sobrepõe assim à desenhada durante o processo que levou ao valor máximo do campo excitante. Verifica-se que mesmo após completamente removida a excitação ainda há uma magnetização residual apreciável no material, no gráfico muito próxima à magnetização observada na saturação (interseção da curva com o eixo vertical, acima). É necessário a aplicação de um campo excitante em direção inversa (negativo) com apreciável valor para anular-se novamente a magnetização do material (interseção da curva com o eixo horizontal, à esquerda), e um campo de módulo ainda maior para inverter-se à magnetização até a saturação em direção inversa (ponto extremo inferior do gráfico, terceiro quadrante, o mais à esquerda). O processo se repete de forma similar ao anterior à medida que reduz-se o campo excitante a zero (interseção do gráfico com eixo vertical, abaixo) e posteriormente aumenta-se o campo em direção positiva até atingir-se uma magnetização nula (interseção da curva com o eixo horizontal, à direita) e novamente saturação em direção compatível com a primeira saturação (ponto superior no primeiro quadrante, o mais à direita).
A curva de histerese para uma dado material mostra-se usualmente muito dependente não apenas do material mas também das condições física em que esse se encontra (destaque para a temperatura), e também da frequência com que se percorre a curva, ou seja, da frequência do campo excitante. Mostra-se também muito dependente do valor máximo do campo excitante utilizado.
A histerese é fator importante ao selecionarem-se materiais para compor núcleos de transformadores ou bobinas visto que associado à histerese há um custo energético nem sempre desconsiderável; a inversão "forçada" da magnetização do material requer energia. Também é fator importante na escolha de materiais onde far-se-á o registro magnético de dados digitais ou analógicos.
As curvas de histerese magnética podem ser facilmente determinadas para os materiais nos núcleos de transformadores através de um osciloscópio, uma fonte de tensão alternada e alguns componentes auxiliares. Ao lado tem-se um exemplo prático de curvas de histerese mensuradas para uma amostra de aço adequadamente preparada (técnica experimental contudo desconhecida).
Classes magnéticas
A resposta da matéria à presença de um campo magnético excitante ou mesmo o fato desta possuir ou não uma magnetização permanente encontra-se diretamente relacionada às propriedades particulares de cada material a se considerar. Possuindo momentos de dipolo intrínsecos, a forma como as partículas fundamentais integrantes da matéria interagem e se distribuem para formar um átomo, íon ou molécula - sendo de particular relevância os elétrons, seus orbitais e a distribuição eletrônica nas estruturas que formam - bem como a maior ou menor interação entre átomos, íons e/ou moléculas vizinhas fazem com que materiais diferentes possam apresentar comportamentos magnéticos macroscópicos e respostas a um campo magnético externo também bem diferentes. No estudo do magnetismo convencionou-se dividir os diversos materiais em classes magnéticas a fim de sistematizar a compreensão dos diversos comportamentos magnéticos observados. As estruturas materiais são pois classificadas em cinco classes magnéticas, cada qual caracterizada por um certo conjunto de propriedades particulares. São elas: a classe dos materiais diamagnéticos, dos paramagnéticos, dos ferromagnéticos, dos antiferromagnéticos e por fim a classe dos materiais ferrimagnéticos.
Não encontra-se no escopo da discussão que se segue os pormenores acerca dos modelos teóricos que elucidam as características de interação pertinentes a cada grupo, sendo doravante fornecida apenas os argumentos teóricos fundamentais. Dada a extensão, detalhes teóricos acerca de cada classe implicam por si só à edição de artigo específico para cada classe ("Ver artigo principal").
Diamagnetismo

Embora, conforme antes referido, o diamagnetismo seja uma propriedade em princípio inerente a toda e qualquer matéria, caracterizando-se por uma fraca repulsão magnética entre a matéria e campos magnéticos de natureza externa, encontram-se nesta classe magnética apenas os materiais que não exibem nenhuma outra forma de interação magnética a não ser a antes citada e doravante elucidada. Nestes termos materiais classificados como diamagnéticos são assim fracamente repelidos por fontes magnéticas externas, e não apresentam magnetização quando em ausência de campo excitante (campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec H } ). Materiais diamagnéticos típicos são caracterizados por uma susceptibilidade magnética negativa da ordem de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-6} } , podendo entretanto ter valor -1 no caso dos diamagnéticos perfeitos - os supercondutores.
Materiais diamagnéticos não possuem momentos de dipolo permanentes. Possuem estruturas que lhes conferem magnetização nulas na ausência de campos excitantes de forma que a resposta à aplicação desses será devida aos momentos de dipolos induzidos no ato da excitação.
A origem do diamagnetismo encontra-se na Lei de Lenz e na distribuição eletrônica dos átomos. A Lei de Lenz estabelece basicamente que a variação do fluxo magnético em um circuito fechado de corrente faz surgir nesse uma força eletromotriz induzida - e por tal uma corrente elétrica induzida - sempre em sentido o necessário para que o campo magnético criado pela corrente induzida oponha-se à variação do fluxo que a induz. Olhando-se a estrutura atômica de cada átomo sob ponto de vista adequado à situação vê-se vários circuitos elétricos fechados envolvem o núcleo, cada qual representado por uma órbita no modelo atômico de Rutherford-Bohr - por um orbital no modelo atômico atual - adequadamente preenchidos com um ou dois elétrons cada (Princípio da exclusão de Pauli).
A submissão de tais circuitos de corrente a um campo magnético excitante faz surgir uma corrente induzida (altera os níveis de energia dos orbitais) de forma que um dipolo magnético induzido tenha orientação contrária ao campo indutor, orientação que leva a uma repulsão entre entre o dipolo induzido e o campo excitante, ou melhor, entre o circuito de corrente e a(s) fonte(s) do campo indutor. Multiplicando-se esse efeito a todos os orbitais e a todos os átomos da estrutura de um material diamagnético tem-se o fundamento da repulsão entre o material e a(s) fonte(s) do campo excitante.
Arquivo:Meissner effect p1390050.ogg A situação pode ser parcialmente exemplificada dependurando-se um leve anel de alumínio com um barbante de forma a compor um pêndulo. Aproximando-se rapidamente um ímã do anel, esse será repelido pelo ímã, o que leva ao deslocando o pêndulo em sentido que o afasta do ímã. Há uma substancial diferença contudo no que observa-se a seguir. Nesse caso, uma vez o ímã feito estático próximo ao anel, não observa-se-á repulsão entre o ímã e o anel. Tal observação deve-se à presença de resistência elétrica no circuito formado pelo anel de alumínio, que dissipa energia e leva a corrente elétrica induzida à extinção, resistência não presente nos circuitos de corrente associados à distribuição eletrônica dos átomos. Se o anel fosse composto por material supercondutor a corrente induzida não cessaria, e a repulsão far-se-ia presente mesmo com o ímã em repouso. O afastamento do ímã levaria a uma supressão da repulsão nesse caso, e leva a uma atração entre o ímã e o anel de alumínio no anterior.
A levitação de um supercondutor sobre um ímã fornece certamente um exemplo bem mais próximo do que ocorre em escala atômica no caso de materiais diamagnéticos. Aproximando-se um supercondutor de um ímã, aquele será por esse repelido (e vice-versa), e a repulsão permanece enquanto o estado de supercondutividade for mantido. Se o material transitar para um estado não supercondutor, devido ao aumento da temperatura a exemplo, a repulsão cessa. O Efeito Meissner é assunto recorrente ao se falar de magnetismo e supercondutividade.
Paramagnetismo
O diamagnetismo é observado em materiais que não possuem estruturas que lhes confiram momentos de dipolo atômicos ou moleculares permanentes. São bons exemplos de materiais diamagnéticos os gases nobres e vários metais como o cobre ([ Ar ] 3d10 4s1) que, doando o elétron mais externo à ligação metálica, permanece com cada um dos íons resultantes em uma configuração fechada - camadas 1,2 e 3 completas - que confere momento magnético nulo aos mesmos.
O paramagnetismo é típico em materiais cujas estruturas eletrônicas ou moleculares implicam momentos de dipolo magnéticos permanentes aos seus constituintes mais fundamentais, contudo sua organização estrutural implica independência de cada um desses constituintes em relação aos demais ao se buscar por uma interação magnética de extensa abrangência entre os associados dipolos. Não há interação magnética de longo alcance entre um dipolo e os seus vizinhos. Uma forma bem simples de se pensar a situação é associá-la a um gás ideal de dipolos magnéticos. Em um gás ideal as partículas não interagem umas com as outras; sua energia interna associa-se apenas à energia cinética das partículas que o integram (energia térmica). No caso do gás de dipolos magnéticos isso equivale a dizer que a energia interna do sistema magnético em consideração independe da orientação espontânea dos dipolos encontrados em sua estrutura - ou mostra-se muito pouco dependente delas - a ponto de não implicar a orientação espontânea dos mesmos quando a amostra encontra-se em ausência de campo magnético excitante externo. A agitação térmica cuida então de mantê-los aleatoriamente orientados, de forma que o material, em ausência de campo magnético excitante, exibe uma magnetização total - macroscopicamente mensurável - nula.
Os dipolos permanentes encontrados nos materiais paramagnéticos (e ferromagnéticos) tem origem essencialmente na distribuição eletrônica dos átomos; nos momentos de dipolo intrínsecos de elétrons (número quântico S) e nos momentos magnéticos atrelados aos movimentos orbitais dos elétrons (número quântico L). A fim de determinar-se o momento magnético resultante para o átomo deve-se considerar o acoplamento entre os dois momentos magnéticos anteriores ao longo de todos os orbitais ocupados por elétrons, assunto que por si só resultaria em um artigo (acoplamentos Acoplamento L-S ou Acoplamento J-J). Há casos em que tem-se primeiro que acoplar todos os momentos magnéticos de spin dos elétrons, todos os momentos magnéticos orbitais, e então proceder a soma para determinar-se o momento magnético total do átomo; e há casos em que deve-se determinar primeiro o acoplamento entre os momentos magnéticos de spin e orbital para cada elétron, e depois somarem-se os resultados para todos os elétrons a fim de determinar-se corretamente o momento magnético total do átomo. Os detalhes quanto aos procedimentos não são aqui abordados por extrapolarem o escopo em questão, contudo encontram-se bem descritos na literatura pertinente.
Submetendo-se um material paramagnético a um campo magnético excitante externo os dipolos magnéticos de sua estrutura tendem a alinhar-se com o mesmo. Associado à orientação de cada dipolo imerso no campo magnético excitante há uma energia potencial que pode ser determinada mediante o produto escalar em o momento de dipolo em questão e o campo ao qual encontra-se submetido
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_p = \vec m . \vec B = m.B.cos \theta } .
O ângulo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } corresponde ao ângulo entre os vetores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } , esse último o campo excitante ao qual o dipolo encontra-se submetido.
Poder-se-ia supor que a aplicação de um pequeno campo excitante levaria à rápida ordenação de todos os dipolos presentes na estrutura do material, resultando em uma rápida saturação da magnetização macroscopicamente mensurável no material e em uma resposta instantânea de atração máxima entre o material paramagnético e a fonte do campo excitante. Entretanto, em sólidos paramagnéticos a energia associada ao alinhamento dos dipolos é, para valores típicos de temperatura e campo excitante, da ordem de grandeza da energia térmica kb.T dos átomos do material. Verifica-se que há em decorrência uma literal competição entre o campo magnético tentando alinhar os dipolos e a temperatura tentando desorientá-los, de modo que a magnetização induzida macroscopicamente mensurável mostra-se dependente tanto do campo aplicado como da temperatura. A uma dada temperatura verifica-se usualmente a proporcionalidade da magnetização macroscópica com o campo aplicado, o que leva os materiais paramagnéticos ao grupo dos materiais lineares. Demonstra-se tanto prática como teoricamente que para materiais paramagnéticos tradicionais a dependência da magnetização total com a temperatura faz-se mediante uma relação inversa.
A dependência da magnetização macroscopicamente observada com o campo magnético e a temperatura encontra-se sintetizada na conhecida Lei de Curie:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec M = C \frac {\vec H}{T} }
onde M é a magnetização macroscopicamente mensurável no material paramagnético, e C uma constante adequadamente determinada para cada material ou situação.
Como a magnetização dá-se de forma proporcional ao campo, o dipolo induzido no material alinha-se com esse, e observa-se em decorrência a fraca atração característica do paramagnetismo entre o objeto magnetizado e a fonte de campo excitante.
Verifica-se que materiais paramagnéticos exibem magnetização total nula quando em ausência de campo excitante, conforme esperado. Em ausência de campo excitante a agitação térmica cuida de manter os dipolos microscópicos orientados aleatoriamente.
Ferromagnetismo
Ferromagnetismo é a existência de magnetização espontânea em pequenas regiões do material de forma independente de um campo excitante externo. Aparte os compostos, os únicos elementos ferromagnéticos são o cobalto, o níquel, o gadolínio, o disprósio, e como o nome da classe sugere, o próprio ferro.[23]
Origem


Em uma abordagem muito simplista e pouco rigorosa, o ferromagnetismo é por muitos citado como resultante de um alinhamento dos momentos de dipolo magnéticos atômicos devido a uma simples interação mútua entre eles, em uma forma que levaria o material ferromagnético a exibir uma magnetização uniforme ao longo de toda a sua extensão. Análises mais atentas frente aos fatos conhecidos mostra que esse não é o caso, e a explicação do ferromagnetismo observado em materiais passa por um conjunto de considerações bem mais complexas do que as encontradas nessa conjectura inicial.
A primeira consideração a se fazer é que a energia de interação entre dois momentos de dipolos vizinhos em um material ferromagnético, se tratados como independentes, não explica o ordenamento desses dipolos. A exemplo, o ferro: determinando-se a energia de interação magnética entre dois de seus átomos quando separados por 3 angstroms (o espaçamento interatômico do ferro), possuindo cada um dos átomos dipolos, supostos alinhados nesse caso, um momento magnético igual a 2,2 magnétons de Bohr, chega-se ao valor de 3,1 x 10−24 joules. Essa energia é equiparável a energia térmica k.T de um objeto à temperatura de 0,22 kelvins, o que expressamente sugere que a interação dipolo-dipolo não pode ser a responsável pela ordenação magnética dos dipolos à temperatura ambiente, tipicamente 300 kelvins.[23] À temperatura ambiente espera-se uma energia térmica por átomo com ordem de grandeza de 10−21 joules, pelo menos mil vezes maior que a anterior. A energia térmica evidentemente sobrepuja por completo a energia de interação magnética.
Ademais observa-se que o material ferromagnético não exibe magnetização uniforme ao longo de toda a sua extensão e sim uma grande quantidade de pequenas regiões, cada qual certamente com magnetização uniforme contudo orientadas, delimitadas as condições físicas, de forma mais ou menos aleatória umas em relação às outras: têm-se os domínios magnéticos.
Verifica-se que a magnetização de materiais ferromagnéticos é dependente da temperatura, sendo máxima à temperatura absoluta nula e caindo a zero em uma temperatura conhecida como temperatura de Curie Tc. Para o ferro Tc = 1 043 K = 770 °C. Acima da temperatura de Curie os materiais passam a se comportar como materiais paramagnéticos sujeitos à Lei de Curie adequada à situação, sendo a susceptibilidade magnética então expressa por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi = C / (T - T_c) } , C uma constante.
A construção de um modelo que elucide as origens do comportamento ferromagnético exigem necessariamente consideração oriundas da mecânica quântica, sobretudo de um processo conhecido como interação de troca, que envolve a simetria das funções de onda que descrevem os elétrons em um átomo ou conjunto interagente de átomos e a indistinguibilidade mediante permutação de posições de partículas idênticas. A interação de troca determina entre outros a orientação dos momentos angulares quantizados (spin) dos elétrons em seus orbitais, quer atômicos quer ligantes, sendo os detalhes acerca dessa influência determinantes para que alguns elementos sejam ferromagnéticos ao passo que todos os demais não.
A construção do modelo passa também pelo fato que a magnetização em materiais ferromagnéticos é em essência devida à orientação dos momentos intrínsecos dos elétrons (spins) e não aos momentos de dipolo magnéticos associados aos movimentos dos elétrons em seus orbitais; por considerações acerca das dimensões dos orbitais d nos metais de transição se comparados à separações interatômicas (parâmetros de rede) características de cada elemento, e por considerações sobre a quantidade de elétrons e sobre a distribuição eletrônica desses nos referidos orbitais.
A situação que leva ao ferromagnetismo implica um balanço delicado entre diversos fatores: é necessário que a subcamada d, que comporta quando cheia 10 elétrons, esteja apenas parcialmente cheia (3d6 no caso do ferro), e que o raio da subcamada d seja suficientemente grande para permitir uma certa superposição espacial entre as camadas de átomos vizinhos e assim justificar a existência de uma interação de troca entre eles, mas por outro lado pequena o suficiente para permitir que a largura de banda de valência não seja demasiadamente grande de formar que, em virtude da degenerescência energética e da localização da energia de Fermi, os orbitais com menor energia em função da interação magnética permaneçam completamente ocupados enquanto orbitais que implicariam orientações de spins contrárias ao dos encontrados no primeiro caso mostrem-se pouco ou efetivamente não ocupados; resultando assim um momento de dipolo magnético total não nulo no domínio em consideração. O parâmetro determinante nesse balanço de distâncias é a razão entre a separação dos núcleos atômicos R e o diâmetro "D" da subcamada d. Verifica-se que valores superior a 1,5 para esta razão levam às condições necessárias para o ferromagnetismo. A exemplo, para o manganês a citada razão é 1,47, ao passo que para o ferro é 1,63, para o cobalto 1,82 e para o níquel 1,98.
A ideia anterior é corroborada pelo fato de que o manganês, um elemento não ferromagnético em condições normais, é utilizado na confecção de compostos ferromagnéticos. As estruturas desses compostos são tais que implicam uma separação um pouco maior para os átomos de manganês em interação, levando-os à condição de exibir comportamento ferromagnetismo. As ligas de Heuster constituem típicos exemplos pertinentes ao caso.
Foge ao escopo desse artigo contudo entrar nos pormenores dos modelos que visam elucidar o ferromagnetismo em seus detalhes visto que esses modelos, em seus pormenores, resultam em artigos com razoável extensão e mesmo livros inteiros, fato facilmente verificável mediante pesquisa na literatura pertinente à área. Encontra-se no escopo desse, contudo, considerações acerca dos domínios magnéticos e do comportamento macroscópico de um material ferromagnético.
Domínios e energias

Tipicamente, reduzindo-se gradualmente a temperatura de um material ferromagnético fundido abaixo da sua temperatura de Curie, embora a formação de domínios aleatoriamente orientados possa ser microscopicamente observada, uma magnetização macroscopicamente mensurável é usualmente verificada. Essa só será observada ser for aplicado um campo magnético excitante externo, o que leva diretamente ao comportamento descrito pela curva saindo da origem no diagrama de histerese idealizado apresentado na correspondente seção.
O comportamento global dos materiais ferromagnéticos descritos em suas respectivas curvas de histerese surgem em virtude da necessidade de se minimizar não uma mas ao todo três energias diferentes contudo diretamente relacionadas ao comportamento magnético do material: a energia magnética associada ao campo magnético macroscopicamente mensurável, a energia associada às fronteiras dos domínios magnéticos, sítios de campos magnéticos intensos, altamente localizados e não uniformes; a energia associada à orientação da magnetização em relação aos eixos de simetria do material cristalino. Tipicamente a minimização dessas energias implica a inexistência de um campo externo se o ponto de partida for o inicialmente descrito acima; os domínios formados, embora com magnetizações uniformes dentro de seus domínios, orientam-se aleatoriamente de forma a se cancelarem mutuamente, impedindo qualquer magnetização macroscópica e por tal a existência de um campo magnético total externamente mensurável.
A aplicação de um campo excitante externo muda a situação, contudo. Percebe-se facilmente que domínios cujas orientações mostrem-se alinhadas com o campo são agora energeticamente favorecidos, e em decorrência observa-se a expansão das fronteiras desses domínio em detrimento dos demais. É também observado empiricamente a rotação da direção de magnetização dos demais domínios em sentido de alinharem-se com o campo excitante. A aplicação do campo excitante leva a uma reconfiguração geométrica e energética do sistema de domínios magnéticos, e a minimização da energia após remoção do campo excitante não implica o imediato retorno à condição inicialmente descrita nos materiais ferromagnéticos. O movimento das fronteiras limites entre domínios não é completamente reversível; sendo inclusive influenciados por imperfeições cristalinas tais como impurezas ou tensões. Observa-se pois que o material permanece macroscopicamente magnetizado mesmo após a remoção do campo excitante, dando origem ao que se denomina magnetização permanente do material. Tem-se então um ímã.
A aplicação de um campo externo em sentido contrário remete diretamente ao comportamento descrito pela curva de histerese do material. A reconstrução das inúmeras fronteiras de domínio suprimidas e a reorientação da magnetização desses envolve energia, devendo essa ser suprida pela fonte de campo excitante sendo aplicado.
Embora a aplicação de campo externo seja o caso mais estudo, há outros processos bem diferentes que também levam a alterações na magnetização de um material ferromagnético. Variações bruscas de fatores físicos como a temperatura ou mesmo a pressão podem certamente induzir a reorientação e redimensionamento dos domínios magnéticos e por tal induzir mudanças na magnetização permanente do material: tratamentos térmicos e choques mecânicos geralmente acarretam efeitos notórios sobre a magnetização permanente do material.
Antiferromagnetismo
As origens da interação antiferromagnética encontram-se, assim como no caso ferromagnético, atreladas às interações de troca que ocorrem entre átomos vizinhos. Assim como no ferromagnetismo a interação implica a existência de momentos magnéticos permanentes nos átomos, mas ao contrário do que ocorre no ferromagnetismo, as interações de troca levam nesse caso ao alinhamento dos momentos magnéticos dos átomos em sentidos opostos, em um processo bem similar ao que ocorre com as orientações dos spins de dois elétrons quando ocupam o mesmo orbital atômico. Materiais antiferromagnético apresentam assim momentos magnéticos efetivos extremamente pequenos para não dizer completamente nulos.
Exemplo de material ferromagnético é o dióxido de manganês (MnO2. Em sua estrutura cristalina o íon negativo de oxigênio encontra-se rodeado por dois íons positivos de manganês. Os momentos de dipolo magnéticos dos dois íons de manganês orientam-se nesse caso de forma oposta dado estarem cada qual também orientados de forma antiparalela com um respectivo elétron do íon negativo de oxigênio, elétrons que por sua vez também têm orientações de spins contrárias, encontrando-se o sistema assim formado em sua configuração de mais baixa energia. A presença íons de um único elemento magnético, no caso o manganês, orientados alternadamente em oposição leva ao antiferromagnetismo observado.
Materiais antiferromagnéticos tradicionalmente não respondem de forma significativa à aplicação de campos magnéticos moderados. Podem vir a fazê-lo de forma moderada se imersos em campos magnéticos exorbitantes, contudo. Nesse caso alguns dos momentos de dipolo magnéticos da estrutura alinham-se paralelos ao campo em detrimento do alinhamento antiparalelo com os íons vizinhos.
Materiais antiferromangéticos também têm suas propriedades dependentes da temperatura. Em temperaturas acima de uma temperatura limite conhecida como temperatura de Néel estes tornam-se paramagnéticos. A denominação "temperatura de Néel" expressa o reconhecimento da relevância dos trabalho de Louis Eugène Félix Néel (1904-2000) na área.
Ferrimagnetismo
Nos materiais inclusos na classe ferrimagnéticos observa-se que a ação da interação de troca leva os momentos de dipolos magnéticos a se alinharem em configuração antiparalela, em um processo muito similar ao observado em materiais antiferromagnéticos. Diferentes desses últimos, contudo, nas substâncias ferrimagnéticas estão presentes dois ou mais tipos diferentes de íons, esses com momentos de dipolo diferentes, de forma que a magnetização resultante não é nula. Há assim a formação de domínios similares aos observados no ferromagnetismo.
Os materiais ferrimagnéticos, também chamados de ferrites, exibem comportamento magnético macroscópico intermediário entre os observados em materiais ferromagnéticos e em materiais antiferromagnéticos. A comportamento dos domínios em ferrites são similares aos observados nos materiais ferromagnéticos no que se refere aos aspectos que levam a uma elevada permeabilidade magnética característica desses materiais. O ferrites magnetizam-se com extrema facilidade. Contudo, ao contrário do observado em materiais ferromagnéticos, os ferrites não retêm magnetização quando o campo excitante é removido.
A elevada permeabilidade magnética dos materiais ferrimagnéticos, quando associada à ausência de campo residual e à baixa condutividade elétrica características desses materiais, faz dos ferrites elementos muito úteis para a confecção de componentes eletrônicos de precisão. Os ferrites são usualmente utilizados para a confecção de bobinas, transformadores e demais componentes eletrônicos magnéticos destinados a circuitos nos quais a presença de correntes induzidas parasitas (correntes de Foucault) bem como as perdas de energia associadas nos núcleos formados por esses materiais mostrar-se-iam intoleráveis caso os tradicionais materiais ferromagnéticos fossem empregados em substituição.
Ferrites são tradicionalmente muito empregados em bobinas destinadas a circuitos de radiofrequência elevadas, bobinas de frequência intermediária (FIs), e como núcleo de antenas magnéticas destinadas à detecção de ondas eletromagnéticas de baixa intensidade.
Nos tradicionais rádios transistorizados portáteis da década de 90, enquanto a antena externa, de metal, dedica-se à detecção de sinais eletromagnéticos na faixa de FM, os sinais de na faixa de AM são detectados por uma antena magnética montada sobre núcleo de ferrite, no interior do rádio. A bobina do próprio circuito destinado à sintonia das estações funciona no caso como antena. Sobre esse ferrite montam-se também a bobina do oscilador local e a bobina destinada à coletar a soma dos dois sinais, todas acopladas magneticamente, sendo o sinal soma resultante coletado então enviado às etapas amplificadoras subsequentes e aos filtros de frequências intermediárias (FIs). Tal configuração é a que confere a notória sensibilidade direcionada ao rádio quando sintonizado na faixa de AM: girando-se o rádio (e o ferrite) sobre eixo perpendicular ao do ferrite percebe-se notoriamente as variações na intensidade do sinal recebido através das respectivas variações no volume do sinal sonoro reproduzido. Há uma posição em que se recebe o sinal de forma mais intensa, e há uma posição em que não se capta praticamente sinal algum. Tal fenômeno, característico das antenas magnéticas (antenas de loop), encontra aplicações importantes. A exemplo é empregado no sistema de navegação aérea, onde os aviões voam guiados pelo direção de recepção dos sinais emitidos por um radiofarol específico, direcionando-se em orientação estabelecida pelo goniômetro quando há recepção nula e não máxima - dada a maior precisão alcançável no primeiro caso.
Aplicações
Diante de tantas aplicações do magnetismo em nossa vida moderna, é um tanto surpreendente saber que, quando Hans Christian Ørsted estabeleceu a conexão entre eletricidade e magnetismo, a única aplicação relevante desse último efeito era nas já há muito conhecidas bússolas. Com a descoberta dos efeitos magnéticos da eletricidade a situação começou a mudar rapidamente. Um dos primeiros avanços técnicos implementados foi a invenção e difusão do telégrafo. Um conversor eletromecânico fundado na atração magnética entre um eletroímã e uma alavanca interpotente com material ferromagnético ao centro era usado para perfurar uma fita de papel em uma sequência de pontos e traços que, obedecido um padrão predeterminado pelo código Morse, permitiu pela primeira vez a transmissão de informações a longas distâncias de maneira praticamente instantânea. Fios telegráficos espalharam-se acompanhando as linhas férreas por todos os lados, trazendo a humanidade à era da comunicação elétrica.
Conversores eletromecânicos
Um conversor eletromecânico é um dispositivo capaz de converter energia elétrica em energia mecânica, ou seja, de produzir movimento a partir de correntes elétricas; quase sempre fazendo-o de forma a utilizar diretamente os efeitos associados ao magnetismo. A exemplo os motores certamente são conversores eletromecânicos, encontrando-se o princípio de funcionamento desses já discutido nesse artigo. Há, além dos motores elétricos, outros conversores eletromecânicos mais simples, contudo também muito difundidos. Os tradicionais relés, e os alto-falantes, são exemplos típicos pertinentes ao caso.
Em um relé um eletroímã gera um campo magnético de forma a atrair um elemento móvel - constituído de material ferromagnético - situado em suas proximidades, provocando assim o movimento do sistema mecânico a ele acoplado. Ao cessar a corrente no eletroímã, molas geralmente cuidam de fazer o sistema mecânico retornar a posição inicial de forma que o processo possa se repetir. Nos relés propriamente ditos o circuito mecânico aciona ou desliga um ou mais interruptores elétricos, permitindo assim o controle de correntes elétricas elevadas por uma corrente elétrica de valor bem menor, a corrente da bobina do relé.
Um mecanismo muito similar aos dos relés é encontrado nas trancas automáticas quer de portas residenciais quer em automóveis, encontrando-se a diferença essencialmente no dispositivo conectado ao conversor eletromecânico. No caso da tranca o mecanismo móvel aciona a trava da porta e não o contato elétrico característico do relé. Há casos em que ele aciona os dois, havendo também um interruptor conectado ao mecanismo a fim de indicar a posição atual da trava.
Nos alto-falantes há a inversão de papéis, permanecendo agora o material magnético, no caso um ímã permanente, em repouso, enquanto a bobina é fixada ao dispositivo móvel, no caso um diafragma de papel ou similar. O movimento do diafragma tem por fim comprimir ou rarefazer o ar à sua volta, sendo o alto-falante estruturado de forma a produzir som audível segundo os padrões determinados pela corrente elétrica que se faça circular pela bobina móvel. Em uma explicação simplificada, se a corrente é feita circular em um sentido, o eletroímã formado pela bobina terá polos alinhados com os polos do ímã permanente, o que leva a uma atração entre a bobina e o ímã. A bobina e o diafragma movem-se para dentro, sugando assim o ar à frente do alto-falante. Fazendo-se a corrente circular em sentido contrário os polos do eletroímã se invertem, e se no primeiro caso houve atração, agora verifica-se uma repulsão entre a bobina e o ímã. Tanto a bobina como o diafragma movem-se para fora, pressionando o ar à frente do alto-falante.
A figura ao lado revela a estrutura interna de um alto-falante. Sobressaindo ao centro, similar a uma lata metálica, em papel laminado, o suporte sobre o qual assenta-se a bobina, esta não visível na figura. O ímã, também não visível, com conhecida geometria em forma de anel de espessas paredes, fixa-se sob o chassi metálico. A bobina move-se no interior do orifício no ímã. Há ainda, delimitando a bobina pela parte de dentro, um núcleo de material ferromagnético, esse de tonalidade metálica prateada, bem ao centro na figura. Esse núcleo, também fixo, acopla-se ao ímã de forma a criar um campo magnético sempre perpendicular às espiras na bobina; condição essencial a um melhor desempenho do alto-falante.
Os microfones ditos microfones dinâmicos têm estrutura interna análoga à dos alto-falantes, sendo apenas redimensionadas para uma melhor qualidade na conversão da energia mecânica em elétrica. Trata-se de um conversor "mecanoelétrico", ou seja, um conversor eletromecânico que converte energia mecânica em elétrica. Como recurso emergencial, um alto-falante funciona razoavelmente bem no lugar de um microfone dinâmico. O movimento da bobina induzido pela recepção de sons no diafragma faz variar o fluxo magnético através dessa. Em acordo com a Lei da Indução de Faraday, ter-se-á nos terminais de conexão da bobina uma tensão elétrica diretamente associada ao sinal sonoro sendo recebido. Esse sinal elétrico reproduz o sinal sonoro recebido, e pode ser encaminhado a etapas eletrônicas seguintes, a exemplo, amplificadores e alto-falantes potentes.
Televisores

Os efeitos de campos magnéticos sobre elétrons ou íons quando em movimento no vácuo são amplamente explorados em diversos dispositivos, encontrando-se um deles, ao contrário do que a complexidade associada ao vácuo e à produção de tais partículas carregadas livres possa sugerir, presente no cotidiano de todos. Trata-se da conhecida televisão com tubo de raios catódicos.
Em um tubo de imagem por raios catódicos um canhão de elétrons termoemitidos produz um feixe eletrônico que é acelerado em direção à tela por um campo elétrico intenso estabelecido entre uma tela metálica perfurada (anodo) colocada imediatamente antes da camada fosforescente onde formar-se-á a imagem e o canhão de elétrons no outro extremo do tubo (catodo). A imagem é desenhada um ponto por vez controlando-se a maior ou menor intensidade do feixe incidente. Campos magnéticos gerados em bobinas colocadas em torno do pescoço do tubo cuidam da deflexão tanto vertical quanto horizontal do feixe de elétrons, determinando assim o ponto de incidência do feixe sobre a tela. Há dois circuitos, os circuitos de deflexão vertical e horizontal, que produzem as correntes necessárias nas bobinas de forma a fazer o feixe varrer toda a tela de forma periódica, iniciando no canto superior esquerdo e terminando no canto inferior direito, uma linha por vez. Os campos magnéticos, conforme dito, não são capazes de alterar a velocidade dos elétrons no feixe, mas são capazes de mudar a direção de movimento dos mesmos.
Há no tubo diversos elementos, tanto elétricos como magnéticos, destinados ao foco do feixe sobre a tela fosforescente. Na figura vê-se também uma bobina destinada a esse fim. Essa encontra-se mais presente em televisores coloridos do que em televisores preto e branco dado ser o primeiro em verdade similar a três televisores preto e branco montados em um único tubo. O tubo colorido encerra nesse caso três canhões de elétrons, e uma máscara perfurada (tela matizadora - o anodo) cuida de garantir que cada feixe produzido acerte apenas os pontos fosforescentes correspondentes a uma das cores primárias. A tela é recoberta nesse caso por materiais fosforescentes de três cores diferentes ao invés do tradicional material fosforescente branco presente tubos monocromáticos, sendo dispersos em um padrão simétrico de pontos (ver figura).
As bobinas de deflexão nas televisão com tubo de raios catódicos são montadas sobre uma estrutura de material ferrimagnético. O conjunto é usualmente denominado yoke.
Não é necessário citar que as bobinas encontram-se presentes em praticamente todos os circuitos eletrônicos de uma televisão. Assim como no rádio, há nessa também ao menos um alto-falante.
Armazenamento de dados
Uma das aplicações de materiais com propriedades magnéticas de grande importância na sociedade moderna encontra-se atrela ao armazenamento de dados, quer analógicos quer digitais. Todos que possuem um computador e nele mantêm dados importantes arquivados sabem o quão traumático pode ser a informação de que o disco rígido de sua máquina foi danificado. Em tempos modernos o uso de cartões de crédito também não é estranho a ninguém, e todos estão certamente cônscios da existência de trajas magnéticas no verso desses, tarjas que carregam magneticamente arquivadas as informações importantes a respeito do proprietário, de sua conta e do cartão em si. Até cartões de telefone hoje têm os créditos armazenados em tarjas magnéticas.
Os primeiros dispositivos de armazenamento magnético de informação de amplo acesso foram as fitas, de acesso sequencial, muito populares há décadas atrás como meio para distribuição de músicas, quer na forma de rolos (tapes), quer na forma compacta em caixas de plástico (cassete). Enquanto os tapes destinavam-se ao uso profissional, o cassete caiu rapidamente em domínio público.
As fitas magnéticas eram em essência fitas de plástico flexível e resistente, sempre recobertas com material ferromagnético adequado. Eram posteriormente protegidas com uma camada lubrificante, o que impedia a destruição da mídia magnética quando em atrito com a cabeça de leitura/gravação.
A cabeça de leitura/gravação consistia de uma bobina montada em estrutura adequada capaz de gerar campos magnéticos alternados com amplitude determinada pelo dado a ser gravado, campos que determinavam a magnetização do material ferromagnético impregnado na fita à medida que essa se deslocava sobre a cabeça. A bobina também era capaz de sentir a alternância e a amplitude da magnetização presente na fita à medida que essa se deslocava sobre a cabeça, permitindo assim a recuperação da informação outrora gravada. Em equipamentos de melhor qualidade as cabeças de gravação e leitura eram distintas, e havia uma cabeça exclusivamente destinada a apagar as informações na fita.
Sempre tendo por base o mesmo princípio de funcionamento, a fita cassete foi seguidas pela sua irmã gêmea de maior porte, adequadamente redimensionada ao arquivamento não apenas de áudio mas também de imagens. Inicialmente também disponíveis na forma de rolos (tapes), essas podem ser encontradas às centenas em locadoras de vídeo, ainda na atualidade, em sua forma cassete tradicional. Os tradicionais gravadores videocassetes, embora hoje obsoletos em virtude do advento dos DVDs, são ainda facilmente encontrados ao lado de muitas televisões.
Tradicionalmente armazenam-se dados analógicos em fitas cassete em virtude do acesso sequencial inerente. Os tapes certamente foram empregados, contudo, em sistemas de armazenamento de dados digitais nos primórdios da era digital. Os bancos de dados foram durante longa data guardados em gravadores de rolo que permitiam, embora de forma lenta, o acesso aleatório aos dados arquivados na fita. Marcações de posição eram arquivadas junto aos dados, e os equipamentos tinham a capacidade de posicionar a fita em posição especificada, se de forma rápida para a época, de forma muitíssimo lenta se comparado ao acesso aleatório encontrado em dispositivos modernos, a exemplo nos discos rígidos. Nos primórdios da informática em domínio público havia nos computadores pessoais uma saída destinada à conexão de um gravador cassete comum - dispositivo normalmente utilizado para a reprodução ou gravação de sons - que permitiam o arquivamento de dados digitais quer relativos aos programas quer relativos ao conteúdo gerado pelo usuário nas fitas cassete. O acesso era contudo sistemático, sequencial e lento.

Os tradicionais disquetes utilizados para armazenamento de dados digitais foram desenvolvidos em virtude da ineficiência das fitas proverem acesso aleatório e rápido aos dados digitais. Inicialmente em tamanho família e flexíveis, os disquetes rapidamente evoluíram de forma a terem seu tamanho reduzido e sua capacidade de armazenamento de dados aumentada, sendo as últimas versões distribuídas em caixas de plástico resistentes e não flexíveis. Os primeiros disquetes tinham dimensões da ordem de 8 polegadas e arquivavam meros 80 quilobytes, isso na década de 70. Na década de 90 e na década do milênio seguinte os disquetes eram tradicionalmente encontrados com tamanho de 3 polegadas e meia e capacidade de armazenamento de 1,44 megabytes.
O princípio dos disquetes levou rapidamente aos discos rígidos tradicionalmente encontrados nos computadores modernos. Os últimos avanços na área devem-se à magnetorresistência gigante (GMR), tecnologia que permitiu a popularização de discos capazes de armazenar alguns terabytes de dados. No prólogo do corrente artigo tem-se uma figura ilustrativa e a descrição do princípio de funcionamento de um disco rígido.
Para finalizar, um olhar mais atento elucida que o magnetismo encontra-se presente não apenas na mídia em si responsável pelo arquivamento dos dados como também nos mecanismos necessário ao movimento da cabeça de leitura/gravação e da própria mídia magnética (fita ou disco), em praticamente todos os esquipamentos de armazenamentos de dados tradicionais. É por tal simplesmente essencial à área.
Ressonância magnetonuclear

A técnica de ressonância magnética nuclear, um técnica espectroscópica, fundamenta-se no princípio já descrito de que um dipolo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec m} , quando imerso em um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } , tem uma energia potencial armazenada igual a:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_p = \vec m . \vec B = m.B.cos \theta } .
A técnica fundamenta-se na absorção ressonante de energia eletromagnética - ondas de rádio na faixa de VHF no caso - pelos momento magnético dos núcleos atômicos quando imersos em um intenso campo externo aplicado. Explora-se no técnica a propriedade de quantização da componente z do momento nuclear, no caso o momento magnético, o que em termos leigos significa dizer que o momento nuclear, quando imerso em um campo magnético, pode orientar-se apenas em direções distintas, usualmente duas, "para cima" e "para baixo" (núcleo com spin 1/2). De forma mais clara, a quantização do momento nuclear implica que o ângulo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } na expressão acima é assim restrito a apenas dois valores muito bem definidos, um agudo e um obtuso. Tais valores são contudo diferentes de 0° e 180º, o que leva a precessão do momento angular (e magnético) em torno do eixo Z.
As quantizações do momento angular e de sua projeção no eixo Z definido pelo campo magnético aplicado, amplamente explorados na mecânica quântica, não são exclusividades dos momentos nucleares, e encontram-se presentes em todos os sistemas quânticos, inclusos os momentos angulares de spin e orbitais dos elétrons nas eletrosferas dos átomos.
A quantização do momento magnético nuclear, tradicionalmente sob enfoque na técnica de ressonância o momento nuclear do elemento hidrogênio (do próton), implica que, quando imerso em um campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } predeterminado, esse núcleo orientar-se apenas em duas direções possíveis, ou a favor do campo, ou contra, situações notoriamente distintas pela energia potencial atrelada à orientação do momento em relação ao campo. Há em decorrência uma diferença de energia muito bem estabelecida entre os dois estados de orientação possíveis.
Nas condições descritas acima, ondas eletromagnéticas com a frequência exata, e por tal com a energia de seus fótons no valor exato da diferença de energias entre os dois possíveis estados de orientação nuclear, serão de forma ressonante absorvidas pelos núcleos do elemento, fazendo-os alternar as orientações de seus momentos nucleares em relação ao campo. Uma varredura tridimensional que mensure a quantidade de radiação absorvida ou emitida em cada localidade do espaço permite então determinar as concentrações do citado elemento em diferentes partes do objeto em análise, o que traduz-se na identificação dos diferentes tecidos no interior do corpo de um paciente sobre exame. Os detalhes do processo de tratamento dos sinais são bem mais complicados do que a primeira impressão possa sugerir, mas ao fim tem-se como resultado uma imagem tridimensional do interior do objeto em análise com excelente resolução.
O uso de tal técnica é impossível sem a presença de um intenso campo magnético Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec B } . Na fotografia ao lado tem-se a imagem de um equipamento de ressonância magnética nuclear típico. O enorme cilindro redondo visível na foto encerra um eletroímã de proporções compatíveis responsável por produzir o intenso e uniforme campo magnético necessário à análise em seu interior. O cilindro também encerra os emissores e sensores das ondas de rádio na faixa de VHF necessárias à produção da imagem. O paciente é inserido no núcleo desse eletroímã. No início dessa seção tem-se uma imagem obtida através da técnica.
Ciclotrons e espectrômetros de massa

A capacidade que o magnetismo possui de colocar um feixe de partículas carregadas que se move no vácuo em movimento curvilíneo foi amplamente explorada desde os primórdios da compreensão sobre o assunto, sendo particularmente úteis não apenas em televisões como também em equipamentos mais sofisticados como os cíclotrons, do qual o LHC - Large Hardron Colider - na fronteira entre a França e a Suíça é certamente o maior exemplo, e os espectrômetros de massa, aparelho utilizado entre outros na determinação da massa atômica que figura em praticamente todas as tabelas periódicas de razoável precisão.
A ideia central em ambos os aparelhos é fazer com que a força magnética que atua sobre as partículas do feixe exerça o papel de força centrípeta, levando as partículas a um movimento circular. A força centrípeta Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F_c } em uma partícula de massa m que se move com uma velocidade de módulo v descrevendo uma trajetória circular de raio r é muito bem estabelecida pela física clássica. Igualando-se a expressão citada à conhecida expressão para a força magnética sobre uma partícula de carga q que se mova à velocidade v em um campo magnético B tem-se:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_c = \frac {mv^2}{r} = F_M = qvB sen \theta}
Levando-se em conta que o campo é feito perpendicular ao plano da trajetória circular nesse caso o valor do seno do ângulo que este forma com a velocidade é a unidade. Reescrevendo a expressão acima a fim de determinar-se o raio da trajetória tem-se que:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = \frac {mv}{qB} }

As aplicações são imediatas. Em um espectrômetro de massa prepara-se inicialmente um gás de íons do material a ser analisado utilizando-se para isso variadas técnicas, a exemplo bombardeio por feixe de elétrons, termoemissão, bombardeio por laser e outras. O feixe de íons é colocado em movimento com uma velocidade v, a exemplo por um campo elétrico, e é então direcionado ao interior de um campo magnético uniforme perpendicular à sua velocidade. As partículas iônicas, sobre a ação da força magnética, passam a descrever trajetórias curvas circulares. Conduto, por serem diferentes, quer por constituição elementar quer por constituição isotópica, os diferentes íons têm diferentes massas. Voltando-se a atenção para a equação que define o raio da trajetória a ser descrita por elas vê-se que, dadas a mesma carga (mono-ionização), o mesmo campo magnético e a mesma velocidade, partículas com massas maiores descreverão trajetórias com raios maiores, e partículas com massas menores descreverão trajetórias com raios menores. Ao final de um semicírculo o feixe inicial estará dividido em vários, cada um contendo partículas com determinada massa descrevendo trajetória com um determinado raio distinto dos demais. As diferenças nos raios podem é então utilizadas para comparar as massas das diferentes partículas.
Espectrômetros de massa de grandes proporções, chamados calutrons, que consumiam quando em operação energia elétrica equivalente ao consumo de uma cidade de médio porte, foram utilizados no Projeto Manhattan a fim de promover a separação entre os isótopos altamente físsil (U235) e menos físsil (U238) do urânio durante a segunda guerra mundial. O projeto Manhattan levou à produção da primeira bomba nuclear da história da humanidade. Considerável parte do urânio físsil presente na bomba que destruiu Hiroshima foi separado nesses espectrômetros de massa.

Os cíclotrons são aparelhos construídos a fim de se produzir um feixe de partículas carregadas com elevada energia cinética para o uso em experimentos na área da física de partículas, essa também conhecida como física de altas energias. Aceleradores de partículas lineares foram concebidos e montados, contudo suas enormes dimensões e custos podem podem ser substancialmente reduzidos sem perda de rendimento utilizando-se para tal campos magnéticos que coloquem as partículas em um movimento circular ao invés do movimento linear inicial. Um campo magnético intenso faz o feixe entrar em movimento circular no interior de uma câmara cilíndrica circular, essa dividida em duas câmaras semicirculares com um espaçamento adequado entre elas; em configuração que faz lembrar uma letra D justaposta ao seu reflexo quando vistos por cima. A cada uma das semi-câmaras atrela-se um eletrodo de uma fonte de tensão alternada com frequência adequadamente sincronizada com o movimento do feixe no interior das semi-câmaras. O feixe, injetado próximo ao centro com baixa energia cinética, percorre, dada a baixa velocidade, uma trajetória semicircular de raio pequeno no interior da primeira semi-câmara, e ao entrar no espaçamento entre as semi-câmaras, é acelerado pelo campo elétrico existente entre elas. O feixe entra na segunda semi-câmara com velocidade maior, descrevendo agora trajetória com raio maior. O processo se repete no espaço entre as duas semi-câmaras e o feixe retorna à primeira delas, agora com velocidade maior ainda. O processo é repetido até que o feixe, com elevada energia cinética (velocidade) e já descrevendo a trajetória de maior raio possível no interior do cíclotron, é direcionado para fora do ciclotron, geralmente em direção a um alvo e aos sensores que permitirão a análise dos resultados.
Os cíclotrons descritos foram os primeiros produzidos. Evoluções do mesmo levaram aos sincrocíclotrons e posteriormente aos chamados síncrotrons. Nesse último, um campo magnético variável garante que as partículas movam-se em trajetórias sempre com o mesmo raio mesmo diante do considerável aumento de velocidade experimentado. Os campos magnéticos variáveis são também utilizados para produzir o campo elétrico que acelera as partículas segundo o princípio estabelecido pela Lei da Indução de Faraday.
Comentários finais
Não se pode deixar de citar, ao fim de uma explanação sobre magnetismo, um de seus mais difundidos usos: os adesivos de geladeira. Trata-se de uma aplicação muito prática e comum de "armazenamento de dados" úteis, por muitos também utilizada como forma de arte.
Também é importante comentar que em locais sinalizados com o símbolo internacional de magnetismo (figura ao lado) não se deve entrar com cartões de crédito, chaves, celulares, discos rígidos portáteis, ou qualquer outro objeto metálico ou magnético, que funcione ou seja sensível ao magnetismo. Caso o faça, você poderá ter surpresas muito desagradáveis ou mesmo perigosas à sua integridade física. A propósito, não faça exames de ressonância magnética caso possua peças metálicas implantadas em seu corpo.
Ver também
Referências
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 Halliday, David; Resnick, Robert; Krane, Kenneth S. - Física 3 - 4ª edição - Livros Técnicos e Científicos Editora S/A (LTC) - Rio de Janeiro - 1996
- ↑ 2,0 2,1 Luz, Antônio Máximo Ribeiro da; Álvares, Beatriz Alvarenga - FÍSICA Ensino Médio, Volume 3 - Editora Scipione Ltda. - 1ª Edição - 2007 - ISBN 978-85-262-6510-3
- ↑ http://www.sbf1.sbfisica.org.br/eventos/epef/x/sys/resumos/t0155-1.pdf , conforme acessado em 24-04-11 às 11:40 horas.
- ↑ Gonçalves Filho, Aurélio; Toscano, Carlos - Física para o Ensino Médio - Editora Scipione - São Paulo - 2002 - ISBN 85-262-3977-5 = AL
- ↑ 5,0 5,1 Luz, Antônio Máximo Ribeiro da; Álvares, Beatriz Alvarenga - FÍSICA Volume Único - Editora Scipione Ltda. - 1ª Edição - 2000 - ISBN 85-262-3018-2
- ↑ 6,0 6,1 6,2 6,3 6,4 6,5 6,6 6,7 Gaspar, Alberto - Física , Eletromagnetismo, Física Moderna - Editora Ática - 1ª edição - São Paulo - SP - ISBN 85.08.07529.4
- ↑ 7,0 7,1 Gerard Cheshire (1 de agosto de 2010). Electricity and Magnetism. [S.l.]: Evans Brothers. 26 páginas. ISBN 978-0-237-54185-9. Consultado em 29 de setembro de 2012
- ↑ 8,0 8,1 Penteado, Paulo Cesar M. ; Torres, Carlos Magno A. - Física, Ciência e Tecnologia - Vol. 3 - São Paulo, Editora Moderna - 2005.
- ↑ Yinke Deng (3 de março de 2011). Ancient Chinese Inventions. [S.l.]: Cambridge University Press. 15 páginas. ISBN 978-0-521-18692-6. Consultado em 29 de setembro de 2012
- ↑ P. Zilsel (31 de julho de 2003). The Social Origins of Modern Science. [S.l.]: Springer. 79 páginas. ISBN 978-1-4020-1359-1. Consultado em 29 de setembro de 2012
- ↑ Singhal. Elements Of Space Physics. [S.l.]: PHI Learning Pvt. Ltd. 33 páginas. ISBN 978-81-203-3710-7. Consultado em 29 de setembro de 2012
- ↑ Paraná, Djalma Nunes da Silva - Física Volume Único ; Série Novo Ensino Médio - Editora Ática - 6 Edição - São Paulo 2006 - ISBN 85-08-08628-8
- ↑ Douglas S. Robertson (27 de março de 2003). Phase Change: The Computer Revolution in Science and Mathematics. [S.l.]: Oxford University Press. pp. 57–. ISBN 978-0-19-515748-2. Consultado em 29 de setembro de 2012
- ↑ Joseph F. Keithley (1 de janeiro de 1999). The Story of Electrical and Magnetic Measurements: From 500 BC to the 1940s. [S.l.]: John Wiley and Sons. 61 páginas. ISBN 978-0-7803-1193-0. Consultado em 29 de setembro de 2012
- ↑ Allan H. Robbins, Wilhelm C. Miller (2 de março de 2012). Circuit Analysis: Theory and Practice. [S.l.]: Cengage Learning. 436 páginas. ISBN 978-1-133-28100-9. Consultado em 29 de setembro de 2012
- ↑ Patrick C. Gibbons Ph.D. (10 de novembro de 1992). Physics. [S.l.]: Barron's Educational Series. 119 páginas. ISBN 978-0-8120-4921-3. Consultado em 29 de setembro de 2012
- ↑ P. M. Harman (22 de fevereiro de 2001). The Natural Philosophy of James Clerk Maxwell. [S.l.]: Cambridge University Press. 108 páginas. ISBN 978-0-521-00585-2. Consultado em 29 de setembro de 2012
- ↑ Suresh Garg, Sanjay Gupta, C. K. Ghosh. Wave Optics. [S.l.]: PHI Learning Pvt. Ltd. pp. 8–. ISBN 978-81-203-4500-3. Consultado em 29 de setembro de 2012
- ↑ Telford, William Murray; Telford, W. M.; Geldart, L. P.; Sheriff, Robert E.; Sheriff, R. E. (26 de outubro de 1990). «Applied Geophysics». Cambridge University Press – via Google Books
- ↑ Artigo intitulado "Campo magnético terrestre", conforme publicado na wikipedia lusófona às 13h38min de 4 de abril de 2011 e acessado em 26-04-11 às 17H44min.
- ↑ A rigor tem-se que cargas elétricas movendo-se fora das curvas geodésicas pertinentes irradiam ondas eletromagnéticas. Cargas que movem-se segundo as geodésicas pertinentes não irradiam. Nestes termos tem-se que uma carga em queda livre, embora acelerada para um referencial fixo ao solo, não irradia ondas eletromagnéticas; caso contrário o princípio da equivalência, cerne da relatividade geral, não seria válido. O mesmo se passa para uma carga elétrica em um satélite em órbita de um planeta ou mesmo para o elétron em uma órbita de um átomo conforme inicialmente proposto por Niels Bohr. Em ambos os casos, embora acelerada quando observada de referenciais típicos, a carga não irradia. Um problema acerca desse assunto encontra-se publicado na página "Seara da Ciência" mantida pelo Instituto de Física da Universidade Federal do Seará em sua seção "Eis a questão", subseções "física", "outros assuntos". Procure pela questão 5. Sítio eletrôncio: http://www.seara.ufc.br/questoes/fisica/qoutros.htm
- ↑ 22,00 22,01 22,02 22,03 22,04 22,05 22,06 22,07 22,08 22,09 22,10 22,11 22,12 22,13 22,14 22,15 22,16 22,17 22,18 22,19 22,20 22,21 22,22 22,23 22,24 22,25 22,26 22,27 22,28 22,29 22,30 22,31 22,32 22,33 22,34 22,35 22,36 22,37 Griffiths, David J. - Introduction to Electrodynamics - Third Edition - Editora: Prentice Hall - Upper Saddle River - New Jersey - 1999 - ISBN 0-13-805326-X
- ↑ 23,0 23,1 23,2 23,3 Física Quântica, Átomos, Moléculas, Sólidos, Núcleos e Partículas - Eisberg, Robert; Resnick, Robert - 13ª edição - Editora Campus - 1979 - ISBN 85-7001-309-4
- ↑ 24,0 24,1 24,2 24,3 24,4 24,5 Jackson, John David - Classical Electrodynamics - Third Edition - John Wiley & Sons, Inc - Berkeley - California - 1999 - ISBN 0-0471-30932-X
- ↑ 25,0 25,1 CHAVES, Alaor Silvério (2001). Física. Eletromagnetismo. 2. Rio de Janeiro: Reichmann & Affonso. p. 158-159. ISBN 85-87148-51-6
- ↑ Joe Rosen (1 de janeiro de 2009). Encyclopedia of Physics. [S.l.]: Infobase Publishing. 149 páginas. ISBN 978-1-4381-1013-4. Consultado em 29 de setembro de 2012
Ligações externas
Bibliografia
- Peter William Atkins e Loretta Jones, Princípios de Química, Bookman, Porto Alegre, 2001.
- José Roberto Castilho Piqueira e Luís Ricardo Arruda de Andrade, Física 2 - Eletricidade Básica/Eletromagnetismo, Gráfica e Editora Angloaa Ltda, São Paulo, 2002.
- Ference Jr., M., Eletromagnetismo, Editora Blücher Ltda, CE Stevaux.





























 " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">


