Função (matemática)

 Nota: Para outros significados de Função, veja Função (desambiguação).

Representação em diagrama de Venn de uma função ${\textstyle f:A\to B}$.

Uma função é uma relação de um conjunto ${\textstyle A}$ com um conjunto ${\textstyle B}$, onde cada elemento de ${\textstyle A}$ se relaciona unicamente com um elemento de ${\textstyle B}$. Usualmente, denotamos uma tal função por ${\textstyle f:A\to B}$, ${\textstyle y=f(x)}$, onde ${\textstyle f}$ é o nome da função, ${\textstyle A}$ é chamado de conjunto de partida, ${\textstyle B}$ é chamado de contradomínio e ${\textstyle y=f(x)}$ expressa a lei de correspondência (relação) dos elementos ${\textstyle x\in A}$ com os elementos ${\textstyle y\in B}$. Conforme suas características, as funções são agrupas em várias categorias, entre as principais temos: função sobrejetora, função injetora, função bijetora, função trigonométrica, função lineare, função modular, função quadrática, função exponencial, função logarítmica, função polinomial, dentre inúmeras outras.

Conceito

As funções são definidas por certas relações. Por causa de sua generalidade, as funções aparecem em muitos contextos matemáticos e muitas áreas da matemática baseiam-se no estudo de funções. Deve-se notar que as palavras "função", "mapeamento", "mapa" e "transformação" são geralmente usadas como termos equivalentes. Além disso pode-se ocasionalmente se referir a funções como "funções bem definidas" ou "funções totais". O conceito de uma função é uma generalização da noção comum de fórmula matemática. As funções descrevem relações matemáticas especiais entre dois elementos. Intuitivamente, uma função é uma maneira de associar a cada valor do argumento ${\textstyle x}$ (às vezes denominado variável independente) um único valor da função ${\textstyle f(x)}$ (também conhecido como variável dependente). Isto pode ser feito através de uma equação, um relacionamento gráfico, diagramas representando os dois conjuntos, uma regra de associação, uma tabela de correspondência, etc.. Muitas vezes, é útil associar cada par de elementos relacionados pela função com um ponto em um espaço adequado (por exemplo, no espaço ${\textstyle \mathbb {R} ^{2}}$, geometricamente representado no plano cartesiano). Neste caso, a exigência de unicidade da imagem (valor da função) implica um único ponto para cada entrada ${\textstyle x}$ (valor do argumento).

Assim como a noção intuitiva de funções não se limita a cálculos usando números individuais, a noção matemática de funções não se limita a cálculos e nem mesmo a situações que envolvam números. De forma geral, uma função liga um domínio (conjunto de valores de entrada) com um segundo conjunto, o contradomínio ou codomínio (conjunto de valores de saída), de tal forma que a cada elemento do domínio está associado exatamente um elemento do contradomínio. O conjunto dos elementos ${\textstyle y}$ do contradomínio para os quais existe pelo menos um ${\textstyle x}$ no domínio tal que ${\textstyle y=f(x)}$ (i.e., ${\textstyle x}$ se relaciona com ${\textstyle y}$), é o conjunto imagem ou chamado simplesmente de imagem da função.

Definição formal

Sejam dados os conjuntos ${\textstyle A}$, ${\textstyle B}$, uma relação ${\textstyle f:A\to B}$ e o conjunto dos pares ordenados ${\textstyle \mathbb {P} =\{(a,b)\in A\times B;a~{\mbox{se relaciona com}}~b\}}$. Dizemos que ${\textstyle f}$ é uma função se, e somente se, para todos ${\textstyle b_{1}\neq b_{2}\in B}$ com ${\textstyle (a_{1},b_{1}),(a_{2},b_{2})\in \mathbb {P} }$, temos ${\textstyle a_{1}\neq a_{2}}$. Ou, em outras palavras, para todo ${\textstyle a\in A}$ existe no máximo um ${\textstyle b\in B}$ tal que ${\textstyle a}$ se relaciona com ${\textstyle b}$. Assim sendo, escrevemos ${\textstyle b=f(a)}$ quando ${\textstyle a}$ se relaciona com ${\textstyle b}$ por ${\textstyle f}$. O conjunto ${\textstyle A}$ é chamado de conjunto de partida e ${\textstyle B}$ é chamado de contradomínio da função ${\textstyle f}$.

Outra maneira de dizer isto é afirmar que ${\textstyle f}$ é uma relação binária entre os dois conjuntos tal que ${\textstyle f}$ é unívoca, i.e. se ${\textstyle b=f(a)}$ e ${\textstyle c=f(a)}$, então ${\textstyle b=c}$. Algumas vezes, na definição de função, impõe-se todo o elemento do conjunto ${\textstyle A}$ se relaciona com algum elemento de ${\textstyle B}$.

Exemplos:

Vejamos as seguintes relações ${\textstyle f:X\to Y}$:

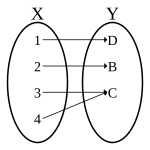
	Esta não é uma função, pois o elemento ${\textstyle 3\in X}$ é associado (se relaciona) com dois elementos ${\textstyle Y}$, a saber com ${\textstyle c,d\in Y}$. Esta é, entretanto, um exemplo das chamadas funções multivaloradas.
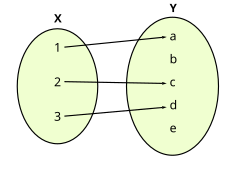
	Este é um exemplo de uma função dita parcial (função parcial), pois há pelo menos um elemento no conjunto de partida, a saber ${\textstyle 1\in X}$, que não se relaciona com nenhum elemento do contradomínio (conjunto ${\textstyle Y}$).
	Este é um exemplo de uma função dita discreta (veja, função discreta). Sua lei de correspondência pode ser escrita da seguinte forma: $f(x)=\left\{{\begin{matrix}a,&{\mbox{se }}x=1\\c,&{\mbox{se }}x=2\\d,&{\mbox{se }}x=3.\end{matrix}}\right.$

Exemplo de aplicação

Podemos usar uma função para modelar o número de indivíduos em uma população de acordo com o tempo (modelos de crescimento demográfico). Por exemplo, denotando o tempo por $t$ e o número de indivíduos em um dado tempo ${\textstyle t}$ por ${\textstyle y}$, escrevemos ${\textstyle N:\mathbb {R} ^{+}\to \mathbb {N} }$, ${\textstyle y=N(t)}$. Assim, temos abstratamente modelado o número de indivíduos (variável dependente) em função do tempo (variável independente). Aqui, o nome da função foi arbitrariamente escolhido como ${\textstyle N}$, o conjunto de partida é o conjunto dos números reais não negativos (assumindo que o tempo é contínuo e não negativo) e o contradomínio é o conjunto dos números naturais (assumindo que o número de indivíduos é sempre um número inteiro não negativo).

Elementos de uma função

Da definição, temos que uma função tem um nome, um conjunto de partida, um contradomínio (conjunto de chegada) e uma lei de correspondência. Por exemplo, denotamos ${\textstyle f:X\to Y}$, ${\textstyle y=f(x)}$, onde ${\textstyle f}$ é o nome da função, ${\textstyle X}$ é seu conjunto de partida, ${\textstyle Y}$ é seu contradomínio e ${\textstyle y=f(x)}$ denota sua lei de correspondência.

Representação em diagrama de Venn da função ${\textstyle f:C\to CD}$, ${\textstyle y=x^{2}}$. A imagem de ${\textstyle f}$ está delineada por uma linha tracejada.

Em muitos casos, nem todos os elementos do conjunto de partida se relacionam com algum elemento do contradomínio. Aqueles que se relacionam são elementos do chamado domínio da função. Mais precisamente, o domínio de uma função ${\textstyle f:X\to Y}$, ${\textstyle y=f(x)}$, é o conjunto:

$$Dom(f):=\{x\in X;\exists y\in Y~{\mbox{com}}~y=f(x)\}\subset X$$

Também, geralmente, nem todos os elementos do contradomínio se relacionam com algum elemento do conjunto de partida. Aqueles que se relacionam são elementos da chamada imagem da função. A imagem de uma função ${\textstyle f:X\to Y}$, ${\textstyle y=f(x)}$, é o conjunto:

$$Im(f):=\{y\in Y;\exists x\in X~{\mbox{com}}~y=f(x)\}\subset Y$$

Exemplo

Seja ${\textstyle f:C\to CD}$, ${\textstyle y=x^{2}}$, onde o conjunto de partida é dada por${\textstyle C=\{-3,-2,-1,0\}}$ e o contradomínio por${\textstyle CD=\{0,1,2,\dotsc ,9\}}$. Pela lei de correspondência, vemos que, neste caso, ${\textstyle Dom(f)=C}$ e ${\textstyle Im(f)=\{0,1,4,9\}}$. Veja a ilustração.

Gráfico de uma função

Esboço do gráfico de uma função arbitrária de uma variável com representação do par ordenado ${\textstyle (a,f(a))}$.

Ver artigo principal: Gráficos de função

O gráfico de uma função ${\textstyle f:X\to Y}$, ${\textstyle y=f(x)}$, é o conjunto:

$$Graf(f):=\{(x,y)\in X\times Y;y=f(x)\}$$

i.e, é o conjunto dos pares ordenados ${\textstyle (x,y)}$ tal que ${\textstyle y=f(x)}$.

Quando possível, usualmente fazemos uma representação geométrica do gráfico da função. Tal representação é usualmente chamada de esboço do gráfico da função (ou, simplesmente gráfico, quando subentendido).

Popularmente, temos os gráficos de funções de uma variável, para as quais seu esboço é dado pelo conjunto de pontos ${\textstyle (x,f(x))}$ no plano cartesiano (veja a ilustração). Neste caso, usualmente as variáveis independentes são chamadas de abcissas e marcadas sobre o eixo horizontal (chamado de eixo das abcissas). As variáveis dependentes são chamadas de ordenadas e marcadas sobre o eixo vertical (chamado de eixo das ordenadas).

Tipos de funções

Dependendo do tipo de regra que associa os elementos do domínio aos elementos do contradomínio de uma função, ela pode receber nomes específicos. Por exemplo,

• Se a regra que associa o domínio ao contradomínio é um polinômio, então a função é dita uma função polinomial. Exemplos de funções polinomiais são a função linear e a função quadrática.
• Se a regra eleva o logaritmo neperiano pelos elementos do domínio, então a função é dita exponencial.

Os tipos de funções podem ser classificados de acordo com o seu comportamento com relação à regra uma única saída para cada entrada. Como não foi dito nada sobre as entradas, ou se as saídas tem que ser únicas temos que resolver estas ambiguidades. Ao fazer isto encontramos apenas três tipos de classes de funções, e classe é empregado aqui como classificação mesmo e não como classe de equivalência.

Tipo de função	Característica da função	Conjunto imagem	Explicação visual	Exemplo	Admite função inversa? É inversível?
Injetora ou injetiva	Cada elemento da imagem está associado a apenas um elemento do domínio, isto é, quando $x$ ≠ $y$ no domínio tem-se $f(x)$ ≠ $f(y)$ no contradomínio.	Pode haver elementos do contradomínio que não pertençam à imagem da função.		A função $f:$ $N$ $\rightarrow$ $N$ dada por $f(x)=2x$, é injetiva porque números distintos possuem dobros distintos.	Nem sempre, mas sempre admite inversa à esquerda.
Sobrejetora ou sobrejetiva	Todos os elementos do contradomínio estão associados a algum elemento do domínio.	O conjunto imagem é igual ao conjunto contradomínio		A função $f:$ $R$ $\rightarrow$ $R$ dada por $f(x)=x^{2}$, não é sobrejetiva, pois o número -1 é elemento do contradomínio $R$ e não é imagem de qualquer elemento do domínio.	Nem sempre, mas sempre admite inversa à direita.
Bijetora ou bijetiva	São ao mesmo tempo sobrejetoras e injetoras, isto é, cada elemento do domínio está associado a um único elemento do contradomínio e vice-versa.	O conjunto imagem é igual ao conjunto contradomínio		A função $f:$ $N$ $\rightarrow$ $N$ dada por $f(x)=x$, é bijetiva porque é sobrejetiva e injetiva ao mesmo tempo. Exemplo: função identidade	Sim, sempre; imagem igual ao contradomínio vira domínio e vice-versa.

Funções implícitas e explicitas

O tipo de função mais comum é aquele onde o argumento e o valor da função são ambos numéricos, o relacionamento entre os dois é expresso por uma fórmula e o valor da função é obtido através da substituição direta dos argumentos. Considere o exemplo:

$f(x)=x^{2}$

que associa a cada x o seu quadrado. Uma generalização direta é permitir funções que dependam não só de um único valor, mas de vários. Por exemplo:

$g(x,y)=xy,$

recebe dois números x e y e associa a eles o seu produto, xy. De acordo com o modo como uma função é especificada, ela é chamada de função explícita (como acima) ou de função implícita, como em

$xf(x)=1,$

que define implicitamente a função

$f(x)={\frac {1}{x}}.$

Composição de funções

São as funções em que o conjunto imagem de uma função $f(x)$ serve de domínio para uma outra função $g(x),$ que por sua vez gera um conjunto imagem A. A função composta é uma expressão que, dado um determinado número do domínio de $f(x),$ nos leva diretamente ao conjunto imagem A.Por exemplo, dadas as funções que se seguem:

$f(x)=2x+3$ e $g(x)=x-1$

uma função composta pode ser:

$g(f(x))=2x+2$

Observa-se que f(x) transforma-se em variável de g(x). Ou seja, g(x)= ƒ(x)-1. Temos que, g(f(x)) = (2x+3)-1. Logo g(f(x)) = 2x+2. Existem várias maneiras de se criar funções compostas. Podemos fazer $f(g(x)),$ $f(f(x)),$ etc. Note que o conjunto imagem de uma função serve sempre de domínio para a outra.

Outras propriedades

Há muitas outras classes especiais de funções que são importantes em áreas ou aplicações específicas da matemática. Alguns desses tipos de funções são listados a seguir.

• injetiva
• sobrejetiva
• bijetiva
• contínua
• diferenciável, integrável
• linear, polinomial, racional
• algébrica, transcendental
• trigonométrica
• fractal
• par ou ímpar
• convexa, côncava monótona, unimodal
• holomorfa, meromorfa, inteira
• vetorial
• computável

História

O uso de "função" como um termo matemático foi iniciado por Leibniz, em uma carta de 1673, para designar uma quantidade relacionada a uma curva, tal como a sua inclinação em um ponto específico. As funções que Leibniz considerou são atualmente chamadas de funções diferenciáveis. Em relação a este tipo de função, pode-se falar em limites e derivadas. Estes conceitos são medidas dos valores de saída ou de sua variação em relação aos valores de entrada, e formam a base do cálculo.

A palavra função foi, posteriormente, usada por Euler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos. Com o tempo foi-se ampliando a definição de funções. Os matemáticos foram capazes de estudar "estranhos" objetos matemáticos tais como funções que não são diferenciáveis em qualquer de seus pontos. Tais funções, inicialmente tidas como puramente imaginárias e chamadas genericamente de "monstros", foram já no final do século XX, identificadas como importantes para a construção de modelos físicos de fenômenos tais como o movimento Browniano.

Durante o Século XIX, os matemáticos começaram a formalizar todos os diferentes ramos da matemática. Weierstrass defendia que se construisse o cálculo infinitesimal sobre a Aritmética ao invés de sobre a Geometria, o que favorecia a definição de Euler em relação à de Leibniz. Mais para o final do século, os matemáticos começaram a tentar formalizar toda a Matemática usando Teoria dos conjuntos, e eles conseguiram obter definições de todos os objetos matemáticos em termos do conceito de conjunto. Foi Dirichlet quem criou a definição "formal" de função moderna. Na definição de Dirichlet, uma função é um caso especial de uma relação. Relação é um conjunto de pares ordenados, onde cada elemento do par pertence a um dos conjuntos relacionados. Nas relações não existem restrições quanto à lei de correspondência entre os elementos dos conjuntos, já para as funções é costume introduzir restrições. Na maioria dos casos de interesse prático, entretanto, as diferenças entre as definições moderna e de Euler são desprezáveis.

Ver também

• Função implícita
• Funcional
• Composição de funções
• Programação funcional
• Funtor
• Anexo:Lista de funções matemáticas
• Função generalizada

Referências

Bibliografia

• Ávila, Geraldo Severo de Souza. (2005). Análise matemática para licenciatura. São Paulo. Edgard Blücher. ISBN 85-212-0371-3.
• Barboni, Ayrton; Paulette, Walter. (2007). Fundamentos de Matemática: Cálculo e Análise. Editora LTC. ISBN 978-85-216-1546-0.

Ligações externas

• Funções e Gráficos: um curso introdutório da UFRGS
• Relações e Funções
• Explicação de funções em 19 páginas pelo Grupo de Matemática da Universidade Técnica de Lisboa