imported>E2mb0t m (e2m - robot Adding:el,it,da,es,et,id,zh,sv,ja,he Modifying:en) |
imported>Elilopes (→Ver também: se então (informática)) |
||
| Linha 1: | Linha 1: | ||
{{ | {{mais notas|data=Janeiro de 2011}} | ||
{{ver desambiguação|Função}} | |||
[[Imagem:Function color example 3.svg|thumb|Uma função que associa cada uma das formas coloridas à sua cor.]] | |||
Uma '''função''' é uma [[Relação (matemática)|relação]] de um [[conjunto]] <math display="inline">A</math> com um conjunto <math display="inline">B.</math> Usualmente, denotamos uma tal função por <math display="inline">f:A\to B,</math> <math display="inline">y = f(x),</math> onde <math display="inline">f</math> é o nome da função, <math display="inline">A</math> é chamado de domínio, <math display="inline">B</math> é chamado de imagem e <math display="inline">y = f(x)</math> expressa a lei de correspondência (relação) dos elementos <math display="inline">x\in A</math> com os elementos <math display="inline">y\in B.</math> Conforme suas características, as funções são agrupadas em várias categorias, entre as principais temos: [[função trigonométrica]], [[função linear|função afim (ou função polinomial do 1° grau)]], [[função modular]], [[função quadrática]] (ou função polinomial do 2° grau), [[função exponencial]], [[função logarítmica]], [[função polinomial]], dentre inúmeras outras.<ref>STEWART, James. Cálculo Vol. I - 4ª edição. São Paulo: Pioneira Thomson Learning, 2002. Página 12.</ref><ref>FRANK AYRES, Philip A. Schmidt. Matemática para Ensino Superior - 3ª edição. São Paulo: Editora Artmed, 2003. Página 16.</ref><ref name=":0">{{citar livro|titulo=Fundamentos de Matemática Elementar: conjuntos e funções|ultimo=Iezzi|primeiro=Gelson|editora=Atual|ano=1977|local=São Paulo|paginas=73-74A, 179A-180A|acessodata=}}</ref> | |||
== Conceito == | |||
As funções são definidas por certas relações. Por causa de sua generalidade, as funções aparecem em muitos contextos matemáticos e muitas áreas da matemática baseiam-se no estudo de funções. Deve-se notar que as palavras "função", "mapeamento", "mapa" e "transformação" são geralmente usadas como termos equivalentes. Além disso pode-se ocasionalmente se referir a funções como "funções bem definidas" ou "funções totais". O conceito de uma '''função''' é uma generalização da noção comum de [[fórmula|fórmula matemática]]. As funções descrevem [[Relação (matemática)|relações matemáticas]] especiais entre dois elementos. Intuitivamente, uma função é uma maneira de associar a cada valor do argumento <math display="inline">x</math> (às vezes denominado ''variável independente'') um '''único''' valor da função <math display="inline">f(x)</math> (também conhecido como ''variável dependente''). Isto pode ser feito através de uma [[equação]], um relacionamento gráfico, diagramas representando os dois conjuntos, uma regra de associação, uma tabela de correspondência, etc.. Muitas vezes, é útil associar cada par de elementos relacionados pela função com um ponto em um espaço adequado (por exemplo, no [[Espaço matemático|espaço]] <math display="inline">\mathbb{R}^2,</math> geometricamente representado no [[Sistema de coordenadas cartesiano|plano cartesiano]]). Neste caso, a exigência de unicidade da imagem (valor da função) implica um único ponto para cada entrada <math display="inline">x</math> (valor do argumento).<ref name=":0" /><ref name="stewart-02">STEWART, James. Cálculo Vol. I - 4ª edição. São Paulo: Pioneira Thomson Learning, 2002.</ref><ref name="Ayres-03">FRANK AYRES, Philip A. Schmidt. Matemática para Ensino Superior - 3ª edição. São Paulo: Editora Artmed, 2003.</ref> | |||
== | Assim como a noção intuitiva de funções não se limita a cálculos usando números individuais, a noção matemática de funções não se limita a cálculos e nem mesmo a situações que envolvam números. De forma geral, uma função liga um domínio (conjunto de valores de entrada) com um segundo conjunto, o [[contradomínio]] ou '''codomínio''' (conjunto de valores de saída), de tal forma que a cada elemento do domínio está associado exatamente um elemento do contradomínio. O conjunto dos elementos <math display="inline">y</math> do contradomínio para os quais existe pelo menos um <math display="inline">x</math> no domínio tal que <math display="inline">y=f(x)</math> (i.e., <math display="inline">x</math> se relaciona com <math display="inline">y</math>), é o [[conjunto imagem]] ou chamado simplesmente de imagem da função.<ref name="Ayres-03" /> | ||
== Definição formal == | |||
Sejam dados os conjuntos <math display="inline">A,</math> <math display="inline">B,</math> uma relação <math display="inline">f:A\to B</math> e o conjunto dos pares ordenados <math display="inline">\mathbb{P} = \{(a,b)\in A\times B; a~\mbox{se relaciona com}~b~\mbox{por}~f\}.</math> Dizemos que <math display="inline">f</math> é uma função se, e somente se, para todos <math display="inline">b_1 \neq b_2\in B</math> com <math display="inline">(a_1, b_1), (a_2, b_2)\in \mathbb{P},</math> temos <math display="inline">a_1\neq a_2 | |||
.</math> Ou, em outras palavras, para todo <math display="inline">a\in A</math> existe no máximo um <math display="inline">b\in B | |||
</math> tal que <math display="inline">a</math> se relaciona com <math display="inline">b.</math> <ref name=":0" /> Assim sendo, escrevemos <math display="inline">b = f(a)</math> quando <math display="inline">a</math> se relaciona com <math display="inline">b</math> por <math display="inline">f.</math> O conjunto <math display="inline">A</math> é chamado de conjunto de partida e <math display="inline">B</math> é chamado de contradomínio da função <math display="inline">f.</math> | |||
Outra maneira de dizer isto é afirmar que <math display="inline">f</math> é uma [[relação binária]] entre os dois conjuntos tal que <math display="inline">f</math> é '''unívoca,''' i.e. se <math display="inline">b = f(a)</math> e <math display="inline">c = f(a),</math> então <math display="inline">b = c.</math> Algumas vezes, na definição de função, impõe-se que todo o elemento do conjunto <math display="inline">A</math> se relaciona com algum elemento de <math display="inline">B.</math> | |||
=== Exemplos === | |||
Vejamos as seguintes relações <math display="inline">f:X\to Y:</math> | |||
{| | |||
|- | |||
| [[Imagem:Naofuncao1.png|230px]] | |||
| Esta não é uma função, pois o elemento <math display="inline">3\in X</math> é associado (se relaciona) com dois elementos <math display="inline">Y,</math> a saber com <math display="inline">c,d\in Y.</math> Esta é, entretanto, um exemplo das chamadas [[função multivalorada|funções multivaloradas]]. | |||
|- | |||
| [[Imagem:Naofuncao2.png|230px]] | |||
| Este é um exemplo de uma função dita parcial ([[função parcial]]), pois há pelo menos um elemento no conjunto de partida, a saber <math display="inline">1\in X,</math> que não se relaciona com nenhum elemento do contradomínio (conjunto <math display="inline">Y</math>). | |||
|- | |||
| [[Imagem:Funcao venn.svg|230px]] | |||
| Este é um exemplo de uma função dita discreta (veja, [[função discreta]]). Sua lei de correspondência pode ser escrita da seguinte forma: | |||
<math display="block">f(x)=\left\{\begin{matrix} a, & \mbox{se }x=1 \\ c, & \mbox{se }x=2 \\ d, & \mbox{se }x=3. \end{matrix}\right.</math> | |||
|} | |||
== Exemplo de aplicação == | |||
:<math> | Podemos usar uma função para modelar o número de indivíduos em uma população de acordo com o tempo ([[Crescimento demográfico (equação diferencial)|modelos de crescimento demográfico]]). Por exemplo, denotando o tempo por <math>t</math> e o número de indivíduos em um dado tempo <math display="inline">t</math> por <math display="inline">y,</math> escrevemos <math display="inline">N:\mathbb{R}^+\to \mathbb{N},</math> <math display="inline">y = N(t).</math> Assim, temos abstratamente modelado o número de indivíduos (variável dependente) em função do tempo (variável independente). Aqui, o nome da função foi arbitrariamente escolhido como <math display="inline">N,</math> o conjunto de partida é o conjunto dos [[Número real|números reais]] não negativos (assumindo que o tempo é contínuo e não negativo) e o contradomínio é o conjunto dos [[números naturais]] (assumindo que o número de indivíduos é sempre um [[número inteiro]] não negativo). | ||
== Elementos de uma função == | |||
Da definição, temos que uma função tem um nome, um conjunto de partida, um contradomínio (conjunto de chegada) e uma lei de correspondência. Por exemplo, denotamos <math display="inline">f:X\to Y,</math> <math display="inline">y = f(x),</math> onde <math display="inline">f</math> é o nome da função, <math display="inline">X</math> é seu conjunto de partida, <math display="inline">Y</math> é seu contradomínio e <math display="inline">y = f(x)</math> denota sua lei de correspondência. | |||
Em muitos casos, nem todos os elementos do conjunto de partida se relacionam com algum elemento do contradomínio. Aqueles que se relacionam são elementos do chamado [[Domínio (matemática)|domínio da função]]. Mais precisamente, o domínio de uma função <math display="inline">f:X\to Y,</math> <math display="inline">y = f(x),</math> é o conjunto:<math display="block">Dom(f) := \{x\in X; \exists y\in Y ~ \mbox{com} ~ y = f(x)\}\subset X</math>Também, geralmente, nem todos os elementos do contradomínio se relacionam com algum elemento do conjunto de partida. Aqueles que se relacionam são elementos da chamada [[Imagem (matemática)|imagem da função]]. A imagem de uma função <math display="inline">f:X\to Y,</math> <math display="inline">y = f(x),</math> é o conjunto:<math display="block">Im(f) := \{y\in Y; \exists x\in X ~\mbox{com} ~ y = f(x)\}\subset Y</math> | |||
:<math> | |||
:<math>f(x) | |||
=== Exemplo === | |||
Seja <math display="inline">f:C\to CD,</math> <math display="inline">y = x^2,</math> onde o conjunto de partida é dada por <math display="inline">C = \{-3,-2,-1,0\}</math> e o contradomínio por<math display="inline">CD = \{0,1,2,\dotsc,9\}.</math> Pela lei de correspondência, vemos que, neste caso, <math display="inline">Dom(f) = C</math> e <math display="inline">Im(f) = \{0,1,4,9\}.</math> Veja a ilustração. | |||
[[Imagem:funcoes x2.svg|thumb|250px|Representação em diagrama de Venn da função <math display="inline">f:C\to CD,</math> <math display="inline">y = x^2.</math> A imagem de <math display="inline">f</math> está delineada por uma linha tracejada.]] | |||
== Gráfico de uma função == | |||
[[Ficheiro:Graph of a function.svg|miniaturadaimagem|Esboço do gráfico de uma função arbitrária de uma variável com representação do par ordenado <math display="inline">(a,f(a)).</math>]] | |||
{{Artigo principal|[[Gráfico#Gráficos de função|Gráficos de função]]}} | |||
O gráfico de uma função <math display="inline">f:X\to Y,</math> <math display="inline">y = f(x),</math> é o conjunto:<math display="block">Graf(f) := \{(x,y)\in X\times Y; y = f(x)\}</math>i.e, é o conjunto dos [[Par ordenado|pares ordenados]] <math display="inline">(x,y)</math> tal que <math display="inline">y = f(x).</math> | |||
Quando possível, usualmente fazemos uma representação geométrica do gráfico da função. Tal representação é usualmente chamada de esboço do gráfico da função (ou, simplesmente gráfico, quando subentendido). | |||
Popularmente, temos os gráficos de funções de uma variável, para as quais seu esboço é dado pelo conjunto de pontos <math display="inline">(x,f(x))</math> no plano cartesiano (veja a ilustração). Neste caso, usualmente as variáveis independentes são chamadas de [[Abscissa|abcissas]] e marcadas sobre o eixo horizontal (chamado de eixo das abcissas). As variáveis dependentes são chamadas de [[ordenada]]s e marcadas sobre o eixo vertical (chamado de eixo das ordenadas). | |||
== Classificação quando a imagem == | |||
Funções são usualmente classificadas quanto a sua imagem como: [[Função injectiva|funções injetoras]], [[Função sobrejectiva|funções sobrejetoras]] e [[Função bijectiva|funções bijetoras]]. | |||
Seja dada a função <math display="inline">f:X\to Y,</math> <math display="inline">y = f(x).</math> Por definição, <math display="inline">f</math> é injetora (ou injetiva) se, e somente se, para todos <math display="inline">x_1\neq x_2 \in Dom(f)</math> temos <math display="inline">f(x_1)\neq f(x_2).</math> A função <math display="inline">f</math> é dita sobrejetora (ou sobrejetiva) quando <math display="inline">Im(f) = Y.</math> Por fim, uma função injetora e sobrejetora é dita ser bijetora (ou bijetiva). Veja a seguinte tabela. | |||
{| class="wikitable" | |||
|- | |||
! style="width: 70px;" | Tipo de função | |||
! style="width: 250px;" | Característica da função | |||
! style="width: 140px;" | Conjunto imagem | |||
! Explicação visual | |||
! style="width: 180px;" |Exemplo | |||
! Admite [[função inversa]]? É inversível? | |||
|- | |||
| '''Injetora ou injetiva''' | |||
| Cada elemento da imagem está associado a apenas um elemento do domínio, isto é, quando ''<math>x</math> ≠ <math>y</math>'' no domínio tem-se ''<math>f(x)</math> ≠ <math>f(y)</math>'' no contradomínio. | |||
| Pode haver elementos do contradomínio que não pertençam à imagem da função. | |||
| [[Imagem:Funcao venn.svg|180px|center]] | |||
| A função <math>f:</math> <math>N</math> <math>\rightarrow</math> <math>N</math> dada por ''<math>f(x)=2x</math>'', é injetiva porque números distintos possuem dobros distintos. | |||
| Nem sempre, mas sempre admite inversa à esquerda. | |||
|- | |||
| '''Sobrejetora ou sobrejetiva''' | |||
| Todos os elementos do contradomínio estão associados a algum elemento do domínio. | |||
| O conjunto imagem é igual ao conjunto contradomínio | |||
| [[Imagem:Surjection.svg|150px|center]] | |||
| A função <math>f:\mathbb{R}\to\mathbb{R},</math> ''<math display="inline">f(x)=x</math>'', é sobrejetiva. | |||
| Nem sempre, mas sempre admite inversa à direita. | |||
|- | |||
| '''Bijetora ou bijetiva''' | |||
| São ao mesmo tempo sobrejetoras e injetoras, isto é, cada elemento do domínio está associado a um único elemento do contradomínio e vice-versa. | |||
| O conjunto imagem é igual ao conjunto contradomínio | |||
| [[Imagem:Bijection.svg|150px|center]] | |||
| A função <math display="inline">f:\mathbb{N}\to\mathbb{N},</math> ''<math>f(x)=x</math>'', é bijetiva. | |||
| Sim. | |||
|} | |||
== Funções implícitas e explicitas == | |||
Dizemos que uma função <math display="inline">f:X\to Y</math> é definida de forma explícita (função explícita) quando seus valores <math display="inline">y</math> podem ser expressados pela variável independente <math display="inline">x,</math> i.e., quando temos uma relação da forma <math display="inline">y = f(x).</math> Por outro lado, dizemos que uma tal função é definida de forma implícita (função implícita) quando a relação entre as variáveis dependente e independente é dada como <math display="inline">F(x,y) = 0,</math> onde <math display="inline">F(x,y)</math> denota uma expressão envolvendo <math display="inline">x | |||
</math> e <math display="inline">y.</math> <ref>{{citar livro|titulo=Handbook of Mathematics|ultimo=Bronshtein|primeiro=I.N.|editora=Springer|ano=2007|local=Berlin|paginas=120|acessodata=}}</ref> | |||
==== Exemplo ==== | |||
Seja <math display="inline">G:\mathbb{R}^2\to\mathbb{R}</math> dada por <math display="inline">G(x,y) = xy.</math> Isto é, a função que toma dois valores reais e os associa ao produto entre eles. Trata-se de uma função explícita. Agora, a equação <math display="inline">xy - 1 = 0,</math> define implicitamente a função <math display="inline">f:\mathbb{R^*}\to\mathbb{R}</math> que associa um número real não nulo <math display="inline">x</math> ao seu inverso. Ou seja, tal função <math display="inline">f</math> está, aqui, definida implicitamente por <math display="inline">F(x,y) := xy - 1 = 0.</math> Notamos que neste caso em particular, podemos definir a função <math display="inline">f</math> de forma explícita, escrevendo <math display="inline">f(x) = \frac{1}{x}.</math> | |||
== Composição de funções == | |||
{{Artigo principal|[[Composição de funções]]}} | |||
Dadas uma função <math display="inline">f:A\to B,</math> <math display="inline">y = f(x)</math> e uma função <math display="inline">g:C\to D,</math> <math display="inline">y = g(x)</math> com <math display="inline">Im(g)\subset Dom(f),</math> definimos a função composta de <math display="inline">f | |||
</math> com <math display="inline">g</math> por <math display="inline">(f\circ g):C\to B,</math> <math display="inline">(f\circ g)(x) = f(g(x)).</math> Analogamente, quando <math display="inline">Im(f)\subset Dom(g)</math> também podemos definir a função composta de <math display="inline">g</math> com <math display="inline">f</math> dada por <math display="inline">(g\circ f):A\to D,</math> <math display="inline">(g\circ f)(x) = g(f(x)).</math> <ref name=":0" /> | |||
== | ==== Exemplo ==== | ||
Considere as seguintes funções <math display="inline">f:\mathbb{R}\to \mathbb{R}</math> e <math display="inline">g:\mathbb{R}\to\mathbb{R}</math> dada por: | |||
<math>f(x) = 2x + 3</math> e <math>g(x) = x - 1.</math> | |||
Notamos que <math display="inline">Im(f)\subset Dom(g)</math> e, portanto, podemos definir a função composta <math display="inline">(g\circ f):\mathbb{R}\to\mathbb{R}</math>por: | |||
<math display="block">(g\circ f)(x) = g(f(x)) = (2x + 3) - 1 = 2x + 2.</math> | |||
Também, como <math display="inline">Im(g)\subset Dom(f),</math> temos a composição <math display="inline">(f\circ g):\mathbb{R}\to\mathbb{R}</math> dada por: | |||
<math>(f\circ g)(x) = f(g(x)) = 2(x-1) + 3 = 2x + 1.</math> | |||
== Outras classificações == | |||
{{Anexo|Lista de funções matemáticas}} | |||
Função são classificadas quanto a uma séries de propriedades (características) além das já mencionadas. Alguns desses tipos de funções são listados a seguir. | |||
{{div col|3}} | |||
* [[Função algébrica]] | |||
* [[Função computável]] | |||
* [[função côncava]] | |||
* [[Função convexa]] | |||
* [[Função contínua]] | |||
* [[Função diferenciável]] | |||
* [[Função holomorfa]] | |||
* [[Função ímpar]] | |||
* [[Função inteira]] | |||
* [[Função integrável]] | |||
* [[Função inversa]] | |||
* [[Função linear]] | |||
* [[Função modular]] | |||
* [[Função meromorfa]] | |||
* [[Função monótona]] | |||
* [[Função par]] | |||
* [[Função polinomial]] | |||
* [[Função quadrática]] | |||
* [[Função racional]] | |||
* [[Função transcendental]] | |||
* [[Função trigonométrica]] | |||
* [[Função vetorial]] | |||
{{div col end}} | |||
== História == | |||
O conceito matemático de função emergiu no século XVII em conexão com o desenvolvimento do [[Cálculo Diferencial e Integral|Cálculo]].<ref>"The emergence of a notion of function as an individualized mathematical entity can be traced to the beginnings of infinitesimal calculus". ({{harvnb|Ponte |1992}})</ref><ref name="Kleiner 20092">{{citar livro||último =Kleiner|primeiro =Israel|capítulo=Evolution of the Function Concept: A Brief Survey|editor1=Marlow Anderson|editor2=Victor Katz|editor3=Robin Wilson|título=Who Gave You the Epsilon?: And Other Tales of Mathematical History|url=http://books.google.com/books?id=WwFMjsym9JwC&pg=PA15|ano=2009|publicado=MAA|isbn=978-0-88385-569-0|páginas=14–26}}</ref> O termo "função" foi introduzido por [[Gottfried Leibniz]] em uma de suas cartas, datada de 1673, na qual ele descreve a [[declividade]] de uma curva em um ponto específico.<ref name=":02">Eves dates Leibniz's first use to the year 1694 and also similarly relates the usage to "as a term to denote any quantity connected with a curve, such as the coordinates of a point on the curve, the slope of the curve, and so on" ({{harvnb|Eves |1990 |p=234}}).</ref> Na antiguidade, embora não se conheça o uso explícito de funções, tal conceito pode ser observado em alguns trabalhos percursores de filósofos e matemáticos medievais, como [[Nicole d'Oresme|Oresme]].<ref>"...although we do not find in [the mathematicians of Ancient Greece] the idea of functional dependence distinguished in explicit form as a comparatively independent object of study, nevertheless one cannot help noticing the large stock of functional correspondences they studied." ({{harvnb|Medvedev|1991|pages=29–30}})</ref> | |||
== | |||
[ | |||
Matemáticos do século XVII tratavam por funções aquelas definidas por [[Expressão matemática|expressões analíticas]].<ref name="Bourbaki20032">{{citar livro|autor =N. Bourbaki|título=Elements of Mathematics Functions of a Real Variable: Elementary Theory|url=http://books.google.com/books?id=dtYLvM02cRYC&pg=PA154|data=18 de setembro de 2003|publicado=Springer Science & Business Media|isbn=978-3-540-65340-0|páginas=154–}}</ref> Foi durante os desenvolvimentos rigorosos da [[Análise matemática|Análise Matemática]] por [[Karl Weierstrass|Weierstrass]] e outros, a reformulação da [[Geometria]] em termos da análise e a invenção da [[Teoria dos conjuntos|Teoria dos Conjuntos]] por Cantor, que se chegou ao conceito moderno e geral de uma função como um mapeamento unívoco de um conjunto em outro. Não há consenso sobre a quem se deva os créditos da noção moderna de função, sendo cotada os matemáticos [[Nikolai Lobachevsky]], [[Peter Gustav Lejeune Dirichlet]] e [[Dedekind]].<ref name=":12">"On the vanishing of trigonometric series," 1834 ({{harvnb| Lobachevsky |1951 |pages=31–80}}).</ref><ref name=":22">Über die Darstellung ganz willkürlicher Funktionen durch Sinus- und Cosinusreihen," 1837 ({{harvnb|Dirichlet|1889|pages=135–160}}).</ref><ref name=":32">"By a mapping φ of a set ''S'' we understand a law that assigns to each element ''s'' of ''S'' a uniquely determined object called the ''image'' of ''s'', denoted as φ(''s''). {{harvnb| Dedekind |1995|page=9}}</ref> | |||
: | |||
== Ver também == | |||
*[[Cálculo Diferencial e Integral|Cálculo diferencial e integral]] | |||
*[[Funcional]] | |||
*[[Função se então (informática)]] | |||
*[[Função generalizada]] | |||
*[[Funtor]] | |||
{{Referências}} | |||
=== Bibliografia === | |||
*Ávila, Geraldo Severo de Souza. (2005). ''[[Análise matemática]] para licenciatura''. São Paulo. Edgard Blücher. ISBN 85-212-0371-3. | |||
*Barboni, Ayrton; Paulette, Walter. (2007). ''Fundamentos de Matemática: Cálculo e Análise''. Editora LTC. ISBN 978-85-216-1546-0. | |||
*Iezzi, G; Murakami, C.. (2013). ''Fundamentos de Matemática Elementar: Conjuntos e Funções''. vol. 1, 9. ed., Atual Editora:São Paulo. ISBN 9788535716801. | |||
== Ligações externas == | |||
*[http://penta.ufrgs.br/edu/telelab/mundo_mat/cfuncao/fun_graf.htm Funções e Gráficos: um curso introdutório da UFRGS] | |||
*[http://www.matematica.pucminas.br/profs/web_walter/oficinas/Oficina022005.pdf Relações e Funções] | |||
*[http://math.tecnico.ulisboa.pt/textos/ppgmutlfuncoes.pdf Explicação de funções em 19 páginas pelo Grupo de Matemática da Universidade Técnica de Lisboa] | |||
{{Funções}} | |||
{{Análise}} | |||
{{Portal3|Matemática}} | |||
{{authority control}} | |||
[[Categoria:Teoria dos conjuntos]] | |||
[[Categoria:Funções matemáticas]] | |||
[[ | |||
[[ | |||
Edição atual tal como às 15h37min de 15 de dezembro de 2021
Uma função é uma relação de um conjunto com um conjunto Usualmente, denotamos uma tal função por onde é o nome da função, é chamado de domínio, é chamado de imagem e expressa a lei de correspondência (relação) dos elementos com os elementos Conforme suas características, as funções são agrupadas em várias categorias, entre as principais temos: função trigonométrica, função afim (ou função polinomial do 1° grau), função modular, função quadrática (ou função polinomial do 2° grau), função exponencial, função logarítmica, função polinomial, dentre inúmeras outras.[1][2][3]
Conceito
As funções são definidas por certas relações. Por causa de sua generalidade, as funções aparecem em muitos contextos matemáticos e muitas áreas da matemática baseiam-se no estudo de funções. Deve-se notar que as palavras "função", "mapeamento", "mapa" e "transformação" são geralmente usadas como termos equivalentes. Além disso pode-se ocasionalmente se referir a funções como "funções bem definidas" ou "funções totais". O conceito de uma função é uma generalização da noção comum de fórmula matemática. As funções descrevem relações matemáticas especiais entre dois elementos. Intuitivamente, uma função é uma maneira de associar a cada valor do argumento (às vezes denominado variável independente) um único valor da função (também conhecido como variável dependente). Isto pode ser feito através de uma equação, um relacionamento gráfico, diagramas representando os dois conjuntos, uma regra de associação, uma tabela de correspondência, etc.. Muitas vezes, é útil associar cada par de elementos relacionados pela função com um ponto em um espaço adequado (por exemplo, no espaço geometricamente representado no plano cartesiano). Neste caso, a exigência de unicidade da imagem (valor da função) implica um único ponto para cada entrada (valor do argumento).[3][4][5]
Assim como a noção intuitiva de funções não se limita a cálculos usando números individuais, a noção matemática de funções não se limita a cálculos e nem mesmo a situações que envolvam números. De forma geral, uma função liga um domínio (conjunto de valores de entrada) com um segundo conjunto, o contradomínio ou codomínio (conjunto de valores de saída), de tal forma que a cada elemento do domínio está associado exatamente um elemento do contradomínio. O conjunto dos elementos do contradomínio para os quais existe pelo menos um no domínio tal que (i.e., se relaciona com ), é o conjunto imagem ou chamado simplesmente de imagem da função.[5]
Definição formal
Sejam dados os conjuntos uma relação e o conjunto dos pares ordenados Dizemos que é uma função se, e somente se, para todos com temos Ou, em outras palavras, para todo existe no máximo um tal que se relaciona com [3] Assim sendo, escrevemos quando se relaciona com por O conjunto é chamado de conjunto de partida e é chamado de contradomínio da função
Outra maneira de dizer isto é afirmar que é uma relação binária entre os dois conjuntos tal que é unívoca, i.e. se e então Algumas vezes, na definição de função, impõe-se que todo o elemento do conjunto se relaciona com algum elemento de
Exemplos
Vejamos as seguintes relações

|
Esta não é uma função, pois o elemento é associado (se relaciona) com dois elementos a saber com Esta é, entretanto, um exemplo das chamadas funções multivaloradas. |

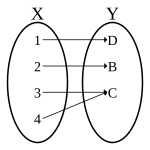
|
Este é um exemplo de uma função dita parcial (função parcial), pois há pelo menos um elemento no conjunto de partida, a saber que não se relaciona com nenhum elemento do contradomínio (conjunto ). |
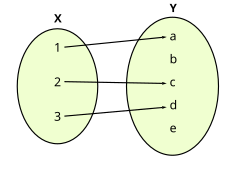
|
Este é um exemplo de uma função dita discreta (veja, função discreta). Sua lei de correspondência pode ser escrita da seguinte forma:
|
Exemplo de aplicação
Podemos usar uma função para modelar o número de indivíduos em uma população de acordo com o tempo (modelos de crescimento demográfico). Por exemplo, denotando o tempo por e o número de indivíduos em um dado tempo por escrevemos Assim, temos abstratamente modelado o número de indivíduos (variável dependente) em função do tempo (variável independente). Aqui, o nome da função foi arbitrariamente escolhido como o conjunto de partida é o conjunto dos números reais não negativos (assumindo que o tempo é contínuo e não negativo) e o contradomínio é o conjunto dos números naturais (assumindo que o número de indivíduos é sempre um número inteiro não negativo).
Elementos de uma função
Da definição, temos que uma função tem um nome, um conjunto de partida, um contradomínio (conjunto de chegada) e uma lei de correspondência. Por exemplo, denotamos onde é o nome da função, é seu conjunto de partida, é seu contradomínio e denota sua lei de correspondência.
Em muitos casos, nem todos os elementos do conjunto de partida se relacionam com algum elemento do contradomínio. Aqueles que se relacionam são elementos do chamado domínio da função. Mais precisamente, o domínio de uma função é o conjunto:
Exemplo
Seja onde o conjunto de partida é dada por e o contradomínio por Pela lei de correspondência, vemos que, neste caso, e Veja a ilustração.
Gráfico de uma função
O gráfico de uma função é o conjunto:
Quando possível, usualmente fazemos uma representação geométrica do gráfico da função. Tal representação é usualmente chamada de esboço do gráfico da função (ou, simplesmente gráfico, quando subentendido).
Popularmente, temos os gráficos de funções de uma variável, para as quais seu esboço é dado pelo conjunto de pontos no plano cartesiano (veja a ilustração). Neste caso, usualmente as variáveis independentes são chamadas de abcissas e marcadas sobre o eixo horizontal (chamado de eixo das abcissas). As variáveis dependentes são chamadas de ordenadas e marcadas sobre o eixo vertical (chamado de eixo das ordenadas).
Classificação quando a imagem
Funções são usualmente classificadas quanto a sua imagem como: funções injetoras, funções sobrejetoras e funções bijetoras. Seja dada a função Por definição, é injetora (ou injetiva) se, e somente se, para todos temos A função é dita sobrejetora (ou sobrejetiva) quando Por fim, uma função injetora e sobrejetora é dita ser bijetora (ou bijetiva). Veja a seguinte tabela.
| Tipo de função | Característica da função | Conjunto imagem | Explicação visual | Exemplo | Admite função inversa? É inversível? |
|---|---|---|---|---|---|
| Injetora ou injetiva | Cada elemento da imagem está associado a apenas um elemento do domínio, isto é, quando ≠ no domínio tem-se ≠ no contradomínio. | Pode haver elementos do contradomínio que não pertençam à imagem da função. | A função dada por , é injetiva porque números distintos possuem dobros distintos. | Nem sempre, mas sempre admite inversa à esquerda. | |
| Sobrejetora ou sobrejetiva | Todos os elementos do contradomínio estão associados a algum elemento do domínio. | O conjunto imagem é igual ao conjunto contradomínio | A função , é sobrejetiva. | Nem sempre, mas sempre admite inversa à direita. | |
| Bijetora ou bijetiva | São ao mesmo tempo sobrejetoras e injetoras, isto é, cada elemento do domínio está associado a um único elemento do contradomínio e vice-versa. | O conjunto imagem é igual ao conjunto contradomínio | A função , é bijetiva. | Sim. |
Funções implícitas e explicitas
Dizemos que uma função é definida de forma explícita (função explícita) quando seus valores podem ser expressados pela variável independente i.e., quando temos uma relação da forma Por outro lado, dizemos que uma tal função é definida de forma implícita (função implícita) quando a relação entre as variáveis dependente e independente é dada como onde denota uma expressão envolvendo e [6]
Exemplo
Seja dada por Isto é, a função que toma dois valores reais e os associa ao produto entre eles. Trata-se de uma função explícita. Agora, a equação define implicitamente a função que associa um número real não nulo ao seu inverso. Ou seja, tal função está, aqui, definida implicitamente por Notamos que neste caso em particular, podemos definir a função de forma explícita, escrevendo
Composição de funções
Dadas uma função e uma função com definimos a função composta de com por Analogamente, quando também podemos definir a função composta de com dada por [3]
Exemplo
Considere as seguintes funções e dada por:
e
Notamos que e, portanto, podemos definir a função composta por:
Outras classificações
- REDIRECIONAMENTO Predefinição:VT
Função são classificadas quanto a uma séries de propriedades (características) além das já mencionadas. Alguns desses tipos de funções são listados a seguir.
- Função algébrica
- Função computável
- função côncava
- Função convexa
- Função contínua
- Função diferenciável
- Função holomorfa
- Função ímpar
- Função inteira
- Função integrável
- Função inversa
- Função linear
- Função modular
- Função meromorfa
- Função monótona
- Função par
- Função polinomial
- Função quadrática
- Função racional
- Função transcendental
- Função trigonométrica
- Função vetorial
História
O conceito matemático de função emergiu no século XVII em conexão com o desenvolvimento do Cálculo.[7][8] O termo "função" foi introduzido por Gottfried Leibniz em uma de suas cartas, datada de 1673, na qual ele descreve a declividade de uma curva em um ponto específico.[9] Na antiguidade, embora não se conheça o uso explícito de funções, tal conceito pode ser observado em alguns trabalhos percursores de filósofos e matemáticos medievais, como Oresme.[10]
Matemáticos do século XVII tratavam por funções aquelas definidas por expressões analíticas.[11] Foi durante os desenvolvimentos rigorosos da Análise Matemática por Weierstrass e outros, a reformulação da Geometria em termos da análise e a invenção da Teoria dos Conjuntos por Cantor, que se chegou ao conceito moderno e geral de uma função como um mapeamento unívoco de um conjunto em outro. Não há consenso sobre a quem se deva os créditos da noção moderna de função, sendo cotada os matemáticos Nikolai Lobachevsky, Peter Gustav Lejeune Dirichlet e Dedekind.[12][13][14]
Ver também
Referências
- ↑ STEWART, James. Cálculo Vol. I - 4ª edição. São Paulo: Pioneira Thomson Learning, 2002. Página 12.
- ↑ FRANK AYRES, Philip A. Schmidt. Matemática para Ensino Superior - 3ª edição. São Paulo: Editora Artmed, 2003. Página 16.
- ↑ 3,0 3,1 3,2 3,3 Iezzi, Gelson (1977). Fundamentos de Matemática Elementar: conjuntos e funções. São Paulo: Atual. pp. 73–74A, 179A–180A
- ↑ STEWART, James. Cálculo Vol. I - 4ª edição. São Paulo: Pioneira Thomson Learning, 2002.
- ↑ 5,0 5,1 FRANK AYRES, Philip A. Schmidt. Matemática para Ensino Superior - 3ª edição. São Paulo: Editora Artmed, 2003.
- ↑ Bronshtein, I.N. (2007). Handbook of Mathematics. Berlin: Springer. 120 páginas
- ↑ "The emergence of a notion of function as an individualized mathematical entity can be traced to the beginnings of infinitesimal calculus". (Predefinição:Harvnb)
- ↑ Kleiner, Israel (2009). «Evolution of the Function Concept: A Brief Survey». In: Marlow Anderson; Victor Katz; Robin Wilson. Who Gave You the Epsilon?: And Other Tales of Mathematical History. [S.l.]: MAA. pp. 14–26. ISBN 978-0-88385-569-0
- ↑ Eves dates Leibniz's first use to the year 1694 and also similarly relates the usage to "as a term to denote any quantity connected with a curve, such as the coordinates of a point on the curve, the slope of the curve, and so on" (Predefinição:Harvnb).
- ↑ "...although we do not find in [the mathematicians of Ancient Greece] the idea of functional dependence distinguished in explicit form as a comparatively independent object of study, nevertheless one cannot help noticing the large stock of functional correspondences they studied." (Predefinição:Harvnb)
- ↑ N. Bourbaki (18 de setembro de 2003). Elements of Mathematics Functions of a Real Variable: Elementary Theory. [S.l.]: Springer Science & Business Media. pp. 154–. ISBN 978-3-540-65340-0
- ↑ "On the vanishing of trigonometric series," 1834 (Predefinição:Harvnb).
- ↑ Über die Darstellung ganz willkürlicher Funktionen durch Sinus- und Cosinusreihen," 1837 (Predefinição:Harvnb).
- ↑ "By a mapping φ of a set S we understand a law that assigns to each element s of S a uniquely determined object called the image of s, denoted as φ(s). Predefinição:Harvnb
Bibliografia
- Ávila, Geraldo Severo de Souza. (2005). Análise matemática para licenciatura. São Paulo. Edgard Blücher. ISBN 85-212-0371-3.
- Barboni, Ayrton; Paulette, Walter. (2007). Fundamentos de Matemática: Cálculo e Análise. Editora LTC. ISBN 978-85-216-1546-0.
- Iezzi, G; Murakami, C.. (2013). Fundamentos de Matemática Elementar: Conjuntos e Funções. vol. 1, 9. ed., Atual Editora:São Paulo. ISBN 9788535716801.















































































































 " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">


