Fração

Predefinição:PU-AO45 é um modo de expressar uma quantidade a partir de uma razão de dois números inteiros. A palavra fração vem do latim fractus e significa "partido", dividido ou quebrado (do verbo frangere: "quebrar").

Representação gráfica de fração. Observa-se facilmente a equivalência entre 2/4 e 1/2.

Surgimento e sua Precisão

No antigo Egito por volta do ano 3000 a.C., o faraó Sesóstris distribuiu algumas terras às margens do Rio Nilo para alguns agricultores privilegiados. O privilégio em possuir essas terras era porque todo ano, no mês de julho, as águas do rio inundavam essa região ao longo de suas margens e fertilizavam os campos. Essas terras, portanto, eram bastante valorizadas.

Porém, era necessário remarcar os terrenos de cada agricultor em setembro, quando as águas baixavam. Os responsáveis por essa marcação eram os agrimensores, que também eram chamados de estiradores de corda, pois mediam os terrenos com cordas nas quais uma unidade de medida estava marcada.

Essas cordas eram esticadas e se verificava quantas vezes a tal unidade de medida cabia no terreno, mas nem sempre essa medida cabia inteira nos lados do terreno. Esse problema só foi resolvido quando os egípcios criaram um novo número: o número fracionário. Ele era representado com o uso de frações, porém os egípcios só entendiam a fração como uma unidade (ou seja, frações cujo numerador é igual a 1).

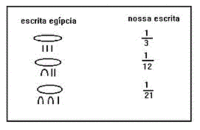
Eles escreviam essas frações com uma espécie de sinal oval escrito em cima do denominador. Mas os cálculos eram complicados, pois no sistema de numeração que usavam no antigo Egito os símbolos se repetiam muitas vezes.

Só ficou mais fácil trabalhar com as frações quando os hindus criaram o Sistema de numeração decimal, quando elas passaram a ser representadas pela razão de dois números naturais.

Desde então, as frações foram usadas para a resolução de diversos tipos de problemas matemáticos. Uma das formas mais correntes de se trabalhar com frações é a porcentagem, em que se expressa uma proporção ou uma relação a partir de uma fração cujo denominador é 100. O uso de frações também é de valia extrema para a resolução de problemas que envolvem regra de três.

Definições

De modo simples, pode-se dizer que uma fração de um número, representada de modo genérico como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a}{b},} designa o inteiro dividido em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {b}} partes iguais ao qual usa-se o número Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {a}} de partes. Neste caso, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {a}} corresponde ao numerador, enquanto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {b}} corresponde ao denominador.

O denominador corresponde ao número de partes que um todo será dividido e o numerador corresponde ao número de partes que serão consideradas.

Ex.: Uma professora tem que dividir três folhas de papel de seda entre quatro alunos, como ela pode fazer isso?

Cada aluno ficara com 3:4 = Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{3}{4}} (lê-se três quartos) da folha. Ou seja, você vai dividir cada folha em 4 partes e distribuir 3 para cada aluno.

Por exemplo, a fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{56}{8}} (lê-se cinquenta e seis oitavos) designa o quociente de 56 por 8. Ela é igual a 7, pois 7 × 8 = 56. A divisão é a operação inversa da multiplicação.

Os números expressos em frações são chamados de números racionais, cujo conjunto é representado por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb Q.} Assim, o conjunto dos números racionais podem ser escritos na forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac {a}{b},} sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a,b \in \mathbb{Z}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \neq 0,} o que resulta em: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{Q}=\left\{\begin{matrix}\frac{a}{b}\end{matrix}\,|\,a\in\mathbb{Z}\,;\,b\in\mathbb{Z^{*}}\right\}.}

Outro modo de enxergar frações é imaginar uma linha reta entre os números 0 e 1. As frações serão pontos nessa reta. Por exemplo, a fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}} é representada por um ponto exatamente na metade dessa reta.

É possível efetuar operações básicas com as frações: adição, subtração, multiplicação, divisão, potenciação, radiciação.

Nomenclatura (leitura) de frações

Regras para leitura dos denominadores.

A leitura de uma fração depende do seu denominador, podendo ser dividida em dois grupos.

O primeiro grupo compreende os denominadores iguais a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 7} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 8} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 9} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1000} .

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle *} Lê-se primeiro o numerador seguido de seu denominador.

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{2}\Rightarrow} três metades; Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\qquad\frac{2}{6}\Rightarrow} dois sextos; Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\qquad\frac{1}{10}\Rightarrow} um décimo;

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}\Rightarrow} um terço;Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\qquad\quad\frac{4}{7}\Rightarrow} quatro sétimos; Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\frac{8}{100}\Rightarrow} oito centésimos;

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{4}\Rightarrow} cinco quartos; Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\quad\frac{6}{8}\Rightarrow} seis oitavos;Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\qquad\frac{2}{1000}\Rightarrow} dois milésimos;

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{5}\Rightarrow} sete Quintos;Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\qquad\frac{3}{9}\Rightarrow} três nonos;Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\qquad\frac{1}{1}\Rightarrow} um inteiro

O segundo grupo compreende os denominadores que não pertencem ao primeiro, e acrescentamos a palavra AVOS

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{15}\Rightarrow} sete quinze avos;

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{13}{57}\Rightarrow} treze cinquenta e sete avos;

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{45}{182}\Rightarrow} quarenta e cinco cento e oitenta e dois avos;

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{21}\Rightarrow} sete vinte e um avos.

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{11}{0}\Rightarrow} onze zero avos.

Tipos de Frações

Frações Equivalentes

Duas ou mais frações que representam a mesma porção da unidade. É obtida quando multiplicamos ou dividimos o numerador e denominador de uma fração por um mesmo número, diferente de zero.

Exemplo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}\cdot \frac{2}{2}=\frac{2}{6}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}\cdot \frac{3}{3}= \frac{3}{9}}

A partir da definição temos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{3}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{2}{6}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{3}{9}} são Equivalentes.

Podemos verificar se duas frações são equivalentes multiplicando os números de forma cruzada.

Exemplo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{9}=\frac{6}{18}\Longrightarrow 3\cdot18=9\cdot6\Longrightarrow 54=54}

O conjunto de frações equivalentes a uma certa fração chama-se Classe de Equivalência.

Frações Irredutíveis e Simplificação de Frações

Para simplificar uma fração, devemos dividir sucessivamente o numerador e o denominador por um divisor comum, até obtermos a fração com os menores termos possíveis. Outra forma de simplificação é pelo MDC(Máximo Divisor Comum), onde efetuamos uma única divisão.

A fração, cujo numerador e denominador são primos entre si, é denominada fração irredutível ou forma simplificada, pois não são possíveis novas simplificações.

Exemplo 1

Para simplificar a fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{14}{30},} basta observar que tanto o numerador quanto o denominador são divisíveis por dois. Neste caso, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{14}{30} = \frac{14}{30} \times 1 = \frac{14}{30} \times \frac{1/2}{1/2} = \frac{14 / 2}{30 / 2} = \frac{7}{15}.}

A simplificação desta fração requer apenas a divisão, haja vista que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle mdc(7,15)=1,} isto é, não podemos simplificar mais os números que não têm divisores em comum.

Exemplo 2

Considerando que o numerador e o denominador de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{78}{12}} são divisíveis por 2 e por 3, obtém-se: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{78}{12} = \frac{78}{12} \times 1 = \frac{78}{12} \times \frac{1/2}{1/2} = \frac{78 / 2}{12 / 2} = \frac{39}{6} = \frac{39}{6} \times 1 = \frac{39}{6} \times \frac{1/3}{1/3} = \frac{39 / 3}{6 / 3} = \frac{13}{2}.}

Neste caso, a obtenção da forma irredutível concretizou-se após duas divisões.

Exemplo 3

Simplificando sucessivamente, tem-se: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{18}{54} = \frac{18/2}{54/2} = \frac{9}{27} = \frac{9/3}{27/3} = \frac{3}{9} = \frac{3/3}{9/3} = \frac{1}{3}.} Alternativamente, dividindo uma única vez pelo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle mdc(18,54)=18:} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{18}{54} = \frac{18/18}{54/18} = \frac{1}{3}.}

Observe que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} é uma fração irredutível equivalente a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{18}{54}.}

Frações Próprias

É a fração, onde o numerador é menor que o denominador e que representa parte do inteiro, isto é, representa um valor maior que zero e menor que um.

Exemplos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}\cdots}

Frações Impróprias

A fração que não é própria é denominada imprópria,o seu numerador é maior ou igual ao denominador.^[2] e representam valores maiores que 1 ou o zero ou o inteiro.

Exemplos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{3}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{2}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{2} \cdots}

Frações Aparentes

É a fração onde o numerador é múltiplo do denominador, elas representam um número inteiro, mas em forma de fração. Frações aparentes são particularidades das frações impróprias.

Exemplos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{25}{5}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{18}{3}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{14}{7} \cdots}

Frações Mistas

É a fração constituída por uma parte inteira e uma fracionária.^[6] Pode-se encontrar uma fração imprópria a partir do número misto.

Exemplos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4\frac{2}{3}} que é equivalente a fração imprópria Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{14}{3}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad \qquad 3\frac{2}{8}} que é equivalente a fração imprópria Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{26}{8}} .

Conversão de Frações Mistas e Impróprias

Para escrever uma fração de forma Imprópria em uma fração de forma Mista, inicialmente devemos dividir o numerador pelo seu denominador. Tomamos como exemplo a fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{9}{4}} :

Com isso o quociente da divisão é a parte inteira da fração mista, o resto será seu numerador e o divisor será seu denominador.

Então temos:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\frac{1}{4}} equivale a fração imprópria Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{9}{4}} .

Outro de modo:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{9}{4}=\underbrace{ \frac{4}{4}+\frac{4}{4} }_{2}+\underbrace{\frac{1}{4}}_{\frac{1}{4}}\Rightarrow 2\frac{1}{4}}

Para transformar uma fração mista em uma fração imprópria, devemos fazer a soma da parte inteira com a parte fracionária da fração mista.

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\frac{1}{4}= 2+\frac{1}{4}=\frac{8}{4}+\frac{1}{4}= \frac{8+1}{4} = \frac{9}{4}} .

Frações Compostas

São frações onde o numerador, o denominador ou ambos possuem frações, também são conhecidas por Frações Complexas.

Exemplo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\frac{2}{7}\over \frac{5}{9}}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\frac{17}{11}+\frac{3}{14}\over \frac{6}{11}\cdot\frac{1}{3}}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\frac{2}{3}\over 5}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {11 \over \frac{7}{16}+\frac{1}{2}} \cdots}

Frações Unitárias

É a fração onde o numerador é igual a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} e o denominador é um inteiro positivo. Exemplo:Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{5}}

A soma das frações unitárias, distintas entre si é chamada de Fração Egípcia, pois para os egípcios era mais prático e fácil de comparar as quantidades dessa forma. Exemplo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3} + \frac{1}{15} = \frac{2}{5}} .

Para explicar os métodos egípcios nas decomposições de uma fração em uma soma de frações unitárias, usaremos duas afirmações:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i)} Toda fração da forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{n}} pode ser decomposta como:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{n+k} +} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\frac{1}{\frac{n(n+k)}{k}}}} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in\mathbb{N}^*} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} variando de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{n+k} + \frac{1}{n(n+k)}\cdot\frac{k}{1} = \frac{1}{n+k}+\frac{k}{n(n+k)} = \frac{n}{n(n+k)}+\frac{k}{n(n+k)}=\frac{n+k}{n(n+k)}=\frac{1}{n}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ii)} Dada a fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{w}} , podemos transformar o denominador Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w} em um produto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} .

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{p\cdot q}= \frac{1}{p\cdot r}+\frac{1}{q\cdot r}} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\frac{p+q}{z}} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z \in \mathbb{R}^*}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{p\cdot q} = } Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\frac{1}{\frac{p\cdot(p+q)}{z}}} + {\frac{1}{\frac{q\cdot(p+q)}{z}}} }

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{p\cdot q} = \frac{1}{1}\cdot\frac{z}{p\cdot(p+q)} + \frac{1}{1}\cdot\frac{z}{q\cdot(p+q)}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{p\cdot q}=\frac{z}{p\cdot(p+q)}+\frac{z}{q\cdot(p+q)}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{p\cdot q}=\frac{z\cdot q +z\cdot p}{p\cdot q\cdot(p+q)}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{p\cdot q}=\frac{z\cdot(p+q)}{p\cdot q\cdot(p+q)}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{z}{p\cdot q}=\frac{z}{p\cdot q}}

Fração Contínua

Também conhecida como Fração Continuada, é uma forma de representar números reais. A fração contínua de um número racional pode ser representada por uma sequência finita de inteiros, já a de um número irracional é representada por uma sequência infinita de inteiros.

Para obter uma fração continua, podemos aplicar o algoritmo da divisão de Euclides sucessivamente em uma divisão de inteiros. Usando um racional irredutível, temos que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{t}{s}} tal que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=a_1\cdot s+r_1} , com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0< r_1<s}

Logo, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{t}{s}=\frac{a_1\cdot s}{s}+ \frac{r_1}{s}= a_1 + \frac{1}{\frac{s}{r_1}} } ,

Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_1} , obtemos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_2} tal que, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=a_2\cdot r_1+r_2} , com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0< r_2<r_1}

Logo, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{t}{s}=a_1+\frac{1}{a_2+\frac{r_1}{r_2}}}

E assim sucessivamente, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{t}{s}= a_1+\frac{1}{a_2+\frac{1}{a_3 +\frac{1}{\cdots a_{n-1}+\frac{1}{a_n}}}}} , com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \in \mathbb{N^*}}

Como o algoritmo da divisão de Euclides é um processo finito, escrevemos essa fração contínua que representa o racional Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{t}{s}} dessa maneira:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{t}{s}= [a_1,a_2,a_3,\cdots,a_n]} .

Fração Decimal

Toda fração cujo denominador é uma potência positiva de 10 é chamada de fração decimal. Essas frações podem ser representadas por um número decimal.

Exemplos: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{10}=0,2} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-11}{100}=} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-11}{10^2}=-0,11} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{1000}=} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{10^3}=0,007\cdots}

Teorema: A parte fracionária de cada fração decimal(positiva) pode ser decomposta como uma soma de frações decimais especiais, e cada uma delas tem como numerador um dos dígitos que expressa o denominador da fração original.

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{584}{1000}=\frac{5}{10}+\frac{8}{100}+\frac{4}{1000}=0,584}

Podemos verificar que todo número racional determinado por uma fração decimal terá quantidade finita de dígitos na parte fracionária, ou seja tem expansão finita.

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \{^+_- a_n a_{n1} \cdots a_1 a_0,b_1 b_2\cdots b_n\}} .

Fração Ordinária

É toda fração da forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a}{b}} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} é um inteiro qualquer e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} um inteiro estritamente positivo.

Exemplo: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-2}{3}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}\cdots}

Teorema: Quando o denominador de uma fração ordinária tiver uma fatoração em primos,

contendo apenas os fatores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2} e/ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5} , esta fração será equivalente a uma fração decimal.

Demonstração: Sendo a fração Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a}{b}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \quad a} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \in \mathbb{Z}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b\neq0} .

Pela Hipótese Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=2^{m}\cdot 5^{n}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \quad m} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \in \mathbb{Z}} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \quad m} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\geq0} .

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow m>n}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a}{b}=\frac{a}{2^{m}\cdot 5^{n}} \cdot \frac{5^{m-n}}{5^{m-n}}= \frac{a\cdot 5^{m-n}}{2^{m}\cdot 5^{n+m-n}}=\frac{a\cdot 5^{m-n}}{(2\cdot5)^{m}}=\frac{a\cdot 5^{m-n}}{10^m}}

Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m<n} a demonstração é de forma análoga.

Proposição: Todo numero racional Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} , tem uma decomposição na forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=r'+r''} , onde:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r'\geq 0} e é um número inteiro (parte inteira de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} )

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r''} é um racional, sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\leq r''\leq 1} (parte fracionária de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} )

Com isso temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dec(r)=dec(r')+dec(r'')} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dec=} decimal

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\frac{8}{5}=\underbrace{ 1,6=1+0,6 }_{r=r'+r''}}

Temos ainda:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle *} A parte inteira Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r'} de $r$ pode ser obtida como o quociente $q$, da divisão euclidiana de $a$ por $b$, onde $a$, $b>0$ e é uma representação em fração ordinária de $r$, ou seja $r={\frac {a}{b}}$ .

Pela divisão euclidiana $a=b\cdot q+s$, então $8=5\cdot 1+3$, onde $1=q=r'$

$*$ A parte fracionária $r''$ de $r$ é $r-q$, ou seja

$\underbrace {r-r'=r''} _{1,6-1=0,6}$ ou $r-q=r''$

Ou seja, $r''={\frac {b_{1}}{10}}+{\frac {b_{2}}{10^{2}}}+{\frac {b_{3}}{10^{3}}}+\cdots +{\frac {b_{n}}{10^{n}}}$.

Comparação entre frações

Comparar frações significa analisar qual representa a maior ou menor quantidade ou ainda, se elas são iguais(equivalentes).

Para comparar as frações temos duas situações:

$1^{\circ })$ As frações possuem denominadores iguais:

Para analisar as frações com mesmo denominador, basta verificar seu numerador.

Exemplo: Temos as seguinte frações ${\frac {1}{3}}$ e ${\frac {2}{3}}$, como $2$ é maior que $1$, então ${\frac {2}{3}}>{\frac {1}{3}}$.

$2^{\circ })$ As frações possuem denominadores diferentes:

Para compararmos frações com denominadores diferentes precisamos reduzi-las a um mesmo denominador. Podemos fazer de dois modos:

$a)$ Pelo MMC:

Dadas as seguintes frações: ${\frac {2}{5}}$ e ${\frac {2}{3}}$. faremos o $mmc$ entre os dois denominadores e ao obter o resultado transformaremos em novas frações equivalentes a primeira e com denominadores iguais.

Temos então: ${\begin{array}{c|}3&5\\\hline 1&5\\&1\\\end{array}}{\begin{array}{lcl}3\\5\end{array}}$ $\quad 3\cdot 5=15$

Como $3$ e $5$ são números primos o $mmc(3,5)=15$, este resultado será o denominador comum entre as frações.

Para obtermos o novo numerador, dividimos o número $15$ pelo denominador da primeira fração, e o resultado multiplicamos com o numerador. Então:

Pegando a fração ${\frac {2}{5}}$,

${\begin{aligned}15\div 5&=3\\&\Rightarrow 3\cdot 2=6\\\end{aligned}}$

$\Longrightarrow {\frac {6}{15}}$

Fazemos o mesmo com a fração ${\frac {2}{3}}$,

${\begin{aligned}15\div 3&=5\\&\Rightarrow 5\cdot 2=10\\\end{aligned}}$

$\Longrightarrow {\frac {10}{15}}$

Uma vez igualados os denominadores, pode-se fazer a comparação entre as frações:

$\qquad \qquad {\frac {2}{5}}<{\frac {2}{3}}\qquad \qquad \qquad$

pois $\qquad {\frac {6}{15}}<{\frac {10}{15}}$.

$b)$Multiplicando Cruzado:

Neste caso multiplicamos o numerador da primeira fração com o denominador da segunda e o numerador da segunda fração pelo denominador da primeira.

${\frac {a}{b}}\times {\frac {c}{d}}\Longrightarrow a\cdot d\quad {\text{e}}\quad c\cdot b$

Com isso, temos:

$\Rrightarrow {\frac {a}{b}}>{\frac {c}{d}}$ quando $a\cdot d>c\cdot b$ e

$\Rrightarrow {\frac {c}{d}}>{\frac {a}{b}}$ quando $c\cdot b>a\cdot d$

Caso o resultado seja igual $a\cdot d=c\cdot b$ significa que elas são equivalentes.

Exemplo: ${\frac {4}{5}}{\text{ }}{\text{e}}{\text{ }}{\frac {1}{3}}$

$\Rightarrow {\frac {4}{5}}\times {\frac {1}{3}}$

$\Rightarrow 4\cdot 3=12\quad {\text{e}}\quad 1\cdot 5=5$

Temos então, $12>5$, logo

$\qquad \qquad \quad {\frac {4}{5}}>{\frac {1}{3}}$.

Adição e Subtração de Frações

Assim como na comparação de frações, na adição e subtração temos dois casos:

$\vartriangleright$ Com denominadores iguais;

$\vartriangleright$ Com denominadores diferentes.

$1^{\circ })$ Frações com o mesmo denominador:

Para frações com denominador em comum, somamos ou subtraímos os numeradores de acordo com a operação solicitada e mantemos o denominador.

Exemplos:

$\qquad \qquad a)$ ${\frac {2}{9}}+{\frac {5}{9}}={\frac {2+5}{9}}={\frac {7}{9}}$

$\qquad \qquad b)$ ${\frac {5}{3}}-{\frac {1}{3}}={\frac {5-1}{3}}={\frac {4}{3}}$

Essa expressão pode ser escrita também deste modo:

$\quad 1{\frac {2}{3}}-{\frac {1}{3}}=1{\frac {2-1}{3}}=1{\frac {1}{3}}$

$*$ no caso de ter duas frações mistas, somamos ou subtraímos os números inteiros, mantemos o denominador e somamos ou subtraímos o numerador.

$2^{\circ })$ Frações com denominadores diferentes:

Neste caso temos que transformar as frações em uma fração com denominador em comum, fazemos isso através do MMC.

Por exemplo: ${\frac {1}{9}}+{\frac {3}{6}}$

Fazendo o $mmc$ entre os denominadores, teremos: ${\begin{array}{c|}9&6\\\hline 9&3\\3&1\\1&\end{array}}{\begin{array}{lcl}2\\3\\3\end{array}}$$\qquad 2\cdot 3\cdot 3=18$

O $mmc(9,6)=18$.

Agora que encontramos um denominador em comum, faremos o processo análogo ao processo de comparação entre frações com denominadores diferentes, porém iremos somar seus numeradores, mantendo o denominador que tivemos como resultado do $mmc$. Temos então:

${\frac {1}{9}}+{\frac {3}{6}}={\frac {1\times 2}{18}}+{\frac {3\times 3}{18}}={\frac {2}{18}}+{\frac {9}{18}}={\frac {11}{18}}$

Na subtração o processo é análogo.

Multiplicação de Frações

Tendo as seguintes frações ${\frac {a}{b}}$ e ${\frac {c}{d}}$, para multiplica-las basta fazer o produto de seus numeradores e o produto de seus denominadores, temos então:

${\frac {a}{b}}\times {\frac {c}{d}}={\frac {a\cdot c}{b\cdot d}}$, com $a$, $b$, $c$ e $d\in \mathbb {R}$

Exemplo: ${\frac {2}{3}}\times {\frac {1}{3}}={\frac {2\cdot 1}{3\cdot 3}}={\frac {2}{9}}$

No caso de um número inteiro multiplicar uma fração, fazemos o produto do número inteiro com o numerador e conservamos o denominador, isso ocorre porque o número inteiro na fração possui como denominador o número $1$, e qualquer número multiplicado por $1$ é ele mesmo.

Exemplo: $1\times {\frac {2}{3}}={\frac {1\cdot 2}{3}}={\frac {2}{3}}$

É o mesmo que fazer ${\frac {1}{1}}\times {\frac {2}{3}}={\frac {1\cdot 2}{1\cdot 3}}={\frac {2}{3}}$

Divisão

Para efetuar a divisão entre duas frações, multiplica-se a fração que está no numerador pelo inverso da fração que está no denominador. Ex.:${\frac {\frac {3}{4}}{\frac {5}{2}}}={\frac {3}{4}}\times {\frac {2}{5}}={\frac {6}{20}}={\frac {3}{10}}.$

No último passo foi feita Simplificação de Frações.

Exponenciação ou potenciação de frações

É indiferente resolver primeiro a exponenciação ou a divisão:

$$\left({\dfrac {1}{2}}\right)^{2}={\dfrac {1^{2}}{2^{2}}}={\dfrac {1}{4}}=0,25$$

Efetuando-se primeiramente a divisão obtém-se o mesmo resultado:

$$\left({\dfrac {1}{2}}\right)^{2}=({0,5})^{2}=0,25$$

Radiciação

A raiz de uma fração é feita seguindo-se os mesmos passos da potenciação:

${\sqrt {\frac {1}{4}}}={\frac {\sqrt {1}}{\sqrt {4}}}={\frac {1}{2}}=0,5$

E, analogamente, é possível fazer a divisão antes da radiciação.

Expoente fracionário

Da mesma forma que na divisão entre frações, a ocorrência de expoente fracionário causa a inversão da operação:

$$8^{{2} \over {3}}={\sqrt[{3}]{8^{2}}}={\sqrt[{3}]{64}}={4}$$

Corpo de frações

Ver artigo principal: Corpo de frações

Se um conjunto $A$ tem duas operações binárias $+$ e $\times$ satisfazendo determinadas propriedades, pode-se perguntar em que condições é possível estender $A$ para um outro conjunto $B$ com operações binárias $+$ e $\times$, de forma que $(B,+,\times )$ seja um corpo e as operações $A+B$ e $A\times B$ dêem o mesmo resultado quando efetuadas em $A$ ou em $B$. Quando possível, temos a construção do corpo de frações.