Projeção gnomônica

Esquema de uma projecção azimutal gnomónica

Projeção Central ou Gnomônica é a projeção de uma esfera sobre um plano tangente a partir do seu centro.

A projeção de gnomônica (ou projeção plana gnomônica) utiliza como superfície de projeção um plano tangente à superfície da Terra, no qual os pontos são projetados geometricamente, a partir do centro da Terra. Esta é, provavelmente, a mais antiga das projeções, acreditando-se que foi desenvolvida por Tales de Mileto, cerca de 600 a.C.

Projecção gnomónica centrada no ponto 0ºN, 0ºE.

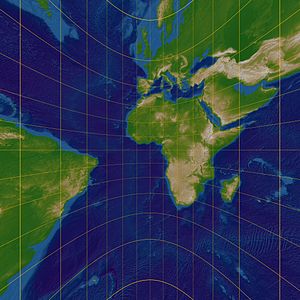
A projeção gnomônica apresenta todos os tipos de deformações. A projeção não é equidistante; a escala só se mantém exata no ponto de tangência, variando rapidamente à medida que se afasta desse ponto. Além disso, a projeção não é conforme, nem equivalente. As distorções são tão grandes que as formas, as distâncias e as áreas são muito mal representadas, exceto nas proximidades do ponto de tangência.

A propriedade notável desta projeção é que as geodésicas (que, na esfera, são os círculos máximos) são representadas como linhas retas. Os meridianos aparecem como retas convergindo para o pólo mais próximo. Os paralelos, exceto o equador (que é um círculo máximo) aparecem como linhas curvas. Além disso, na projeção gnomônica, como em todas as projeções azimutais, os azimutes a partir do ponto de tangência são representados sem deformações.

Em Cartografia Náutica, a projeção gnomônica é empregada principalmente na construção de Cartas para Navegação Ortodrômica. Sendo também aplicada em radiogoniometria com estação fixa, aproveitando-se a propriedade da projeção gnomônica de representar sem deformações os azimutes (marcações) tomados a partir do ponto de tangência (que, neste caso, será a posição da estação radiogoniométrica). Por outro lado, sabe-se que não é possível representar as regiões polares na Projeção de Mercator, devido à sua impossibilidade material da representar o pólo e por causa das deformações excessivas apresentadas em Latitudes muito altas. Esta importante lacuna pode ser preenchida pela projeção gnomônica.

Veja também

• Gnômon

Ligações externas

• Weisstein, Eric W. "Gnomonic Projection." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/GnomonicProjection.html