Toro (topologia)

Toro
Notação	$\mathbb {T} ^{2}$
Característica de Euler	0
Grupo fundamental	$\mathbb {Z} \times \mathbb {Z}$
Homologia	$\mathbb {Z} \times \mathbb {Z}$

Animação Toróide

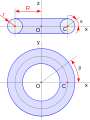
Toro ou toróide é um espaço topológico homeomorfo ao produto de dois círculos. Apresenta o formato aproximado de uma câmara de pneu. Em geometria, pode ser definido como o lugar geométrico tridimensional formado pela rotação de uma superfície circular plana de raio r, em torno de uma circunferência de raio R.

Formas de construir um toro

• Identificando os lados opostos de um quadrado sem os torcer.
• Identificando os lados opostos de um hexágono sem os torcer.

Geometria

Um toro pode ser imerso no $\mathbb {R} ^{3}\,$ como uma superfície algébrica do quarto grau.

Em coordenadas paramétricas, o toro é gerado por:

$x(u,v)=(R+r\cos {v})\cos {u}\,$

$y(u,v)=(R+r\cos {v})\sin {u}\,$

$z(u,v)=r\sin {v}\,$

em que

u, v estão no intervalo [0, 2π],

R é a distância do centro do tubo ao centro do toro,

r é o raio do tubo.

Em coordenadas cartesianas, o toro com simetria de rotação no eixo z tem equação:

$\left(R-{\sqrt {x^{2}+y^{2}}}\right)^{2}+z^{2}=r^{2},\,\!$

eliminando a raiz quadrada, chega-se a:

$(x^{2}+y^{2}+z^{2}+R^{2}-r^{2})^{2}=4R^{2}(x^{2}+y^{2}).\,\!$

A área da superfície e o volume do interior são dados por:

$A=4\pi ^{2}Rr=\left(2\pi r\right)\left(2\pi R\right)\,$

$V=2\pi ^{2}Rr^{2}=\left(\pi r^{2}\right)\left(2\pi R\right).\,$

As fórmulas da área e do volume são as mesmas de um cilindro, em que sua altura é o equivalente à circunferência média do toro $(2\pi R)$ e o raio da base equivalente ao raio da seção transversal do toro $(r)$. Este cilindro é criado "cortando-se" o toro e estendendo-o pelo centro do tubo. As perdas em área e volume na parte interna são compensadas por ganhos na parte externa.

Propriedades topológicas

O toro é uma superfície topológica compacta, conexa e orientável, que pode ser representada por um polígono (no caso, quadrado) com uma orientação nas arestas. Esta orientação representa a identificação das arestas. Uma possível triangulação do toro é dada pela figura abaixo, na qual o toro é representado pelo quadrado com os lados identificados .

Triangulação do Toro

Podemos também triangularizar o bitoro, que é uma soma conexa de dois toros, triangularizando a região poligonal que o representa, que é um polígono com uma orientação nas arestas. Esta orientação determina como as arestas devem ser coladas para formar a figura topológica. Uma possível triangulação do bitoro é dada pela figura abaixo:

Bitoro

Triangulação do Bitoro

Ver também

• Esfera
• Superfície

Bibliografia

• Kozak, Ana Maria; Pompeya Pastorelli Sonia, Verdanega Pedro Emilio (2007). Nociones de Geometria Analitica y Algebra Lineal (em espanhol). [S.l.]: Mcgraw-Hill. 744 páginas. ISBN 9789701065969  !CS1 manut: Língua não reconhecida (link)
• Hatcher, Allen (2002). Algebraic Topology (em inglês). [S.l.]: Cambridge University Press. ISBN ISBN 0-521-79540-0  !CS1 manut: Língua não reconhecida (link)
• Nikulin, V.V; I.R.Shafarevich (1987). Geometries and Groups (em inglês). [S.l.]: Springer. ISBN 9783540152811  !CS1 manut: Língua não reconhecida (link)
• Munkres, J. (1966). Elementary Differential Topology, edição revisada. Col: Annals of Mathematics Studies 54. [S.l.]: Princeton University Press. ISBN 0-691-09093-9 
• "Tore (notion géométrique)" at Encyclopédie des Formes Mathématiques Remarquables

Ligações externas

• Creation of a torusem Cut-the-Knot
• "4D torus"Fly-through cross-sections of a four dimensional torus.
• "Relational Perspective Map"Visualizing high dimensional data with flat torus.
• "Torus Games"Free downloadable games for Windows and Mac OS X that highlight the topology of a torus.
• Polydos
• Hatcher, 2002

Galeria

• 
• 

  Superfície tórica

• 

  Caixa d'água toroidal na Polônia

•