𝖂𝖎ƙ𝖎𝖊

Perspectiva (gráfica)

Disambig grey.svg Nota: Se procura outros usos da palavra Perspectiva, veja Perspectiva.
Construção geométrica de uma perspectiva que mescla os processos com um e dois pontos de fuga.[1] Gravura de Henricus Hondius.
Diferentes sistemas de perspectiva.

A palavra perspectiva significa ver através de, um dos significados de perspicere, em uma tradução literal da palavra grega optiké.[2]

Ainda Erwin Panofsky e outros teóricos[3] levantam a hipótese de que o termo possa ser uma tradução da palavra italiana prospettiva.[2]

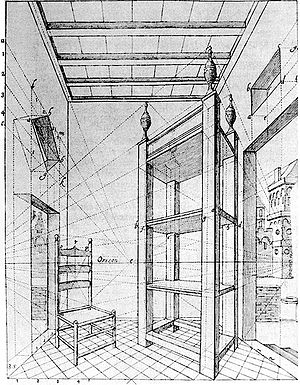
A interpretação de Dürer se baseia na definição moderna que entende a perspectiva como uma seção transversal provocada na pirâmide visual (ou cone visual, que deu origem ao termo perspectiva cônica), pelo plano do quadro.[4]

Desde o seu surgimento, na Renascença, quase toda pintura obedecia a esse método de representação. A perspectiva era um expediente geométrico que produzia a ilusão da realidade, mostrando os objetos no espaço em suas posições e tamanhos corretos. A perspectiva capta os fatos visuais e os estabiliza, transformando o observador em aquele para o qual o mundo todo converge.[5]

História

No sentido lato, se a perspectiva é "a ciência da representação dos objetos numa superfície, da forma como surgem ao olhar humano, vistos de uma certa distância", seria descabido não reconhecer que, neste contexto, a perspectiva já existia na antiguidade.[6]

Na antiguidade egípcia, muito antes do surgimento dos processos de perspectiva com pontos de fuga, as pinturas e desenhos normalmente utilizavam uma escala para objetos e personagens de acordo com seu valor espiritual ou temático; por exemplo, o faraó fatalmente era representado em tamanho maior que o de seus súditos. Iconograficamente a tradição impunha que os elementos retratados tomassem a forma mais fácil de reconhecimento, o que terminava por fragmentar os "modelos" a partir de pontos de vista "frontais" (lei da frontalidade).[7]

Os gregos, depois de terem seus desenhos fortemente influenciados pela lei da frontalidade, partiram para o naturalismo e quase descobriram as leis da perspectiva geométrica, mas uma experiência malsucedida os afastou dessa ideia, pois os corpos mais distantes se projetaram maiores no plano de projeção, quando na realidade o que está mais distante deve parecer menor.[7]

Ilustração da tradução em Francês antigo da Histoire d'Outremer de Guillaume de Tyr, entre 1200 e1300. As arestas paralelas dos objetos, ao se distanciarem do observador, fixo, deveriam convergir para um ponto (ponto de fuga), porém, elas não o fazem.

Durante o período medieval alguns estilos abandonaram por completo qualquer intenção de se alcançar uma ilusão visual de profundidade.[8] No entanto, a influência dos esforços gregos (e romanos, em evolução à arte grega) permaneceu viva e os artistas pré-perspectivistas usaram as linhas diagonais como formas de obtenção de espaço, embora não tenham se dado conta da existência do ponto de fuga. Esse tipo de processo empírico ficou conhecido como perspectiva espinha de peixe.[9]

A base óptica da perspectiva pode ter sido definida no ano 1000, quando o matemático e filósofo árabe Alhazen,[10] na sua obra Perspectiva, pela primeira vez demonstrou que a luz projeta-se em formato cônico no olho humano. Isto era, teoricamente, suficiente para traduzir objetos de modo convincente em uma pintura, mas Alhalzen estava preocupado apenas com a óptica, não com métodos de representação. Traduções cônicas são matematicamente difíceis, de forma que a construção de um desenho utilizando-se delas seria bastante demorado.

Giotto foi um dos primeiros artistas italianos, já em um contexto que se aproximava do Renascimento naquele país, a utilizar-se de métodos algébricos para determinar a distância entre linhas. No entanto, tal método possuía deficiências e não retratava fielmente uma sequência de linhas em um determinado campo visual. Uma das primeiras obras de Giotto, na qual ele se utiliza dessa técnica, foi Jesus ante Caifás. Embora esta obra não se encaixe na definição estrita de perspectiva, ela fornece uma ilusão crível de profundidade e pode ser considerada como um passo importante na arte ocidental.[11]

Na era moderna adotou-se o conceito de perspectiva em sua acepção estrita, ou seja, "a ciência da representação de objetos e do espaço que os cerca e da maneira como esses são percebidos pelo olhar, a partir de um ponto de vista fixo".[6]

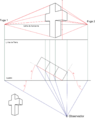
Em meados do século XV, no período da história conhecido como quatrocento, esse "ponto de vista" determinou a perspectiva de projeção central, proposta através de desenhos, por Filippo Brunelleschi (falecido em 1446), a qual chamou de Construzione Legittima e que se baseava num sistema com um ponto de fuga.[12] Brunelleschi percebeu, possivelmente através da pintura da silhueta de diversos edifícios florentinos com o auxílio de um espelho, que todas as linhas daquelas arestas convergiam para um ponto na linha do horizonte. Segundo o biógrafo Vasari, ele então demonstrou a perspectiva por meio de um dispositivo óptico, utilizando-o na sua pintura do Batistério de São João, na Igreja de Santa Maria del Fiore.[13]

O uso da perspectiva na composição deste afresco de Pietro Perugino (localizado na Capela Sistina, 1481–82) ajudou a levar o novo processo a Roma.
Método de Dürer que se utiliza de um vidro quadriculado como plano secante da pirâmide visual.

Décadas depois, Leon Battista Alberti, amigo e admirador de Filippo escreveu o tratado conhecido como Della Pittura (1435) (ou Da pintura em português), no qual explicitavam-se métodos construtivos da perspectiva. Alberti foi considerado por Vasari melhor escritor do que pintor.[14]

Piero della Francesca desenvolveu os estudos apresentados em Della Pittura na sua obra De Prospectiva Pingendi de 1474. Alberti havia limitado a sua obra às figuras posicionadas no plano de terra (ou seja, no "chão"), traçando um panorama da perspectiva geométrica. Francesca foi além, posicionando objetos em praticamente qualquer ponto da ilusão tridimensional da pintura.[15]

Leonardo da Vinci acreditava que a compreensão da perspectiva era fundamental para a pintura e o desenho. Segundo suas anotações, dizia que a prática deve sempre ser construída sobre a teoria, para a qual a perspectiva é o sinal e o portal de entrada, e sem perspectiva nada pode ser feito bem nos campos da pintura.[16]

Fundamentos sólidos da perspectiva matemática foram produzidos por Girard Desargues, no século XVII, ao resgatar a obra de Apolônio e antecipar muitos dos princípios daquela que viria a ser chamada de Geometria projetiva. Desargues, entretanto, não foi reconhecido em sua época por não ter sido considerado "científico" e por não utilizar os princípios da geometria analítica, elemento de credibilidade naquele momento.[17]

Mais tarde, em 1715, os fundamentos matemáticos foram codificados por Brook Taylor, no seu livro intitulado Linear Perspective, os quais propiciaram o surgimento do método exato com dois pontos de fuga.[18]

No início do século XIX os estudos de Desargues foram revisitados por Jean-Victor Poncelet (1788-1867), que elaborou a Geometria projetiva, na sua obra Traité des Propriétés Projectives des Figures, de (1822).[17]

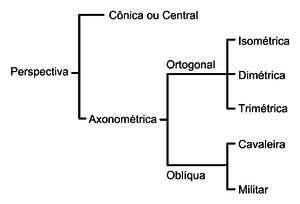
Processos de perspectiva com:

Exemplo do funcionamento de uma projeção que resulta em uma perspectiva (o ponto O indica o observador.)
Exemplo de uma perspectiva isométrica com arcos em formato de semi-isocírculos.
Paralelepípedo em perspectiva dimétrica.
Paralelepípedo em perspectiva trimétrica.
Exemplo de uma perspectiva dimétrica (135º, 135º, 90º), conhecida como cavaleira de 45º (cabinet).
Perspectiva cavaleira "voo de pássaro" ou "olho de pássaro", exemplo de "perspectiva militar".
Variação a 45º da perspectiva militar.

Métodos de representação

Além das representações artísticas, existem três métodos de perspectiva que são muito usados na engenharia, na arquitetura, no desenho industrial e em outras frentes onde a abordagem técnica se faça necessária:[20]

  • Exato (a perspectiva cônica desenhada com os planos de projeção da Geometria descritiva),
  • Axonométrico (subdividido em isométrico, dimétrico e trimétrico) e
  • Oblíquo (em suas diversas variações).

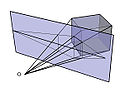
Perspectivas exatas

Ver artigo principal: Perspectiva com um ponto de fuga
Ver artigo principal: Perspectiva com dois pontos de fuga
Ver artigo principal: Perspectiva com três pontos de fuga

Nestes métodos, o objeto é visto num plano secante, o quadro (Q), que intercepta as retas visuais que partem do observado na direção do observador. As perspectivas exatas são projetadas instrumentalmente num plano, a partir de vistas ou das medidas exatas do que será representado. O processo de perspectiva com um ponto de fuga teve origem no final do século XV e foi um dos ícones mais marcantes do Renascimento, a perspectiva com dois pontos de fuga, por sua vez, foi elaborada por Brook Taylor, em 1715, durante o Barroco. Estes processos são mais estudados e utilizados por arquitetos, engenheiros e designers de interiores.[21] Portanto, a ideia básica por trás de qualquer sistema projetivo é a de que existem, três elementos fundamentais para que haja a perspectiva, sendo eles: um observador, um objeto (observado) e um plano de projeção (quadro).

Perspectiva axonométrica

Teórica e diretamente, os métodos paralelos da axonometria, são projeções ortográficas (segundo um observador situado no infinito), que projetam três faces de um cubo em um plano (quadro).[22] A isometria é a situação onde os três eixos (xyz) estão separados por 120 graus. A dimetria dá-se quando tem-se dois ângulos iguais. E a trimetria, por sua vez, ocorre quando as distâncias entre os eixos possuem ângulos distintos; ela também é conhecida como anisometria, pois as medidas das unidades dos três eixos possuem diferentes escalas entre si.

Perspectiva isométrica

Ver artigo principal: Perspectiva isométrica

A perspectiva do tipo isométrica é um caso particular de projeção cilíndrica ortogonal. Ela ocorre, como já dito, quando o observador está situado no infinito (e portanto, as retas projetantes são paralelas entre si) e incidem perpendicularmente ao plano do quadro. O sistema de eixos da situação a ser projetada ocorrerá na perspectiva, se vistos no plano, de forma equi-angular (em ângulos de 120º). Desta forma, é possível traçar uma perspectiva isométrica através de uma malha de retas desenhadas a partir de ângulos de 30º.[23]

O termo "isométrica" vem do grego: "mesma medida", já que as medidas ortogonais, retiradas das vistas ortogonais, são redesenhadas nos eixos x, y e z com os tamanhos indicados pelas cotas. As linhas inclinadas, que estão fora do tri-eixo ortogonal, não têm as mesmas medidas.[24]

Perspectiva dimétrica

O que caracteriza a perspectiva dimétrica é o fato de que dois de seus eixos projetam-se em ângulos iguais no quadro. A escala gráfica de construção é semelhante à da projeção isométrica, mas para ser desenhada são aplicados coeficientes de redução nos eixos horizontais.[25][26]

Ver artigo principal: Perspectiva dimétrica

Perspectiva trimétrica

Na perspectiva trimétrica três ângulos do triedro de referência projetam-se em ângulos desiguais no quadro, desse modo os três eixos devem ser submetidos a coeficientes de redução diferentes.[25][26]

Ver artigo principal: Perspectiva trimétrica

Perspectivas em projeção cilíndrica oblíqua

Cavaleira

Ver artigo principal: Perspectiva cavaleira

As perspectivas paralelas oblíquas (eventualmente chamadas de cavaleiras[27] ou militares) ocorrem quando o observador impróprio (situado no infinito), gera retas projetantes (paralelas) que incidem de forma não-perpendicular no plano do quadro. Desta forma, caso uma das faces do objeto a ser projetado seja paralela ao quadro, esta face estará desenhada em verdadeira grandeza (suas medidas serão exatamente iguais às da realidade) enquanto as demais sofrerão uma distorção perspéctica. O fator de correção (redução) a ser utilizado na mensuração das arestas, depende do ângulo de incidência das projetantes.[28]

Por exemplo, caso as retas projetantes incidam no plano do quadro em ângulos de 45º, as faces a sofrerem distorção terão suas projeções reduzidas à metade do valor real.[28] Objetos com muitos arcos e circunferências na vista frontal são mais fáceis de serem desenhados em cavaleira do que em isométrica.

Voo de pássaro ou militar

Ver artigo principal: Perspectiva militar

Toda perspectiva (cônica ou paralela) que adote o observador muito acima da linha do horizonte, como se estivesse a mirar o chão, é chamada de voo de pássaro. Umas das angulações da cavaleira (com as fugantes a 225 graus), que tem essa característica de sobrevoo, recebe o nome de perspectiva militar.[25] É possível encontrar a militar em processo dimétrico, como se fosse uma perspectiva isométrica em que os ângulos da base são desenhados a 45 graus.[29] Esse processo teve início nos rascunhos feitos pelas patrulhas napoleônicas por meio de balões ou de pontos elevados, na simulação topográfica de terrenos, em mapas destinados às estratégias militares. Após a sua divulgação foi usada por arquitetos alemães na representação de seus planos urbanísticos sob o nome de vogel perspective.[25] Na prática, o plano superior das construções é desenhado no quadro, paralelo ao plano do solo (o quadro é um plano horizontal). Nos ateliês de arquitetura é comum a utilização da perspectiva militar, por ser desenhada a partir da planta, em verdadeira grandeza.

Gravura japonesa.

A perspectiva no oriente

Ao longo da história, o homem sempre procurou utilizar-se dos suportes pictóricos como meio de expressão. Porém, tratou-se de uma questão essencialmente ocidental a busca de uma "reprodução fiel" da visão humana no plano bidimensional: nota-se que na arte do oriente, tal preocupação, ainda que não desapareça, manifesta-se com outras intenções. Nas tradições artísticas não-ocidentais, a perspectiva em sua forma estrita, praticamente inexiste, visto que a visão de mundo e estética daquelas culturas é diferente. Em meados do século XIX, quando ocorre um contato maior entre Ocidente e Oriente, o "diálogo" entre esses extremos criou condições para que a própria visualidade ocidental tenha sofrido uma revolução, quando pintores ligados ao impressionismo, pós-impressionismo e ao art nouveau permitiram-se a influência daquilo que se chamou de japonismo, abrindo caminho para diferentes maneiras de interpretação do espaço.[30] Existem muitos métodos de obtenção espacial em uma imagem, no caso das gravuras orientais, observa-se a utilização da sobreposição, da posição no campo visual (mais para cima, mais longe), da perspectiva atmosférica e das diagonais sem o contexto geométrico da perspectiva.

Cézanne (1890-1894).

Perspectiva estranha

Distorcer a perspectiva ou incluir mais de uma na mesma cena é perturbador, porque o cérebro não encontra as convenções visuais usadas para que as coisas pareçam reais. Pintores como Paul Klee fizeram brincadeiras com os processos existentes.[31]

De Chirico rompeu com as regras para criar uma atmosfera de sonho; na tela Musas inquietantes, de 1925, ele interrompeu um caminho de forma abrupta, desafiando o espectador a olhar na rua além, onde os prédios se parecem se casas de bonecas.[31] Em Mistério e melancolia, de 1914, a perspectiva é tão insólita, que historiadores da segunda metade do século XX, passaram a considerá-lo um pintor surrealista, antes mesmo do início do Surrealismo em 1924.[32]

Cézanne foi o primeiro a fazer experiências com a perspectiva, nas suas sessões de pintura, ao mudar o seu ponto de vista de um lado para o outro.[31] Na pintura Cesta de maçãs, de 1895, a perspectiva da mesa se mostra desconstruída.[33]

Escher subverteu propositalmente as leis da perspectiva, a fim de criar ilusões visuais por meio de ambiguidades, como pode ser visto na litografia Queda de água de 1961.[34]

Na pintura de Van Eyck, o espelho ao fundo contém um processo de perspectiva curvilínea.
Cena do SimCity.
Mandarino, Perspectiva quadridimensional (1997).
Holografia.

Processos contemporâneos

Existem processos de perspectiva que abordam os elementos do sistema projetivo de forma variada, ou seja, observador(es), plano(s) de projeção e o objeto(s) a ser(em) representado(s) diferem daquilo que foi postulado pelos métodos tradicionais.

Perspectiva curvilínea (1968)

Ver artigo principal: Perspectiva curvilínea

A perspectiva curvilínea (perspectiva esférica ou perspectiva cilíndrica) é uma processo gráfico usado para desenhar objetos em uma superfície curva (o que difere do quadro dos processos renascentistas). Artistas como Jan van Eyck e Escher (em Mão com esfera refletora) desenvolveram trabalhos com esse tipo de representação na simulação de espelhos, mas não deixaram teoria escrita sobre o método. Em 1968 um processo curvilíneo foi codificado pelos artistas André Barre e Albert Flocon no livro La Perspective curviligne[35], que foi traduzido para o Inglês, em 1987, como Curvilinear Perspective: From Visual Space to the Constructed Image.[36]

Perspectivas animadas (anos 90)

Os processos tradicionais de perspectiva foram adaptados para os programas de computação gráfica e os seus resultados aproveitados para os jogos eletrônicos de estratégia e simuladores profissionais.[37] Um dos inúmeros exemplos é a primeira versão do SimCity (com a evolução tecnológica, passou-se a utilizar cada vez mais a perspectiva isométrica no lugar da militar, o que oferecia uma maior sensação espacial, adotando-se, posteriormente, a perspectiva cônica).[38]

Perspectiva quadridimensional (1997)

Ver artigo principal: Perspectiva quadridimensional

A perspectiva quadridimensional é um processo gráfico desenvolvido pelo artista plástico Denis Mandarino, em 1997, que pode ser visto no quadríptico Observação no tempo[39]. O processo utiliza diversos pontos de vista de um observador móvel, obtidos em diferentes momentos. O método admite suportes pictóricos planos ou curvilíneos e múltiplos pontos de fuga.[40]

Perspectiva holográfica (Séc. XXI)

As projeções holográficas[41] têm sido objeto de inúmeras aparições na ficção científica escrita, televisiva e cinematográfia.[42] O holograma tornou-se substantivo concreto e cada vez mais a indústria do entretenimento têm interesse por esse tipo de produto. Os óculos especiais[43] e as telas de projeção (3D)[44], são tentativas de transcender os limites do plano de projeção (quadro). Séries de sucesso como Star Trek, Star Wars, Babylon 5, O Homem de Ferro entre muitas outras, mostram objetos ou personagens projetados num ambiente, permitindo que os entes holográficos sejam circundados por quem os observa, como se fossem esculturas ou seres vivos. Shows musicais têm utilizado hologramas em suas apresentações.[45] Esse tipo de sistema projetivo extrapola os conceitos de observador, observado e plano de projeção (quadro), ampliando os limites das projeções em perspectiva.[46]

Referências

  1. ↑ Gill, Robert W. (1989). Desenho de perspectiva. [S.l.]: Colecção Dimensões. 115 páginas. p. 59 
  2. ↑ 2,0 2,1 Panofsky, Erwin - A perspectiva como forma simbólica (1927). Trad. Elisabete Nunes. Lisboa: Edições 70, 1993. p. 69.
  3. ↑ Scaarwaärwachter, Georg - Perspectiva para arquitetos. Barcelona: Editorial Gustavo Gili S.A., 1974. p. 115.
  4. ↑ Witting, F. - Von Kunst und Christentum, Estrasburgo, 1903, vol. 8, p. 25-26.
  5. ↑ Hughes, Robert - The Shock of the New, The Mechanical Paradise, 1987, BBC.
  6. ↑ 6,0 6,1 Lessing, Gotthold Ephraim - Schriften, 1753-1755 (6 vols., rev. ed. 1771), Berlim.
  7. ↑ 7,0 7,1 Vários autores (2011). «Novas Interfaces em Comunicação e Audiovisual (p. 12-15)». Editora Lexia. Consultado em 19 de outubro de 2012 
  8. ↑ Panofsky, Erwin - A perspectiva como forma simbólica (1927). Trad. Elisabete Nunes. Lisboa: Edições 70, 1993. p.50.
  9. ↑ Panofsky, Erwin. A perspectiva como forma simbólica (1927). Trad. Elisabete Nunes. Lisboa: Edições 70, 1993. p. 135 - decoração de uma parede, de Bocoreale, "quarto estilo" sec. I, Museo Nazionali, Napoli.
  10. ↑ Nader El-Bizri (2005). «A phiosophical perspective on Alazhen's optics». Cambridge University Press. Consultado em 21 de outubro de 2012  (em inglês)
  11. ↑ Tyler, Christopher and Kubovy, Michael. «The Role of Perspective in Shaping the Renaissance». Science & art of perspective. Consultado em 21 de outubro de 2012 
  12. ↑ Taton, René & Flocon, Albert - A perspectiva. Portugal: Difusão Europeia do Livro, 1967. p. 47.
  13. ↑ Vasari, Giorgio (2011). Vidas dos artistas. [S.l.]: Martins Fontes. pp. 228 
  14. ↑ Vasari, 2011, p. 290.
  15. ↑ Vasari, 2011, p. 274.
  16. ↑ Leonardo on Painting: An Anthology of Writings, tradução para o inglês por Margaret Walker; Londres: Yale University Press, 1989, p. 52.
  17. ↑ 17,0 17,1 Aplicação do perspectógrafo a laser no ensino da perspectiva, XIV Congreso Internacional de Engenharia Gráfica, Espanha, 2002. p. 3.
  18. ↑ Capozzi, Delton - Desenho Técnico Vol. 2. Universitária, São Paulo, 2006, p. 79-80.
  19. ↑ Juan Miguel Lorente (1985). «Perspectiva con tres puntos de fuga» (PDF). Commons. Consultado em 31 de outubro de 2012 
  20. ↑ French, T. E. & Vierck, C. J. (1985). Desenho técnico e Tecnologia Gráfica. [S.l.]: Globo. p. 312 
  21. ↑ French, T. E. & Vierck, C. J. (1985). Desenho técnico e Tecnologia Gráfica. [S.l.]: Globo. p. 332-333 
  22. ↑ French, T. E. & Vierck, C. J. (1985). Desenho técnico e Tecnologia Gráfica. [S.l.]: Globo. p. 313 
  23. ↑ Machado, Ardevan - Perspectiva. São Paulo: Grêmio Politécnico, 1983, p. 207.
  24. ↑ Rodríguez de Abajo, F. Javier (2004). Tratado de Perspectiva (em español) 5 ed. [S.l.]: Editorial Donostiarra, S.A. ISBN 978-84-7063-048-4 
  25. ↑ 25,0 25,1 25,2 25,3 Dozzi, Antonio & Francisco, Daniel (1987). Desenho técnico. [S.l.: s.n.] Cap. 8 - p. 16 
  26. ↑ 26,0 26,1 B. Leupen e.a. (2007). Ontwerp en analyse. 010 Publishers, 2007. ISBN 90-6450-558-6.
  27. ↑ Audibert, Gérard. La Perspective Cavalière. Paris: Association des Profresseurs de Mathématiques de l'Enseignement Publique, 1990. (em francês)
  28. ↑ 28,0 28,1 Machado, 1983, p. 252.
  29. ↑ Petroc, Raiko (1975). Geometria descritiva com ilustrações anaglíficas. [S.l.]: Oren. p. 92 
  30. ↑ Portal São Francisco. «Claude Monet». Consultado em 21 de outubro de 2012 
  31. ↑ 31,0 31,1 31,2 Andrew Graham-Dixon (2012). Arte, o guia visual definitivo. [S.l.]: Publifolha. p. 21 
  32. ↑ Andrew Graham-Dixon (2012). Arte, o guia visual definitivo. [S.l.]: Publifolha. p. 473 
  33. ↑ Visual art Encyclopedia. «Basket of Apples». Wiki Paintings. Consultado em 22 de outubro de 2012 
  34. ↑ Ernst, Bruno (2007). O espelho mágico de M. C. Escher. [S.l.]: Taschen. pp. 51 
  35. ↑ Albert Flocon and André Barre, La Perspective curviligne, Flammarion, Éditeur, Paris, 1968
  36. ↑ Albert Flocon and André Barre, Curvilinear Perspective: From Visual Space to the Constructed Image, (Robert Hansen, translator), University of California Press, Berkely and Los Angeles, Califórnia, 1987 ISBN 0520059794
  37. ↑ Marco Antonio Garcia de Carvalho. «Computação gráfica - Projeções» (PDF). Ceset.unicamp.br. Consultado em 22 de outubro de 2012 
  38. ↑ «Sim City». Tec Toy. 17 de setembro de 2008. Consultado em 22 de outubro de 2012 [ligação inativa]
  39. ↑ M. Macho (2014). «La perspectiva cuatridimensional...». Universidade do País Basco. Consultado em 10 de novembro de 2014 
  40. ↑ Mandarino, Denis (agosto de 1997). «A perspectiva quadridimensional». Webartigos.com. Consultado em 22 de outubro de 2012 
  41. ↑ Universidade federal do Rio de Janeiro. «Interferometria holográfica». Consultado em 23 de outubro de 2012 
  42. ↑ Águeda, Carmen de (21 de agosto de 2011). «Holografias, "humanos digitais" e mais conexão nos videogames do futuro». UOL Notícias - Ciência. Consultado em 23 de outubro de 2012 
  43. ↑ Redação Terra (12 de dezembro de 2003). «Como funcionam os óculos 3D usados no cinema?». Terra - Notícias. Consultado em 24 de outubro de 2012 
  44. ↑ Redação Revista FAPESP (Abril de 2012). «Telas 3D sem óculos». FAPESP. Consultado em 24 de outubro de 2012 
  45. ↑ Portal Saga. «Holograma: da ficção científica para a realidade». Consultado em 23 de outubro de 2012. Arquivado do original em 30 de junho de 2012 
  46. ↑ Predefinição:Obra citada

Bibliografia

  • Montenegro, Gildo A. - A perspectiva dos profissionais. Ed. Edgard Blucher, São Paulo, 1990.
  • White, Gwen - Perspectiva. Trad. Conceição Jardim e Eduardo Nogueira. Lisboa: Editorial Presença, 1990.
  • Principles of holography H. M. Smith, Wiley (1976), ISBN 978-0-471-80341-6
  • Holographic Visions: A History of New Science Sean F. Johnston, Oxford University Press (2006), ISBN 0-19-857122-4

Ver também

Ligações externas

talvez você goste

Permaneça conectado

Parceiros

Dieta Cetogenica | NutriPro Saúde