Divisão por zero

A função y=1/x. Ao mesmo tempo em que x se aproxima de 0 da direita, y se aproxima do infinito (e vice-versa). Observar que dependendo de que lado percorre-se x, o limite é infinito positivo (vindo da direita) ou infinito negativo (vindo da esquerda).

Na matemática, uma divisão é chamada divisão por zero se o divisor é zero. Tal divisão pode ser formalmente expressada como $a\div 0$ = $\textstyle {\frac {a}{0}}$ no qual a é o dividendo. Um valor bem definido para essa expressão depende do contexto matemático. Para a aritmética com números reais, a expressão não possui significado.

Em programação, uma tentativa de dividir um número de ponto flutuante por zero deve resultar em infinito (${\infty }$) de acordo com o padrão IEEE 754 para pontos flutuantes. No entanto, dependendo do ambiente de programação e do tipo de número sendo dividido por zero (como o inteiro, por exemplo), é possível que: seja gerada uma exceção, seja produzida uma mensagem de erro, faça o programa terminar, resulte em infinito positivo ou negativo ou resulte em um valor especial não numérico (NaN).

Interpretação em aritmética elementar

Quando uma divisão é explicada no nível elementar, frequentemente usa-se a descrição da divisão de um conjunto de objetos em partes iguais. Como exemplo, se tem-se dez maçãs, e deseja-se distribuí-las entre cinco pessoas, cada pessoa irá receber $10\div 5$ = $\textstyle {\frac {10}{5}}$ = 2 maçãs. Se tem-se dez maçãs e deseja-se distribuir entre zero pessoas, quantas maçãs cada pessoa receberá? Uma tentativa para calcular $10\div 0$ = $\textstyle {\frac {10}{0}}$ = ${\infty }$ maçãs.

Outra maneira de entender a natureza indefinida da divisão por zero é perceber uma divisão como repetidas subtrações. Para dividir treze por cinco, pode-se subtrair cinco duas vezes, restando três. O dividendo é subtraído até que o resto seja menor que o divisor. Mas, no caso do zero, repetidas subtrações por zero nunca resultarão em um resto menor que o divisor, então a divisão não é definida.

Primeiras tentativas

Brahmasphutasiddhanta de Brahmagupta (598–668) é o primeiro texto conhecido a tratar o zero como um número e a definir operações envolvendo o zero. O autor falhou, entretanto, em sua tentativa a explicar a divisão por zero: sua definição pode ser facilmente provada a levar a absurdos algébricos. De acordo com Brahmagupta, "um número positivo ou negativo, quando divido por zero, é uma fração com o zero como denominador. O zero dividido por um número positivo ou negativo é tanto zero ou expresso como uma fração com zero como numerador. Zero dividido por zero é zero."

Em 830, Mahavira tentou sem sucesso corrigir a falha de Brahmagupta em seu livro Ganita Sara Samgraha: "um número permanece inalterado quando dividido por zero."

Bhaskara II tentou resolver o problema ao definir $\textstyle {\frac {n}{0}}=\infty$. Essa definição, apesar de fazer sentido, pode levar a paradoxos se não tratadas com cuidado.

Interpretação algébrica

É geralmente considerado entre matemáticos que uma maneira natural de interpretar a divisão por zero é primeiramente definir a divisão em termos de outras operações aritméticas. Nas regras padrão da aritmética de inteiros, racionais, reais e complexos, a divisão por zero é indefinida. A divisão por zero deve ser deixada indefinida em qualquer sistema matemático que obedece os axiomas de um corpo. A razão é que a divisão é definida como a operação inversa da multiplicação, o que significa que o valor de $\textstyle {\frac {a}{b}}$ ($a\div b$) é a solução x da equação $b\times x=a$ sempre que o valor existir e for único. Senão o valor é deixado indefinido.

Para b = 0, a equação $b\times x=a$ pode ser reescrita como $0\times x=a$ ou simplesmente 0 = a. Nesse caso, a equação $b\times x=a$ não possui solução se a é diferente de zero, e possui qualquer x como solução se a é igual a 0. Em qualquer caso, não há solução única, então $\textstyle {\frac {a}{b}}$ ($a\div b$) é indefinida.

Falácias

É possível distinguir um caso especial da divisão por zero em um argumento algébrico, levando a provas inválidas tais como 2 = 1 como a seguinte:

Assume-se:

$0\times 1=0$

$0\times 2=0$

O seguinte deve ser verdadeiro:

$0\times 1=0\times 2$

Dividindo por zero temos:

$\textstyle {\frac {0}{0}}\times 1={\frac {0}{0}}\times 2$

Simplificando, resulta-se em :

$1=2\,$

A falácia é assumir que dividir por zero é uma operação legítima com $0\div 0=1$. Apesar da maioria das pessoas provavelmente assumirem que a prova acima é falaciosa, o mesmo argumento pode ser apresentado de uma forma que torna-se mais difícil encontrar o erro. Por exemplo, se 1 é denotado por $x$, $0$ pode ser escondido em $x-x$ e $2$ escondido em $x+x$. A prova acima pode ser apresentada como:

$(x-x)\times x=x^{2}-x^{2}=0$

$(x-x)\times (x+x)=x^{2}-x^{2}=0$

Então:

$(x-x)\times x=(x-x)\times (x+x)$

Dividindo por $x-x$ temos:

$x=x+x$

E dividindo por $x$ temos:

$1=2$

Contra argumentação da prova:

Cria-se paradoxo quando se atribui várias igualdades simultâneas a uma equação.

$(x-x)\times x=x^{2}-x^{2}$

$(x-x)\times x=0$

$x^{2}-x^{2}=0$

Fazendo o cálculo de forma individual não se percebe erro lógico ao afirmar que todo número que seja dividido por si resulte em 1, inclusive zero.

Subtrações sucessivas

Toda divisão pode ser interpretada como uma sequência finita de subtrações. E, utilizando o método de subtrações sucessivas, pode-se provar que a divisão por zero é impossível. Esta operação peculiar gera uma sequência infinita de subtrações, isto é, obriga a efetuar infinitas repetições (mais conhecidas na área computacional como loops infinitos).

Passo-a-passo

1. Subtrair o dividendo pelo divisor;
2. Caso o quociente obtido seja maior ou igual ao divisor, subtrair o quociente obtido pelo divisor;
3. Repetir o segundo passo até que o quociente obtido seja menor que o divisor, encerrando o processo e tornando o atual quociente em resto.

Divisão de 18 por 18 (exemplo)

• 18 - 18 = 0 (1^a subtração)

Como a subtração foi realizada sucessivamente 1 vez, a divisão de 18 por 18 resulta em 1 com resto 0.

Divisão de 18 por 9 (exemplo)

• 18 - 9 = 9 (1^a subtração)
• 9 - 9 = 0 (2^a subtração)

Como a subtração foi realizada sucessivamente 2 vezes, a divisão de 18 por 9 resulta em 2 com resto 0.

Divisão de 18 por 6 (exemplo)

• 18 - 6 = 12 (1^a subtração)
• 12 - 6 = 6 (2^a subtração)
• 6 - 6 = 0 (3^a subtração)

Como a subtração foi realizada sucessivamente 3 vezes, a divisão de 18 por 6 resulta em 3 com resto 0.

Divisão de 18 por 4 (exemplo)

• 18 - 4 = 14 (1^a subtração)
• 14 - 4 = 10 (2^a subtração)
• 10 - 4 = 6 (3^a subtração)
• 6 - 4 = 2 (4^a subtração)

Como a subtração foi realizada sucessivamente 4 vezes, a divisão de 18 por 4 resulta em 4 com resto 2. Ou seja, $18\div 4$ resulta verdadeiramente em 4,5.

Divisão de 18 por 3 (exemplo)

• 18 - 3 = 15 (1^a subtração)
• 15 - 3 = 12 (2^a subtração)
• 12 - 3 = 9 (3^a subtração)
• 9 - 3 = 6 (4^a subtração)
• 6 - 3 = 3 (5^a subtração)
• 3 - 3 = 0 (6^a subtração)

Como a subtração foi realizada sucessivamente 6 vezes, a divisão de 18 por 3 resulta em 6 com resto 0.

Divisão de 18 por 2 (exemplo)

• 18 - 2 = 16 (1^a subtração)
• 16 - 2 = 14 (2^a subtração)
• 14 - 2 = 12 (3^a subtração)
• 12 - 2 = 10 (4^a subtração)
• 10 - 2 = 8 (5^a subtração)
• 8 - 2 = 6 (6^a subtração)
• 6 - 2 = 4 (7^a subtração)
• 4 - 2 = 2 (8^a subtração)
• 2 - 2 = 0 (9^a subtração)

Como a subtração foi realizada sucessivamente 9 vezes, a divisão de 18 por 2 resulta em 9 com resto 0.

Divisão de 18 por 1 (exemplo)

• 18 - 1 = 17 (1^a subtração)
• 17 - 1 = 16 (2^a subtração)
• 16 - 1 = 15 (3^a subtração)
• 15 - 1 = 14 (4^a subtração)
• 14 - 1 = 13 (5^a subtração)
• 13 - 1 = 12 (6^a subtração)
• 12 - 1 = 11 (7^a subtração)
• 11 - 1 = 10 (8^a subtração)
• 10 - 1 = 9 (9^a subtração)
• 9 - 1 = 8 (10^a subtração)
• 8 - 1 = 7 (11^a subtração)
• 7 - 1 = 6 (12^a subtração)
• 6 - 1 = 5 (13^a subtração)
• 5 - 1 = 4 (14^a subtração)
• 4 - 1 = 3 (15^a subtração)
• 3 - 1 = 2 (16^a subtração)
• 2 - 1 = 1 (17^a subtração)
• 1 - 1 = 0 (18^a subtração)

Como a subtração foi realizada sucessivamente 18 vezes, a divisão de 18 por 1 resulta em 18 com resto 0.

Divisão de 18 por 0 (exemplo)

• 18 - 0 = 18 (1^a subtração)
• 18 - 0 = 18 (2^a subtração)
• 18 - 0 = 18 (3^a subtração)
• 18 - 0 = 18 (4^a subtração)
• 18 - 0 = 18 (5^a subtração)
• 18 - 0 = 18 (6^a subtração)
• 18 - 0 = 18 (7^a subtração)
• 18 - 0 = 18 (8^a subtração)
• 18 - 0 = 18 (9^a subtração)
• 18 - 0 = 18 (10^a subtração)
• 18 - 0 = 18 (11^a subtração)
• 18 - 0 = 18 (12^a subtração)
• 18 - 0 = 18 (13^a subtração)
• 18 - 0 = 18 (14^a subtração)
• 18 - 0 = 18 (15^a subtração)
• 18 - 0 = 18 (16^a subtração)
• 18 - 0 = 18 (17^a subtração)
• 18 - 0 = 18 (18^a subtração)
• 18 - 0 = 18 (19^a subtração)
• 18 - 0 = 18 (20^a subtração)
• 18 - 0 = 18 (21^a subtração)
• 18 - 0 = 18 (22^a subtração)
• 18 - 0 = 18 (23^a subtração)
• 18 - 0 = 18 (24^a subtração)
• 18 - 0 = 18 (25^a subtração)
• 18 - 0 = 18 (26^a subtração)
• 18 - 0 = 18 (27^a subtração)
• 18 - 0 = 18 (28^a subtração)
• 18 - 0 = 18 (29^a subtração)
• 18 - 0 = 18 (30^a subtração)
• ...

As subtrações continuam infinitamente, pois o resultado das subtrações continuarão sendo 18 e jamais serão 0, portanto seria infinitas subtrações. Vale-se dizer que $18\div 0$ resulta em ${\infty }$.

Divisão de 0 por 0 (exemplo)

• 0 - 0 = 0 (1^a subtração)
• 0 - 0 = 0 (2^a subtração)
• 0 - 0 = 0 (3^a subtração)
• ...

As subtrações continuam infinitamente, porque o critério de encerramento ("até que o quociente obtido seja menor que o divisor") nunca é atingido. O quociente será sempre 0, ou seja, sempre igual ao divisor (0) e nunca menor. Portanto é impossível dividir zero por zero.

Três possíveis situações

Sabendo que a expressão algébrica $a\div b=c$ (a dividido por b é igual a c) equivale à expressão algébrica a = $b\times c$ (a é igual a b multiplicado por c), podemos definir as três possíveis situações encontradas ao tentar dividir algum número por zero.

Número positivo dividido por zero

• $96\div 0={\infty }$

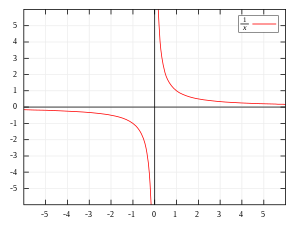
Qualquer número positivo dividido por zero resulta em infinito.

Número negativo dividido por zero

• $(-96)\div 0=({-\infty })$

Qualquer número negativo dividido por zero resulta em infinito negativo.

Zero dividido por zero

• $0\div 0=indeterminado$

Zero dividido por zero resulta em uma indeterminação, pois qualquer número (com exceção do infinito e do infinito negativo) multiplicado por zero, sempre irá resultar em zero e não é determinado o único valor de quociente para esta divisão $0\div 0$. Vale ressaltar que zero é número nulo, ou seja, não é positivo e nem negativo.

Divisão por zero na natureza

É possível encontrar a divisão por zero sendo representada pela singularidade de um buraco negro. Usando a fórmula da densidade $d={\frac {m}{v}}$, a massa de um buraco negro está contida em um volume que tende a zero, concebendo assim, a singularidade.

Ver também

• 0 (número)
• Divisão