Um buraco negro de Reissner-Nordstrøm é um buraco negro estático, com simetria esférica e com carga elétrica, o qual é definido por dois parâmetros: a massa M e a carga elétrica Q. Sua solução foi obtida, de forma independente, em 1916 e 1918 pelo matemático Hans Reissner e pelo físico teórico Gunnar Nordström às equações de campo da relatividade em torno de um objeto massivo eletricamente carregado e carente de momento angular.[1]
Descrição geométrica
O buraco negro de Reissner-Nordstrøm é uma região isotrópica que é delimitada por duas superfícies assim definíveis: uma externa chamada horizonte de eventos, e outro interno chamado horizonte de Cauchy. Estes espaços formam uma esfera perfeita, devido à carência de momento angular, em cujo centro se encontra uma singularidade espaço-temporal simples, em diferença ao caso mais geral de um buraco negro de Kerr-Newman que pode apresentar singularidades na forma de anel.
A fórmula que determina a distância desta com respeito ao respectivas horizontes depende unicamente da massa e a carga do buraco, em unidades do sistema internacional:
- [1]
Onde r é a distância de cada horizonte, M é a massa, Q é a carga elétrica e o signo determina o horizonte em questão, sendo o valor positivo para o horizonte externo e o negativo para o horizonte de Cauchy.
Relação ao parâmetro de carga Q e a massa M
Os valores que tomam a carga elétrica e a massa são muito importantes na anatomia de um buraco negro de Reissner-Nordstrøm, devido a que é sua relação a que determina o limite concreto entre seus horizontes. Existem basicamente trâs relações:
- ou, como é usual, : se parece muito ao caso do buraco negro de Schwarzschild mas com dois horizontes a uma distância razoável um do outro.
- : para este caso os horizontes se fundem, formando um horizonte contínuo que rodeia à singularidade.
- : se supõe que este caso não existe na natureza, devido a que não é comum que a carga elétrica total, dividida pelo fator do denominador, supere a massa total de um corpo, pois com isto os horizontes se anulam deixando visível a singularidade.
Além disso, existe a chamada hipótese da censura cósmica, proposta pelo matemático Roger Penrose em 1965, que não permite a existência de singularidades nuas no universo.
Trajetórias de partículas
Uma forma de estudar as caracerísticas desse espaço-tempo é analisando as geodésicas e as trajetórias de partículas carregadas em sua vizinhança.[1] Neste caso, não só a gravidade contribui para o encurvamento das trajetórias como também a força de Lorentz, cuja natureza atrativa ou repulsiva dependerá do sinal das cargas do buraco negro e da partícula-teste. As partículas carregadas interagem gravitacional e eletricamente com o buraco negro carregado.
A dinâmica das partículas-teste nesse espaço-tempo pode ser derivada da seguinte lagrangiana:
onde e são a massa e a carga da partícula-teste, é o potencial vetor e é um parâmetro afim.
As quantidades conservadas ao longo do movimento são dadas por:
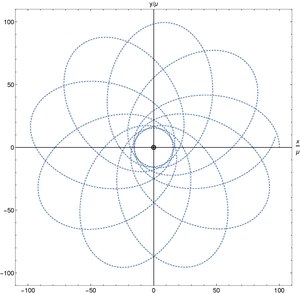
As trajetórias são trajetórias planares de forma que pode-se restringir ao plano equatorial . A equação de movimento geral é então dada por:
onde para trajetórias nulas ou tipo-tempo, respectivamente. Na figura, é mostrado um exemplo de órbita ligada de uma partícula carregada com carga de mesmo sinal da do buraco negro.
Desenvolvimentos
São identificadas as características a serem observáveis de tais corpos celestes e calculados seus possíveis espectros pela busca de uma quantização de tal fenômeno,[2] assim como o uso de técnicas Hamiltonianas.[3]
Teorizações sobre o processo de tunelamento de uma partícula próxima a um horizonte de buraco negro e sua relação com a radiação Hawking, com considerações de que se tal partícula com momento angular tunela pelo horizonte de eventos de um buraco negro de Reissner-Nordstrom, este buraco negro se transformaria num buraco negro de Kerr-Newman.[4]
Trata-se também do comportamento de férmions carregados, sua dispersão, por buracos negros de Reissner-Nordström fortemente magnéticos.[5]
Bibliografia
- Misner, C. W.; Thorne, K. S.; and Wheeler, J. A. Gravitation. San Francisco, CA: W. H. Freeman, pp. 840–841 and 878, 1973.
- Nordström, G. "On the Energy of the Gravitational Field in Einstein's Theory." Proc. Kon. Ned. Akad. Wet. 20, 1238-1245, 1918.
- Reissner, H. "Über die Eigengravitation des elektrischen Feldes nach Einsteinschen Theorie." Ann. Phys. 59, 106-120, 1916.
- Shapiro, S. L. and Teukolsky, S. A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects. New York: Wiley, p. 357, 1983.
Referências
- ↑ 1,0 1,1 Brito, João P. B.; Bernar, Rafael P.; Benone, Carolina L.; Crispino, Luís C. B. (15 de junho de 2020). «Movimento de partículas-teste no espaço-tempo de Reissner-Nordström». Revista Brasileira de Ensino de Física (em português). ISSN 1806-1117. doi:10.1590/1806-9126-RBEF-2020-0015. Consultado em 27 de abril de 2022
- ↑ Peter Breitenlohner, Dieter Maison; Quantization of the Reissner-Nordström Black Hole (1998) - citeseer.ist.psu.edu (em inglês)
- ↑ C. Dappiaggi, S. Raschi; Spectroscopy of an AdS Reissner-Nordstrom black hole; Int.J.Mod.Phys. D15 (2006) 439 - arxiv.org (em inglês)
- ↑ Liu, Wenbiao; Quantum tunneling makes a Reissner-Nordstrom black hole turn into a Kerr-Newman black hole under angular momentum conservation; Astrophysics and Space Science, Volume 310, Numbers 1-2, July 2007 , pp. 81-84(4) - www.ingentaconnect.com (em inglês)
- ↑ STROMINGER A., TRIVEDI S. P.; Information consumption by Reissner-Nordström black holes; Physical review. D. Particles and fields 1993, vol. 48, no12, pp. 5778-5783; ISSN 0556-2821 - cat.inist.fr (em inglês)

























 " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">


