Função (matemática)

Para outros significados de função, veja função (desambiguação).

Introdução

O conceito de uma função é uma generalização de uma noção comum de uma "fórmula matemática". Funções descrevem relações matemáticas especiais entre dois objetos, x e y=f(x). O objeto x é chamado o argumento da função f e o objeto y depende de x.

Intuitivamente, uma função é uma maneira de assumir para cada valor do argumento x um único valor da função f(x). Isto pode ser especificado através de uma fórmula, um relacionamento, e/ou uma regra. Este conceito é determinístico, sempre produz o mesmo resultado a partir de uma mesma entrada (a generalização aos valores aleatórios é chamada de função estocástica). Uma função pode ser vista como uma "máquina" ou "caixa preta" que converte entradas válidas em saídas de forma unívoca.

O tipo de função mais comum é aquele onde o argumento e o valor da função são ambos numéricos, o relacionamento entre os dois é expresso por uma fórmula e o valor da função é obtido através da substituição direta dos argumentos. Considere o exemplo

$f(x)=x^{2}$

Que resulta em qualquer valor de x ao quadrado.

Uma generalização direta é permitir que funções dependam não só de um único valor, mas de vários. Por exemplo,

$g(x,y)=xy$

recebe dois números x e y e resulta no produto deles, xy.

De acordo como uma função é especificada, ela pode ser chamada de função explícita (como no exemplo acima) ou função implícita, como em

$xf(x)=1$

que implicitamente especifica a função

$f(x)=1/x$

Veja também Como especificar uma função.

Vimos que a noção intuitiva de funções não se limita a computações usando apenas números e nem mesmo se limita a computações; a noção matemática de funções é mais geral e não se limita a situações envolvendo números. Em vez disso, uma função liga um "domínio" (conjunto de valores de entrada) de tal forma que a cada elemento do domínio está associado exactamente um elemento do codomínio. As funções são definidas abstractamente com certas relações, como veremos adiante. Por causa de sua generalização, funções aparecem em muitos contextos matemáticos, e muitos campos da matemática baseiam-se no estudo de funções.

Pode notar-se que as palavras "função", "mapeamento", "mapear" e "transformar" são geralmente usadas como sinônimos. Além disso, funções podem ocasionalmente ser referidas como funções bem definidas ou função total (Veja a seção "Definição Formal").

História

Como um termo matemático, "função" foi introduzido por Leibniz em 1694, para descrever quantidades [[relacionadas] a uma curva; tais como a inclinação da curva ou um ponto específico da dita curva. Funções relacionadas à curvas são atualmente chamadas funções diferenciáveis e são ainda o tipo de funções mais encontrado por não-matemáticos. Para este tipo de funções , pode-se falar em limites e derivadas;ambos sendo medida da mudança nos valores de saída associados à variação dos valores de entrada, formando a base do cálculo infinitesimal.

A palavra função foi posterioirmente usada porEuler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos;i.e:y = F(x). Ampliando a definição de funções, os matemáticos foram capazes de estudar " estranhos" objetos matemáticos tais como funções que não são diferenciáveis em qualquer de seus pontos. Tais funções, inicialmente tidas como puramente imaginárias e chamadas genericamente de "monstros" ,foram já no final do século XX, identificadas como importantes para a construção de modelos físicos de fenômenos tais como o movimento Browniano .

Durante o Século XIX, os matemáticos começaram a formalizar todos os diferentes ramos da matemática. Weierstrass defendia que se construisse o cálculo infinitesimal sobre a Aritmética ao invés de sobre a Geometria, o que favorecia a definição de Euler em relação à de Leibniz (veja aritmetização da análise). Mais para o final do século, os matemáticos começaram a tentar formalizar toda a Matemática usando Teoria de Conjuntos,e eles conseguiram obter definições de todos os objetos matemáticos em termos do conceito de conjunto. Foi Dirichlet quem criou a definição "formal" de função moderna.

Na definição de Dirichlet, uma função é um caso especial de uma relação, relação é um conjunto de pares ordenados, onde cada elemento do par pertence a um dos conjuntos relacionados(Nas relações não existem restrições quanto à lei de correspondência entre os elementos dos conjuntos, já para as funções é costume introduzir restrições). Na maioria dos casos de interesse prático, entretanto, as diferenças entre as definições moderna e de Euler são desprezáveis.

Definição Formal

Considere dois conjuntos X e Y. Uma função f de X em Y:

$f:X\rightarrow Y$

relaciona com cada elemento x em X, um único elemento y=f(x) em Y.

Outra maneira de dizer isto é afirmar que f é uma relação binária entre os dois conjuntos tal que:

1. f é unívoca: se y = f(x) e z = f(x), então y = z.
2. f é total: para todos x em X, existe um y em Y tal que y = f(x).

Se a segunda condição é atendida, mas a primeira não, temos uma função multivaluada, o termo função multívoca é, por vezes utilizado na mesma acepção.

Se a primeira condição é atendida, mas a segunda não, temos uma função parcial.

Considere as três funções seguintes:

Arquivo:NotMap1.png	Esta não é uma função, pois o elemento 3 em X é associado com dois elementos (b e c) em Y (a função não é funcional). Este é um exemplo de função multivaluada.
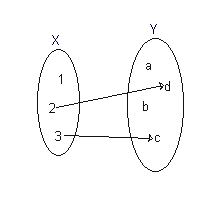	Esta não é uma função, pois o elemento 1 em X não é associado com ao menos um elemento em Y. Este é um exemplo de função parcial.
Arquivo:Mathmap.png	Esta é uma função (no caso, uma função discreta). Ela pode ser definida explicitamente pela expressão: $f(x)=\left\{{\begin{matrix}a,&{\mbox{se }}x=1\\d,&{\mbox{se }}x=2\\c,&{\mbox{se }}x=3.\end{matrix}}\right.$

Domínio, contradomínio e imagem

Função x², definida para { -3,-2,-1,0 }. Observar o conjunto domínio (D), contradomínio (CD) e imagem (delineado pela linha tracejada).

São três conjuntos especiais associados à função. O domínio é o conjunto A do exemplo dado no início deste capítulo: contém todos os elementos x para os quais a função deve ser definida. Já o conjunto B do exemplo é o contradomínio: o conjunto que contém os elementos que podem ser relacionados a elementos do domínio.

Também define-se o conjunto imagem como o conjunto de valores que efetivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio.