Função (matemática)

A palavra "função" tem vários significados em várias áreas:

• Em sociologia, funções sociais são a base do functionalismo.
• Em ciência da computação, uma função é um subprograma ou subrotina. Veja também em Programação funcional.
• No design a função é o que define o uso final ou objetivo de um objeto, produto, peça ou abstração.
• Em química , função química é um conjunto de substâncias com características semelhantes
• Esta página versa sobre funções matemáticas (a seguir).

Introdução

O conceito de uma função é uma generalização de uma noção comum de uma "fórmula matemática". Funções descrevem relações matemáticas especiais entre dois objetos, x e y=f(x). O objeto x é chamado o argumento da função f e o objeto y depende de x.

Intuitivamente, uma função é uma maneira de assumir para cada valor do argumento x um único valor da função f(x). Isto pode ser especificado através de uma fórmula, um relacionamento, e/ou uma regra. Este conceito é determinístico, sempre produz o mesmo resultado a partir de uma mesma entrada (a generalização aos valores aleatórios é chamada de função estocástica). Uma função pode ser vista como uma "máquina" ou "caixa preta" que converte entradas válidas em saídas de forma unívoca.

O tipo de função mais comum é aquele onde o argumento e o valor da função são ambos numéricos, o relacionamento entre os dois é expresso por uma fórmula e o valor da função é obtido através da substituição direta dos argumentos. Considere o exemplo

$f(x)=x^{2}$

Que resulta em qualquer valor de x ao quadrado.

Uma generalização direta é permitir que funções dependam não só de um único valor, mas de vários. Por exemplo,

$g(x,y)=xy$

recebe dois números x e y e resulta no produto deles, xy.

De acordo como uma função é especificada, ela pode ser chamada de função explícita (como no exemplo acima) ou função implícita, como em

$xf(x)=1$

que implicitamente especifica a função

$f(x)=1/x$

Veja também Como especificar uma função.

Vimos que a noção intuitiva de funções não se limita a computações usando apenas números e nem mesmo se limita a computações; a noção matemática de funções é mais geral e não se limita a situações envolvendo números. Em vez disso, uma função liga um "domínio" (conjunto de valores de entrada) de tal forma que a cada elemento do domínio está associado exactamente um elemento do codomínio. As funções são definidas abstractamente com certas relações, como veremos adiante. Por causa de sua generalização, funções aparecem em muitos contextos matemáticos, e muitos campos da matemática baseiam-se no estudo de funções.

Pode notar-se que as palavras "função", "mapeamento", "mapear" e "transformar" são geralmente usadas como sinônimos. Além disso, funções podem ocasionalmente ser referidas como funções bem definidas ou função total (Veja a seção "Definição Formal").

História

Como um termo matemático, "função" foi introduzido por Leibniz em 1694, para descrever quantidades [[relacionadas] a uma curva; tais como a inclinação da curva ou um ponto específico da dita curva. Funções relacionadas à curvas são atualmente chamadas funções diferenciáveis e são ainda o tipo de funções mais encontrado por não-matemáticos. Para este tipo de funções , pode-se falar em limites e derivadas;ambos sendo medida da mudança nos valores de saída associados à variação dos valores de entrada, formando a base do cálculo infinitesimal.

A palavra função foi posterioirmente usada porEuler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos;i.e:y = F(x). Ampliando a definição de funções, os matemáticos foram capazes de estudar " estranhos" objetos matemáticos tais como funções que não são diferenciáveis em qualquer de seus pontos. Tais funções, inicialmente tidas como puramente imaginárias e chamadas genericamente de "monstros" ,foram já no final do século XX, identificadas como importantes para a construção de modelos físicos de fenômenos tais como o movimento Browniano .

Durante o Século XIX, os matemáticos começaram a formalizar todos os diferentes ramos da matemática. Weierstrass defendia que se construisse o cálculo infinitesimal sobre a Aritmética ao invés de sobre a Geometria, o que favorecia a definição de Euler em relação à de Leibniz (veja aritmetização da análise). Mais para o final do século, os matemáticos começaram a tentar formalizar toda a Matemática usando Teoria de Conjuntos,e eles conseguiram obter definições de todos os objetos matemáticos em termos do conceito de conjunto. Foi Dirichlet quem criou a definição "formal" de função moderna.

Na definição de Dirichlet, uma função é um caso especial de uma relação, que é um conjunto. Na maioria dos casos de interesse prático, entretanto, as diferenças entre as definições moderna e de Euler são desprezáveis.

Definição Formal

Considere dois conjuntos X e Y. Uma função f de X em Y:

$f:X\rightarrow Y$

relaciona com cada elemento x em X, um único elemento y=f(x) em Y.

Outra maneira de dizer isto é afirmar que f é uma relação binária entre os dois conjuntos tal que:

1. f é funcional: se y = f(x) e z = f(x), então y = z.
2. f é total: para todos x em X, existe um y em Y tal que y = f(x).

Se a segunda condição é atendida, mas a primeira não, temos uma função multivaluada.

Se a primeira condição é atendida, mas a segunda não, temos uma função parcial.

Considere as três funções seguintes:

Arquivo:NotMap1.png	Esta não é uma função, pois o elemento 3 em X é associado com dois elementos (b e c) em Y (a função não é funcional). Este é um exemplo de função multivaluada.
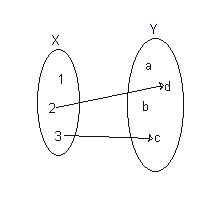	Esta não é uma função, pois o elemento 1 em X não é associado com ao menos um elemento em Y. Este é um exemplo de função parcial.
Arquivo:Mathmap.png	Esta é uma função (no caso, uma função discreta). Ela pode ser definida explicitamente pela expressão: $f(x)=\left\{{\begin{matrix}a,&{\mbox{se }}x=1\\d,&{\mbox{se }}x=2\\c,&{\mbox{se }}x=3.\end{matrix}}\right.$

Domínios, Contra-domínios e Imagens

X, the set of input values, is called the domain of f and Y, the set of possible output values, is called the codomain. The range of f is the set of all actual outputs {f(x) : x in the domain}. Beware that sometimes the codomain is wrongly called the range because of a failure to distinguish between possible and actual values.

In computer science, specifying the datatypes of the arguments and return values sets the domain and codomain (respectively) of a subprogram. So the domain and codomain are constraints imposed initially on a function; on the other hand the range has to do with how things turn out in practice.

Gráfico de uma Função

The graph of a function f is the collection of all points(x, f(x)), for all x in set X. In the example of the discrete function, the graph of f is {(1,a),(2,d),(3,c)}. There are theorems formulated or proved most easily in terms of the graph, such as the closed graph theorem.

If X and Y are real lines, then this definition coincides with the familiar sense of graph. Below is the graph of a cubic function, which is a curve:

[[Image::cubicpoly.png]]

Note that since a relation on the two sets X and Y is usually formalized as a subset of X×Y, the formal definition of function actually identifies the function f with its graph.

Imagens and preimages

The image of an element x∈X under f is the output f(x).

The image (or direct image) of A⊂X under f is the subset of Y defined by

f(A) := {f(x) : x in A}.

Notice that the range of f is the image f(X) of its domain. In our example of discrete function, the image of {2,3} under f is f({2,3})={c,d} and the range of f is {a,c,d}.

The preimage of y∈Y is the set f⁻¹(y)={x∈X : f(x)=y}. If the set is a singleton {x}, then we simply say that x=f⁻¹(y) is the preimage of y.

The preimage (or inverse image) of B ⊂ Y under f is the subset of X defined by

f ⁻¹(B) := {x in X : f(x)∈B}.

In our example of discrete function, the preimage of {a,b} is f ⁻¹({a,b})={1}.

Note that with this definiton, f ^-1 becomes a function whose domain is the set of all subsets of Y (also known as the power set of Y) and whose codomain is the power set of X'.

Some consequences that follow immediately from these definitions are:

• f(A₁ ∪ A₂) = f(A₁) ∪ f(A₂).
• f(A₁ ∩ A₂) ⊆ f(A₁) ∩ f(A₂).
• f ⁻¹(B₁ ∪ B₂) = f ⁻¹(B₁) ∪ f ⁻¹(B₂).
• f ⁻¹(B₁ ∩ B₂) = f ⁻¹(B₁) ∩ f ⁻¹(B₂).
• f(f ⁻¹(B)) ⊆ B.
• f ⁻¹(f(A)) ⊇ A.

The results relating images and preimages to the algebra of intersection and union work for any number of sets, not just for 2.

Funções Injectores, Sobrejetoras e Bijetoras

Several types of functions are very useful, deserve special names:

• injective (one-to-one) functions send different arguments to different values; in other words, if x and y are members of the domain of f, then f(x) = f(y) if and only if x = y. Our example is an injective function.
• surjective (onto) functions have their range equal to their codomain; in other words, if y is any member of the codomain of f, then there exists at least one x such that f(x) = y.
• bijective functions are both injective and surjective; they are often used to show that the sets X and Y are "the same" in some sense.

Exemplos de Funções

(More can be found at List of functions.)

• The relation wght between persons in the United States and their weights.
• The relation between nations and their capitals.
• The relation sqr between natural numbers n and their squares n².
• The relation nlog between positive real numbers x and their natural logarithms ln(x). Note that the relation between real numbers and their natural logarithms is not a function because not every real number has a natural logarithm; that is, this relation is not total and is therefore only a partial function.
• The relation dist between points in the plane R² and their distances from the origin (0,0).
• The relation grav between a point in the punctured plane R² \ {(0,0)} and the vector describing the gravitational force that a certain mass at that point would experience from a certain other mass at the origin (0,0).

Most commonly used types of mathematical functions involving addition, division, exponents, logarithms, multiplication, polynomials, radicals, rationals, subtraction, and trigonometric expressions. They are sometimes collectively referred as Elementary functions -- but the meaning of this term varies among different branches of mathematics. Example of non-elementary functions are Bessel functions and gamma functions.

n-ary function: function of several variables

Functions in applications are often functions of several variables: the values they take depend on a number of different factors. From a mathematical point of view all the variables must be made explicit in order to have a functional relationship - no 'hidden' factors are allowed. Then, again from the mathematical point of view, there is no qualitative difference between functions of one and of several variables. A function of three real variables is just a function that applies to triples of real numbers. The following paragraph says this in more formal language.

If the domain of a function is a subset of the Cartesian product of n sets then the function is called an n-ary function. For example, the relation dist has the domain R × R and is therefore a binary function. In that case dist((x,y)) is simply written as dist(x,y).

Another name applied to some types of functions of several variables is operation. In abstract algebra, operators such as "*" are defined as binary functions; when we write a formula such as x*y in this context, we are implicitly invoking the function *(x,y), but writing it in a convenient infix notation.

An important theoretical paradigm, functional programming, takes the function concept as central. In that setting, the handling of functions of several variables becomes an operational matter, for which the lambda calculus provides the basic syntax. The composition of functions (see under composing functions immediately below) becomes a question of explicit forms of substitution, as used in the substitution rule of calculus. In particular, a formalism called currying can be used to reduce n-ary functions to functions of a single variable.

Funções Compostas

The functions f: X → Y and g: Y → Z can be composed by first applying f to an argument x and then applying g to the result. Thus one obtains a function g o f: X → Z defined by (g o f)(x) := g(f(x)) for all x in X. As an example, suppose that an airplane's height at time t is given by the function h(t) and that the oxygen concentration at height x is given by the function c(x). Then (c o h)(t) describes the oxygen concentration around the plane at time t.

If Y⊂X then f may compose with itself; this is sometimes denoted f ². (Do not confuse it with the notation commonly seen in trigonometry.) The functional powers f of ⁿ = f ⁿ o f = f ⁿ⁺¹ for natural n follow immediately. On their heels comes the idea of functional root; given f and n, find a g such that gⁿ=f. (Feynman illustrated practical use of functional roots in one of his anecdotal books. <which?> Tasked with building an analogue arctan computer and finding its parts overstressed, he instead designed a machine for a functional root <fifth?> of arctan and chained enough copies to make the arctan machine.)

Função inversa

If a function f:X→Y is bijective then preimages of any element y in the codomain Y is a singleton. A function taking y∈Y to its preimage f⁻¹(y) is a well-defined function called the inverse of f and is denoted by f⁻¹.

An example of an inverse function, for f(x) = x², is f(x)⁻¹ = √x. Likewise, the inverse of 2x is x/2. The inverse function is the function that "undoes" its original.

Pointwise operations

If f: X → R and g: X → R are functions with common domain X and codomain is a ring R, then one can define the sum function f + g: X → R and the product function f × g: X → R as follows:

(f + g)(x) := f(x) + g(x);

(f × g)(x) := f(x) × g(x);

for all x in X.

This turns the set of all such functions into a ring. The binary operations in that ring have as domain ordered pairs of functions, and as codomain functions. This is an example of climbing up in abstraction, to functions of more complex types.

By taking some other algebraic structure A in the place of R, we can turn the set of all functions from X to A into an algebraic structure of the same type in an analogous way.

References

• Visual Calculus by Lawrence S. Husch, University of Tennessee (2001)