imported>E2mb0t m (User-controlled Bot: table syntax updated) |
imported>LeonardoRob0t m (Bot: Mudança automática (-{{msg:stub}} +{{esboço}})) |
||
| Linha 1: | Linha 1: | ||
{{ | {{esboço}} | ||
{{msg:emtraducao2}} | {{msg:emtraducao2}} | ||
Uma '''onda''' é uma perturbação que se propaga através do [[espaço]]. Uma onda pode propagar-se através do espaço, como no caso das [[electromagnetismo|ondas electromagnéticas]], ou através de matéria líquida, sólida ou gasosa. Neste último caso, as partículas do meio oscilam à volta de um ponto médio, mas não se deslocam. | Uma '''onda''' é uma perturbação que se propaga através do [[espaço]]. Uma onda pode propagar-se através do espaço, como no caso das [[electromagnetismo|ondas electromagnéticas]], ou através de matéria líquida, sólida ou gasosa. Neste último caso, as partículas do meio oscilam à volta de um ponto médio, mas não se deslocam. | ||
Edição das 12h20min de 30 de novembro de 2004
Predefinição:Emtraducao2 Uma onda é uma perturbação que se propaga através do espaço. Uma onda pode propagar-se através do espaço, como no caso das ondas electromagnéticas, ou através de matéria líquida, sólida ou gasosa. Neste último caso, as partículas do meio oscilam à volta de um ponto médio, mas não se deslocam.
A wave is a disturbance that propagates. Apart from electromagnetic radiation, and probably gravitational radiation, which can travel through vacuum, waves exist in a medium (which on deformation is capable of producing elastic restoring forces) through which they travel and can transfer energy from one place to another without any of the particles of the medium being displaced permanently; i.e. there is no associated mass transport. Instead, any particular point oscillates around a fixed position.
Uma onda pode ser longitudinal quando a oscilação das partículas ocorre na direcção da propagação da onda ou tranversal quando as partículas oscilam na direcção perpendicular à direcção de propagação da onda.
Media
A medium that can have a wave propogate through it is classified as the following:
- A linear medium if different waves at any particular point in the medium can be added,
- A bounded medium if it is finite in extent,otherwise unbounded.
- A uniform medium if its physical properties are unchanged at different points,
- A isotropic medium if its physical properties are same in different directions.
Examples of waves
- Sea-waves, which are perturbations that propagate through water (see also surfing and tsunami).
- Sound - a mechanical wave that propagates through air, liquid or solids, and is of a frequency detected by the auditory system. Similar are seismic waves in earthquakes, of which there are the S, P and L kinds.
- Light, radio waves, x-rays, etc. make up electromagnetic radiation. In this case propagation is possible without a medium, through vacuum.
Characteristic properties
All waves have common behaviour under a number of standard situations. All waves can experience the following:
- Reflection - when a wave turns back from the direction it was travelling, due to hitting a reflective material.
- Refraction - the change of direction of waves due to them entering a new medium.
- Diffraction - the spreading out of waves, for example when they travel through a small slit.
- Interference - the addition of two waves that come in to contact with each other.
- Dispersion - the splitting up of a wave up depending on frequency.
Transverse and longitudinal waves
| Arquivo:Elliptical trajectory on ripples.png |
| " When an object bobs up and down
on a |
Transverse waves are those with vibrations perpendicular to the wave's direction of travel; examples include waves on a string and electromagnetic waves. Longitudinal waves are those with vibrations along the wave's direction of travel; examples include sound waves.
Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow elliptical paths.
Polarization
Transverse waves can be polarized. Unpolarised waves can oscillate in any direction in the plane perpendicular to the direction of travel, while polarized waves oscillate in only one direction perpendicular to the line of travel.
Physical description of a wave
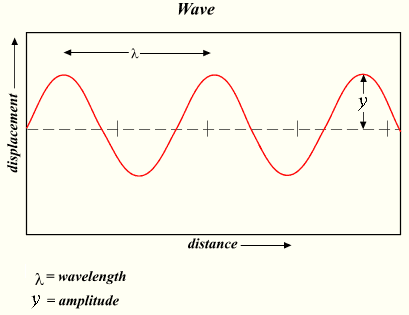
Waves can be described using a number of standard variables including: frequency, wavelength, amplitude and period.
The amplitude of a wave is the measure of the magnitude of the maximum disturbance in the medium during one wave cycle, and is measured in units depending on the type of wave. For examples, waves on a string have an amplitude expressed as a distance (meters), sound waves as pressure (pascals) and electromagnetic waves as the amplitude of the electric field (volts/meter). The amplitude may be constant (in which case the wave is a c.w. or continuous wave) or may vary with time and/or position. The form of the variation of amplitude is called the envelope of the wave.
The period (T) is the time for one complete cycle for an oscillation of a wave. The frequency (F) is how many periods per unit time (for example one second) and is measured in hertz. These are related by:
- .
When waves are expressed mathematically, the angular frequency (ω, radians/second) is often used; it is related to the frequency f by:
- .
Travelling waves
Waves that remain in one place are called standing waves - eg vibrations on a violin string. Waves that are moving are called travelling waves, and have a disturbance that varies both with time t and distance z. This can be expressed mathematically as:
,
where A(z,t) is the amplitude envelope of the wave, k is the wave number and φ is the phase. The velocity v of this wave is given by:
,
where λ is the wavelength of the wave.
The wave equation
In the most general sense, not all waves are sinusoidal. One example of a non-sinusoidal wave is a pulse that travels down a rope resting on the ground. In the most general case, any function of x, y, z, and t that is a non-trivial solution to the wave equation is a wave. The wave equation is a differential equation which describes a harmonic wave passing through a certain medium. The equation has different forms depending on how the wave is transmitted, and on what medium. A non-linear wave-equation can cause mass transport.
The Schrödinger equation describes the wave-like behaviour of particles in quantum mechanics. Solutions of this equation are wave functions which can be used to describe the probability density of a particle.
See also
- Capillary waves
- Demonstrating sound waves on an Oscilloscope
- Doppler effect
- Group velocity
- Phase velocity
- Ripple tank
- Standing wave
- Audience wave
- Ocean surface wave
ar:موجة da:Bølge de:Welle (Physik) en:Wave eo:Ondo fr:Onde it:Onda (fisica) ja:波 nds:Bülg nl:Golf (natuurkunde) pl:Fala (fizyka) simple:Wave sl:Valovanje








 " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">


