Teoria dos grafos

Predefinição:Manutenção/Categorizando por assunto Teoria de Grafos

teoria dos Grafos é o ramo da matemática que estuda as propriedades de grafos.

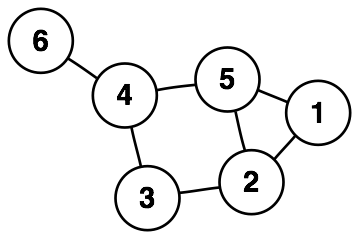Um grafo com 6 vértices e 7 arestas.

Um grafo é um conjunto de pontos, chamados vértices (ou nodos), conectados por linhas, chamadas de arestas (ou arcos). A nomenclatura de nodos e arcos está caindo em desuso.

Dependendo da aplicação, arestas podem ou não ter direção, pode ser permitido ou não arestas ligarem um vértice a ele próprio e vértices e/ou arestas podem ter um peso (numérico) associado. Se as arestas têm uma direção associada (indicada por uma seta na representação gráfica) temos um grafo direcionado, ou dígrafo

Estruturas que podem ser representadas por grafos estão em toda parte, e muitos problemas de interesse prático podem ser formulados como questões sobre certos grafos. Por exemplo, a estrutura de links da Wikipedia pode ser representada por um digrafo: os vértices são os artigos da Wikipedia e existe uma aresta do artigo A para o artigo B se e somente se A contém um link para B. Digrafos são também usados para representar máquinas de estado finito. o desenvolvimento de algoritmos para manipular grafos é um importante tema da ciência da computação.

Definições de Grafos e Dígrafos

Na literatura, as definições básicas da teoria dos grafos varia bastante. Aqui estão as convenções usadas nesta enciclopédia.

A directed graph (also called digraph or quiver) consists of

a set V of vertices, and

a set E of edges, and

maps s, t : E → V, where s(e) is the source and t(e) is the target of the directed edge e.

An undirected graph (or graph for short) is given by

a set V of vertices,

a set E of edges,

a function w : E → P(V) which associates to each edge a two- or one-element subset of V, interpreted as the endpoints of the edge.

In a weighted graph or digraph, an additional function E → R associates a value with each edge, which can be considered its "cost"; such graphs arise in optimal route problems such as the traveling salesman problem.

"Graphical" representation (graph layout)

Graphs are often represented "graphically" as follows: draw a dot for every vertex, and for every edge draw an arc connecting its endpoints. If the graph is directed, indicate the endpoint of an edge by an arrow.

Note that this graphical representation (a layout) should not be confused with the graph itself (the abstract, non-graphical structure). Very different layouts can correspond to the same graph (see http://www.aisee.com/gallery/graph23.htm ). All that matters is which vertices are connected to which others by how many edges.

Here are some examples of graph layouts:

• http://www.aisee.com/gallery
• http://www.research.att.com/sw/tools/graphviz/examples/
• http://www.tomsawyer.com/gallery/gallery.php

Glossário dos conceitos básicos de Teoria dos Grafos

Um loop num grafo ou num digrafo é uma aresta e em E cujas terminações estão no mesmo vértice. Um digrafo ou grafo é chamado simple se não tem loops e existe no máximo uma entre quaiquer dois vértices.

The example graph pictured to the right is a simple graph with vertex set V = {1, 2, 3, 4, 5, 6} and edge set E = {{1,2}, {1,5}, {2,3}, {2,5}, {3,4}, {4,5}, {4,6}} (with the map w being the identity).

An edge connects two vertices; these two vertices are said to be incident to the edge. The valency (or degree) of a vertex is the number of edges incident to it, with loops being counted twice. In the example graph vertices 1 and 3 have a valency of 2, vertices 2,4 and 5 have a valency of 3 and vertex 6 has a valency of 1. If E is finite, then the total valency of the vertices is equal to twice the number of edges. In a digraph, we distinguish the out degree (=the number of edges leaving a vertex) and the in degree (=the number of edges entering a vertex). The degree of a vertex is equal to the sum of the out degree and the in degree.

Dois vértices são considerados adjacentes se uma aresta existe entre eles. No grafo acima, os vértices 1 e 2 são adjacentes, mas os vértices 2 e 4 não são. O conjunto de vizinhos de um vértice consiste de todos os vértices adjacentes a ele. No grafo-exemplo, o vértice 1 possui 2 vizinhos: vertex 2 and node 5. For a simple graph, the number of neighbors that a vertex has coincides with its valency.

In computers, a finite directed or undirected graph (with n vertices, say) is often represented by its adjacency matrix: an n-by-n matrix whose entry in row i and column j gives the number of edges from the i-th to the j-th vertex.

Em computação, um grafo finito direcionado ou não (com, por exemplo, n vértices) é frequentemente representado pela sua matrix de adjacencias: uma matriz n-por-n cujo valor na linha i, coluna j dá o número de arestas do i-ésimo para o j-ésimo vértice.

A path is a sequence of vertices such that from each of its vertices there is an edge to the successor vertex. A path is considered simple if none of the vertices in the path are repeated. The length of a path is the number of edges that the path uses, counting multiple edges multiple times. The cost of a path in a weighted graph is the sum of the costs of the traversed edges. Two paths are independent if they do not have any vertex in common, except the first and last one.

Um caminho é uma seqüência de vértices tais que para cada um deles existe uma aresta para o seguinte. Um caminho é considerado simples se nenhum de seus vértices é repetido. O tamanho de um caminho é o número de arestas que o caminho usa, contando múltiplas arestas múltiplas vezes. O custo de um caminho em um grafo com pesos é a soma dos custos das arestas atravessadas. Dois caminhos são independentes se eles não tem nenhum vértice em comum, exceto o primeiro e o último.

In the example graph, (1, 2, 5, 1, 2, 3) is a path with length 5, and (5, 2, 1) is a simple path of length 2.

If it is possible to establish a path from any vertex to any other vertex of a graph, the graph is said to be connected. If it is always possible to establish a path from any vertex to any other vertex even after removing k-1 vertices, then the graph is said to be k-connected. Note that a graph is k-connected if and only if it contains k independent paths between any two vertices. The example graph above is connected (and therefore 1-connected), but not 2-connected.

Se é possível encontrar um caminho de um vértice qualquer para outro vértice qualquer em um grafo, o grafo é dito conexo. Se é sempre possível encontrar um caminho de qualquer vértice para qualquer vértice mesmo depois de remover quaisquer k-1 vértices distintos, então o grafo é dito k-conexo. Observe que um grafo é k-conexo se e somente se ele contém k caminhos independentes entre quaisquer dois vértices. The example graph above is connected (and therefore 1-connected), but not 2-connected.

A cycle (or circuit) is a path that begins and ends with the same vertex. Cycles of length 1 are loops. In the example graph, (1, 2, 3, 4, 5, 2, 1) is a cycle of length 6. A simple cycle is a cycle which has length at least 3 and in which the beginning vertex only appears once more, as the ending vertex, and the other vertices appear only once. In the above graph (1, 5, 2, 1) is a simple cycle. A graph is called acyclic if it contains no simple cycles.

An articulation point is a vertex whose removal disconnects a graph. A bridge is an edge whose removal disconnects a graph. A biconnected component is a maximal set of edges such that any two edges in the set lie on a common simple cycle. The girth of a graph is the length of the shortest simple cycle in the graph. The girth of an acyclic graph is defined to be infinity.

A tree is a connected acyclic simple graph. Sometimes, one vertex of the tree is distinguished, and called the root. Trees are commonly used as data structures in computer science (see tree data structure).

A forest is a set of trees; equivalently, a forest is any acyclic graph.

A subgraph of the graph G is a graph whose vertex set is a subset of the vertex set of G, whose edge set is a subset of the edge set of G, and such that the map w is the restriction of the map from G.

Um subgrafo de um grafo G é um grafo cujo conjunto dos vértices é um subconjunto do conjunto de vértices G, cujo conjunto de arestas é um subconjunto do conjunto de arstas de G, e cuja função w é uma restrição da função de G.

A spanning subgraph of a graph G is a subgraph with the same vertex set as G. A spanning tree is a spanning subgraph that is a tree. Every graph has a spanning tree.

A complete graph is a simple graph in which every vertex is adjacent to every other vertex. The example graph is not complete. The complete graph on n vertices is often denoted by K_n. It has n(n-1)/2 edges (corresponding to all possible choices of pairs of vertices).

A planar graph is one which can be drawn in the plane without any two edges intersecting. The example graph is planar; the complete graph on n vertices, for n> 4, is not planar.

An Eulerian path in a graph is a path that uses each edge precisely once. If such a path exists, the graph is called traversable. An Eulerian cycle is a cycle with uses each edge precisely once. There is a dual to this concept: a Hamiltonian path in a graph is a path that visits each vertex once and only once; and a Hamiltonian cycle is a cycle which visits each vertex once and only once. The example graph does not contain an Eulerian path, but it does contain a Hamiltonian path. While determining whether a given graph has an Eulerian path or cycle is trivial, the same problem for Hamiltonian paths and cycles is extremely hard.

The null graph is the graph whose edge set and vertex set are empty.

An independent set in a graph is a set of pairwise nonadjacent vertices. In the example above, vertices 1,3, and 6 form an independent set and 3,5, and 6 are another independent set.

A clique (pronounced "click") in a graph is a set of pairwise adjacent vertices. In the example graph above, vertices 1, 2 and 5 form a clique.

A bipartite graph is any graph whose vertices can be divided into two sets, such that there are no edges between vertices of the same set. A graph can be proved bipartite if there do not exist any circuits of odd length.

A k-partite graph or k-colorable graph is a graph whose vertices can be partitioned into k disjoint subsets such that there are no edges between vertices in the same subset. A 2-partite graph is the same as a bipartite graph.

Problemas que envolvem grafos

• Coloração de grafos: o Teorema das quatro cores

• Problemas de rota:
  • Sete pontes de Königsberg
  • árvore de recobrimento mínimo
  • Problema do caminho mínimo
  • Route inspection problem (também conhecido como o "Problema do Carteiro Chinês")
  • Problema do Caixeiro viajante

• Fluxo:
  • Teorema do mínimo corte-máximo fluxo

• reconstruction conjecture

• Problemas de Isomorfismo (casamento de grafos)
  • Canonical Labeling
  • subgraph isomorphism and monomorphisms
  • Maximal common subgraph

Algoritmos Importantes

• Dijkstra's algorithm
• Kruskal's algorithm
• Nearest neighbour algorithm
• Prim's algorithm

• Algoritmo de Dijkstra
• Algoritmo de Kruskal
• Nearest neighbour algorithm
• Algoritmo de Prim

Generalizações

In a hypergraph an edge can connect more than two vertices.

An undirected graph can be seen as a simplicial complex consisting of 1-simplices (the edges) and 0-simplices (the vertices). As such, complexes are generalizations of graphs since they allow for higher-dimensional simplices.

Every graph gives rise to a matroid, but in general the graph cannot be recovered from its matroid, so matroids are not truly generalizations of graphs.

Num hypergraph uma aresta pode conectar mais que dois grafos.

Um grafo não-direcionado pode ser visto como um simplicial complex consisting of 1-simplices (the edges) and 0-simplices (the vertices). As such, complexes are generalizations of graphs since they allow for higher-dimensional simplices.

Todo grafo gera uma matroide, mas em geral o grafo não pode ser recuperado da sua matróide, logo, matroides não são generelizações reais de grafos.

Popular graph layout tools

• http://www.research.att.com/sw/tools/graphviz/
• http://www.cs.uni-sb.de/RW/users/sander/html/gsvcg1.html
• http://www.aisee.com
• http://www.tulip-software.org

Áreas afins na Matemática

• teoria de Ramsey
• Combinatória

de:Graphentheorie en:Graph theory eo:Grafeteorio es:Teoría de los grafos fr:Théorie des graphes he:תורת הגרפים ja:グラフ理論 nl:Grafentheorie pl:Teoria grafów simple:Graph theory sv:Grafteori tr:Çizge Teorisi zh:图论