Quicksort

Predefinição:Info/Algoritmo O algoritmo quicksort é um método de ordenação muito rápido e eficiente, inventado por C.A.R. Hoare em 1960, quando visitou a Universidade de Moscovo como estudante. Naquela época, Hoare trabalhou em um projeto de tradução de máquina para o National Physical Laboratory. Ele criou o quicksort ao tentar traduzir um dicionário de inglês para russo, ordenando as palavras, tendo como objetivo reduzir o problema original em subproblemas que possam ser resolvidos mais fácil e rápido. Foi publicado em 1962 após uma série de refinamentos.

O quicksort é um algoritmo de ordenação por comparação não-estável.

O algoritmo computacional

Algumas etapas do algoritmo quicksort.

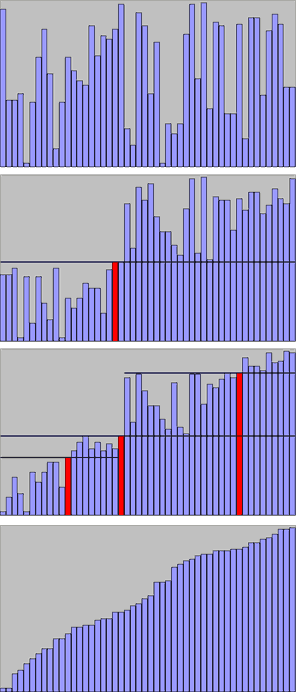
O quicksort adota a estratégia de divisão e conquista. A estratégia consiste em rearranjar as chaves de modo que as chaves "menores" precedam as chaves "maiores". Em seguida o quicksort ordena as duas sublistas de chaves menores e maiores recursivamente até que a lista completa se encontre ordenada. Os passos são:

1. Escolha um elemento da lista, denominado pivô;
2. Particiona: rearranje a lista de forma que todos os elementos anteriores ao pivô sejam menores que ele, e todos os elementos posteriores ao pivô sejam maiores que ele. Ao fim do processo o pivô estará em sua posição final e haverá duas sub listas não ordenadas. Essa operação é denominada partição;
3. Recursivamente ordene a sub lista dos elementos menores e a sub lista dos elementos maiores;

O caso base da recursão são as listas de tamanho zero ou um, que estão sempre ordenadas. O processo é finito, pois a cada iteração pelo menos um elemento é posto em sua posição final e não será mais manipulado na iteração seguinte.

A escolha do pivô e os passos do Particiona podem ser feitos de diferentes formas e a escolha de uma implementação específica afeta fortemente a performance do algoritmo.

Método de partição de Lomuto

Método atribuído a Nico Lomuto e popularizado por Bentley em seu livro Programming Pearls e por Cormen et al. no livro Introduction to Algorithms. Este método escolhe um pivô tipicamente no início ou no final do array. O Particiona recebe como parâmetro dois índices do array, lo e hi, que será a parte do array a ser particionada, então escolhe-se um índice i e percorre-se o array usando outro índice j realizando trocas, quando necessário, a fim de que todos os elementos menores ou iguais ao pivô fiquem antes do índice i e os elementos i + 1 até hi, ou j - 1, sejam maiores que o pivô . Esta é a maneira mais simples e fácil de entender, geralmente utilizada como uma introdução ao quicksort, entretanto é menos eficiente que o método Hoare. Este Método decai para O(n2) quando o array já está ordenado ou quando só possui elementos iguais. Existem várias formas para melhorar a eficiência do algoritmo através da escolha do pivô, lidar com elementos iguais, usar outros algoritmos para pequenos arrays como o Insertion sort e assim por diante.

Complexidade

• Complexidade de tempo:

Comportamento no pior caso

O pior caso de particionamento ocorre quando o elemento pivô divide a lista de forma desbalanceada, ou seja, divide a lista em duas sub listas: uma com tamanho 0 e outra com tamanho n - 1 (no qual n se refere ao tamanho da lista original). Isso pode ocorrer quando o elemento pivô é o maior ou menor elemento da lista, ou seja, quando a lista já está ordenada, ou inversamente ordenada.

Se isso acontece em todas as chamadas do método de particionamento, então cada etapa recursiva chamará listas de tamanho igual à lista anterior - 1. Teremos assim, a seguinte relação de recorrência:

$$T(n)=T(n-1)+T(0)+\theta (n)$$

$$T(n-1)+\theta (n)$$

Se somarmos os custos em cada nível de recursão, teremos uma série aritmética que tem valor $\theta (n^{2})$, assim, o algoritmo terá tempo de execução igual à $\theta (n^{2})$.

Comportamento no melhor caso

O melhor caso de particionamento acontece quando ele produz duas listas de tamanho não maior que n/2, uma vez que uma lista terá tamanho [n/2] e outra tamanho [n/2] - 1. Nesse caso, o quicksort é executado com maior rapidez. A relação de recorrência é a seguinte:

$$T(n)\leq 2T({\frac {n}{2}})+\theta (n)$$

que, a partir do teorema mestre, terá solução $T(n)=O(n*log(n))$.

• Complexidade de espaço: $\theta (log_{2}n)$ no melhor caso e no caso médio e $\theta (n)$ no pior caso. R. Sedgewick desenvolveu uma versão do quicksort com partição recursão de cauda que tem complexidade $\theta (n^{2})$ no pior caso.

Quicksort utilizando dois ou mais pivôs

Algumas etapas do algoritmo quicksort.

Dentre inúmeras tentativas de melhorar a eficiência do quicksort clássico, em 2009 foi proposto por Yaroslavskiy (2009) o Dual-Pivot Quicksort , onde são utilizados 2 pivôs, particionando um array de entrada em 3 partes. Yaroslavskiy demonstra que o uso de dois pivôs é mais eficaz, especialmente quando possui uma quantidade maior de dados de entrada, comprovando a sua vantagem em relação ao algoritmo quicksort clássico.

O algoritmo Dual-Pivot Quicksort, particiona um array de entrada de dados de diferentes dados primitivos (tais como, int, char, double float e long) em três partes, utilizando dois pivôs P1 e P2. Desse modo, estabelecem os seguintes ponteiros, L, K, G e left e right(índices para o primeiro e último elementos).

Segue abaixo a descrição do algoritmo.

1. Para pequenos vetores (tamanho < 17) utilizar o algoritmo Insertion Sort.
2. Escolha dois pivôs (P1 e P2), podemos escolher por exemplo, o primeiro (a[left]) elemento como P1 e o último como P2.
3. P1 deve ser menor do que o P2, caso contrário, eles são trocados. Então, existem as seguintes partes:
   1. Parte I: com índices elemento mais a esquerda, de left até L-1 contendo os elementos que são menores que o P1.
   2. Parte II: com índices de L até K-1 contendo os elementos maiores ou iguais a P1 e menores ou iguais a P2.
   3. Parte III: Com índices de G + 1 até o último elemento a direita, contendo os elementos superiores P2.
   4. Parte IV: contendo os elementos a ser examinados com índices de K até G
4. O próximo elemento na posição K pertencente a parte IV é comparado com os pivôs P1 e P2, e alocado na parte correspondente, I, II ou III.
5. Os ponteiros L, K e G são alterados nas direções correspondentes.
6. Os passos 4 e 5 são repetidos enquanto G se aproxima de K.
7. O pivô P1 é trocado com o último elemento da parte I, o pivô P2 é trocado com o primeiro elemento da parte III.
8. As etapas 1 e 7 são repetidas de forma recursiva para cada parte I, II e III.

Também foi demonstrado por Yaroslavskiy que para ordenação de dados primitivos é mais eficiente a utilização do quicksort de 3 partições, sendo o número médio de comparações do Dual-Pivot Quicksort é ${\mathcal {(}}{2})n\ln(n)$, e o número médio de trocas é ${\mathcal {(}}{0,8})n\ln(n)$, enquanto a versão clássica do algoritmo Quicksort possui ${\mathcal {(}}{2})n\ln(n)$ e ${\mathcal {(}}1)n\ln(n)$, respectivamente.

Uma experimento realizado pelo Budiman, Zamzami e Rachmawati (2017), foi proposto, implementado e realizado experimentos com os algoritmos quicksort clássico e quicksort com dois, três, quatro e cinco pivôs. Analisando os resultados experimentais notou-se que o quicksort com um único pivô é o mais lento entre as cinco. Em segundo lugar, analisando o uso de até 5 pivôs foi comprovado que quanto mais pivôs são utilizados em um algoritmo quicksort, mais rápido seu desempenho se torna. Em terceiro lugar, o aumento de velocidade resultante da adição de mais pivôs tende a diminuir gradualmente.

Comparação com outros algoritmos de ordenação 

Gráfico comparativo, exibindo o comportamento assintótico de alguns algorítmos de ordenação.

O quicksort é uma versão optimizada de uma árvore binária ordenada. Em vez de introduzir itens sequencialmente numa árvore explicita, o quicksort organiza-os correntemente na árvore onde está implícito, fazendo-o com chamadas recursivas à mesma. O algoritmo faz exactamente as mesmas comparações, mas com uma ordem diferente.

O algoritmo que mais se familiariza com o quicksort é o Heapsort. Para o pior caso neste algoritmo temos ${\mathcal {O}}(n\log 2n).$ Mas, o Heapsort em média trata-se de um algoritmo mais lento que o quicksort, embora essa afirmação já tenha sido muito debatida. No quicksort permanece o caso do pior caso, à exceção quando se trata de usar a variante Intro sort, que muda para Heapsort quando um pior caso é detectado. Caso se saiba à partida que será necessário o uso do heapsort é aconselhável usá-lo directamente, do que usar o introsort e depois chamar o heapsort, torna mais rápido o algoritmo.

O quicksort também compete com o Mergesort, outro algoritmo de ordenação recursiva, tendo este o benefício de ter como pior caso ${\mathcal {O}}(n\log n).$ Mergesort, ao contrário do quicksort e do Heapsort, é estável e pode facilmente ser adaptado para operar em listas encadeadas e em listas bastante grandes alojadas num tipo de acesso lento a média como um Network-Attached Storage ou num disco. Embora o quicksort possa ser operado em listas encadeadas, por vezes escolhendo um mau pivô sem acesso aleatório. A maior desvantagem do Mergesort é que quando opera em arrays, requer ${\mathcal {O}}(n)$ de espaço para o melhor caso, considerando que o quicksort com um particionamento espacial e com recursão utiliza apenas ${\mathcal {O}}(\log n)$ de espaço.

Bucket sort com dois buckets é muito parecido ao quicksort (quase idêntico), o pivô neste caso é garantidamente o valor do meio do vector.

Implementações

Pseudocódigo

Em pseudocódigo, o quicksort ordena elementos do índice $i_{0}$ até $H_{i}$ de um array A pode ser escrito da seguinte forma:

procedimento QuickSort(X[], IniVet, FimVet)
var
   i, j, pivo, aux
início
   i <- IniVet
   j <- FimVet
   pivo <- X[(IniVet + FimVet) div 2]
   enquanto(i <= j)
    |      enquanto (X[i] < pivo) faça
    |       |   i <- i + 1
    |      fimEnquanto
    |      enquanto (X[j] > pivo) faça
    |       |   j <- j - 1
    |      fimEnquanto
    |      se (i <= j) então
    |       |   aux  <- X[i]
    |       |   X[i] <- X[j]
    |       |   X[j] <- aux
    |       |   i <- i + 1
    |       |   j <- j - 1
    |      fimSe
   fimEnquanto
   se (IniVet < j) então
    |  QuickSort(X, IniVet, j)
   fimSe
   se (i < FimVet) então
    |  QuickSort(X, i, FimVet)
   fimSe
fimProcedimento

ou de outra maneira, como:

algorithm quicksort(A, lo, hi) is
    if lo < hi then
        p := particiona(A, lo, hi)
        quicksort(A, lo, p – 1)
        quicksort(A, p + 1, hi)

algorithm particiona(A, lo, hi) is
    pivot := A[hi]
    i := lo - 1    
    for j := lo to hi - 1 do
        if A[j] < pivot then
            i := i + 1
            swap A[i] with A[j]
    if pivot < A[i + 1] then
        swap A[i + 1] with A[hi]
    return i + 1

Python

Uma versão do algoritmo na linguagem Python 3 poderia ser escrito da seguinte forma:

def quick_sort(a, ini=0, fim=None):
    fim = fim if fim is not None else len(a)
    if ini < fim:
        pp = particao(a, ini, fim)
        quick_sort(a, ini, pp)
        quick_sort(a, pp + 1, fim)
    return a

def particao(a, ini, fim):
    # para uma versão com partição aleatória
    # descomente as próximas três linhas:
    # from random import randrange
    # rand = randrange(ini, fim)
    # a[rand], a[fim - 1] = a[fim - 1], a[rand]
    pivo = a[fim - 1]
    for i in range(ini, fim):
        if a[i] > pivo:
            fim += 1
        else:
            fim += 1
            ini += 1
            a[i], a[ini - 1] = a[ini - 1], a[i]
    return ini - 1

a = [8, 5, 12, 55, 3, 7, 82, 44, 35, 25, 41, 29, 17]
print(a)
print(quick_sort(a))

C++

Uma versão em C++ do primeiro pseudocódigo é expressa da seguinte maneira:

#include <iostream>

void quicksort(int values[], int began, int end)
{
	int i, j, pivo, aux;
	i = began;
	j = end-1;
	pivo = values[(began + end) / 2];
	while(i <= j)
	{
		while(values[i] < pivo && i < end)
		{
			i++;
		}
		while(values[j] > pivo && j > began)
		{
			j--;
		}
		if(i <= j)
		{
			aux = values[i];
			values[i] = values[j];
			values[j] = aux;
			i++;
			j--;
		}
	}
	if(j > began)
		quicksort(values, began, j+1);
	if(i < end)
		quicksort(values, i, end);
}

int main(int argc, char *argv[])
{
	int array[10] = {5, 8, 1, 2, 7, 3, 6, 9, 4, 10};
	for(int i = 0; i < 10; i++)
	{
		std::cout << array[i] << ' ';
	}
	std::cout << std::endl;
	quicksort(array, 0, 10);
	for(int i = 0; i < 10; i++)
	{
		std::cout << array[i] << ' ';
	}
	return 0;
}

Tendo os valores como saída respectivamente, desorganizados e organizados através da função quicksort;

5 8 1 2 7 3 6 9 4 10
1 2 3 4 5 6 7 8 9 10

Há também uma implementação padrão deste algorítimo melhor detalhada no seguinte endereço função qsort

Haskell

Uma versão do algoritmo em Haskell poderia ser escrito da seguinte forma:

quicksort :: (Ord a) => [a] -> [a]  
quicksort [] = []  
quicksort (x:xs) = 
    let smallerSorted = quicksort [a | a <- xs, a <= x]  
        biggerSorted = quicksort [a | a <- xs, a > x]  
    in  smallerSorted ++ [x] ++ biggerSorted

Partindo de uma lista inicial [10,2,5,3,1,6,7,4,2,3,4,8,9], teremos:

ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9]  
[1,2,2,3,3,4,4,5,6,7,8,9,10]

V

// ifirst_part: index of first element of partition
// ilast_part: index of last element of partition
fn partition<T>(mut array_to_sort []T, ifirst_part int, ilast_part int, compare fn (a T, b T) bool) int {
  pivot := array_to_sort[ilast_part]
  mut i := ifirst_part - 1

  for j in ifirst_part..ilast_part {
    if compare(array_to_sort[j], pivot) {
      i++
      //if i != j {
        array_to_sort[i], array_to_sort[j] = array_to_sort[j], array_to_sort[i]
        /*tmp := array_to_sort[i]
        array_to_sort[i] = array_to_sort[j]
        array_to_sort[j] = tmp*/
      //}
    }
  }

  array_to_sort[i + 1], array_to_sort[ilast_part] = array_to_sort[ilast_part], array_to_sort[i + 1]
  /*tmp := array_to_sort[i + 1]
  array_to_sort[i + 1] = array_to_sort[ilast_part]
  array_to_sort[ilast_part] = tmp*/

  return i + 1
}

// ifirst: index of first
// ilast: index of last
fn quick_sort_helper<T>(mut array_to_sort []T, ifirst int, ilast int, compare fn (a T, b T) bool) {
  if ifirst < ilast {
    partition_index := partition<T>(mut array_to_sort, ifirst, ilast, compare)

    quick_sort_helper<T>(mut array_to_sort, ifirst, partition_index - 1, compare)
    quick_sort_helper<T>(mut array_to_sort, partition_index + 1, ilast, compare)
  }
}

fn quick_sort<T>(mut array_to_sort []T, compare fn (a T, b T) bool) {
  quick_sort_helper<T>(mut array_to_sort, 0, array_to_sort.len - 1, compare)
}

fn quick_sort_clone<T>(array_to_sort []T, compare fn (a T, b T) bool) []T {
  mut array_to_sort_clone := array_to_sort.clone()

  quick_sort_helper<T>(mut array_to_sort_clone, 0, array_to_sort_clone.len - 1, compare)

  return array_to_sort_clone
}

Ver também

• Ordenação de vetor
• Merge sort
• Heapsort
• Selection sort
• Bubble sort
• Busca linear

Ligações externas

• Rápida aula de quicksort
• Sorting algorithms/Quicksort - Implementação do algoritmo em várias linguagens de programação
• QuickDualPivot.java - Algoritmo Dual Pivot Quicksort disponibilizado pelo autor