Potencial de Lennard-Jones

Potencial de Lennard-Jones para dímero de argônio

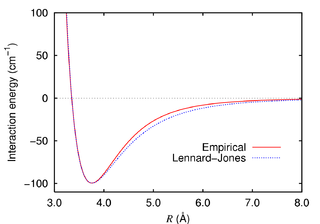
Um par de átomos neutros ou moléculas é sujeito a duas forças distintas no limite de maior e menor separação: uma força atrativa a grande distância (forças de London - forças de van der Waals) e uma força repulsiva em menores distâncias (o resultado de sobreposição de orbitais de elétrons, relacionados à força de troca do princípio de exclusão de Pauli). O potencial de Lennard-Jones (também referido como potencial L-J, potencial 6-12 ou, menos comumente, potencial 12-6) é um modelo matemático simples que representa este comportamento. Foi proposto em 1924 por John Lennard-Jones.

Descrição

O potencial L-J tem a forma

$V(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]$

onde $\,\epsilon$ é o poço de potencial e $\,\sigma$ é a distância (finita) na qual o potencial interpartícula é zero.

Estes parâmetros podem ser ajustados para reproduzir dados experimentais ou podem ser deduzidos de resultados muito precisos de cálculos de física ou química quântica. O termo

$\left({\frac {1}{r}}\right)^{12}$ descreve a repulsão e o termo $\left({\frac {1}{r}}\right)^{6}$ descreve a atração.

A função que descreve a força a que estão sujeitas as partículas é o negativo do gradiente do potencial acima descrito:

$\mathbf {F} (r)=-\nabla V(r)=-{\frac {d}{dr}}V(r){\hat {\mathbf {r} }}=4\epsilon \left(12\,{\frac {{\sigma }^{12}}{{r}^{13}}}-6\,{\frac {{\sigma }^{6}}{{r}^{7}}}\right){\hat {\mathbf {r} }}$

O potencial de Lennard-Jones é uma aproximação. A forma do termo que descreve a repulsão não tem nenhuma justificação teórica; a força repulsiva deve depender exponencialmente da distância, mas o termo da fórmula de L-J é mais conveniente devido à facilidade e eficiência de calcular r¹² como o quadrado de r⁶. Sua origem física está relacionada ao princípio de exclusão de Pauli: quando duas nuvens eletrônicas circulando os átomos iniciam a se sobrepôr, a energia do sistema aumenta abruptamente. O exponente 12 foi eleito exclusivamente por sua facilidade de cálculo.

Formas alternativas

A função do potencial de Lennard-Jones comumente se escreve da seguinte forma:

$V(r)=\epsilon \left[\left({\frac {r_{min}}{r}}\right)^{12}-2\left({\frac {r_{min}}{r}}\right)^{6}\right]$

onde

$\,r_{min}$ = $\,2^{1/6}\sigma$ é a distância na qual o potencial se encontra em um mínimo.

A formulação mais precisa, usada comumente por software de simulação, é:

$V(r)={\frac {A}{r^{12}}}-{\frac {B}{r^{6}}}$

onde

$\,A=4\epsilon \sigma ^{12}$

$\,B=4\epsilon \sigma ^{6}$

$\sigma =\left({\frac {A}{B}}\right)^{\frac {1}{6}}$

e

$\epsilon ={\frac {B^{2}}{4A}}$.

Potencial truncado

Em geral, para poupar tempo computacional, o potencial de Lennard-Jones é truncado na distância limite de $\displaystyle r_{c}=2.5\sigma$ donde

$\displaystyle V(r_{c})=V(2.5\sigma )=4\epsilon \left[\left({\frac {\sigma }{2.5\sigma }}\right)^{12}-\left({\frac {\sigma }{2.5\sigma }}\right)^{6}\right]=-0.0163\epsilon =-{\frac {1}{61.3}}\epsilon$

(1)

i.e., em $\displaystyle r_{c}=2.5\sigma$, o potencial LJ $\displaystyle V$ é aproximadamente 1/60 de seu valor mínimo $\displaystyle \epsilon$ (profundidade do potencial). Depois de $\displaystyle r_{c}$, se assinala o valor 0 ao potencial computacional.

Por outro lado, para evitar uma descontinuidade em $\displaystyle r_{c}$, como se mostra na equação 1, o potencial de LJ é desprezado ligeiramente até acima, de tal forma que o potencial computacional seja 0 exatamente na distância limite $\displaystyle r_{c}$.