Vibração

Vibração ou oscilação é qualquer movimento que se repete, regular ou irregularmente dentro de um intervalo de tempo. Na engenharia estes movimentos se processam em elementos de máquinas e em estruturas quando submetidos a ações dinâmicas. Um exemplo universal de oscilações ocorre no movimento de um pêndulo simples, intercalando entre suas posições, suas diferentes formas de energia (cinética e potencial), alternando entre tais energias.

Para realizar uma análise de vibrações é importante verificar os graus de liberdade do sistema mecânico, que consiste em identificar o número mínimo de coordenadas independentes necessárias para descrever o movimento espacial de todas partículas de um sistema em qualquer instante de tempo.

Genericamente os sistemas de vibração são compostos por um meio para armazenar energia potencial (elementos de mola), energia cinética (elemento de massa) e de dissipação de energia (amortecedores).

Grandezas físicas

Os sistemas mecânicos podem ser medidas em aceleração (unidade SI: metros por segundo ao quadrado), velocidade (unidade SI: metros por segundo) ou deslocamento (unidade SI: metros). Para a medição de vibrações em máquinas, são comuns as seguintes unidades:

aceleração: metros por segundo ao quadrado (m/s²), g (1g equivale a, aproximadamente, 9,8065 metros por segundo ao quadrado);

velocidade: metros por segundo (m/s), polegadas por segundo (ips);

deslocamento: micrômetros (1 micrometro equivale a 0,001mm), mils (1 mil equivale a 0,001").

O instrumento comumente utilizado na medição de vibrações é o coletor de dados de vibrações, que utiliza um sistema transdutor de vibrações mecânicas em sinais elétricos conhecido como acelerômetro.

Graus de liberdade

Em vibrações, o conceito de graus de liberdade consiste na definição no número mínimo de coordenadas independentes requerida para determinar completamente as posições de todas as partes de um sistema a qualquer instante.

Classificação das vibrações

Quanto à excitação

Vibrações livres

São aquelas que ocorrem sem a presença de um agente externo durante o movimento, é considerada uma vibração livre aquela que sofreu um impulso inicial e após ele, o sistema continua a vibrar livremente, por conta própria. Exemplos deste tipo de vibração: puxar uma criança em um balanço e depois soltar (note que se assemelha à ação em um pêndulo), percutir um diapasão e deixá-lo tocar.

Vibração forçada

Diz-se que um sistema mecânico sofre vibração forçada sempre que energia externa é fornecida ao sistema durante a vibração. A energia externa pode ser fornecida ao sistema por meio de uma força aplicada ou por uma excitação de deslocamento imposta. a natureza da forca aplicada ou do deslocamento pode ser definida como harmônica, não-harmônica mas periódica, não-periódica ou aleatória. A resposta de um sistema à excitação harmônica é denominada resposta harmônica. A excitação não-periódica pode ser de curta ou longa duração. A resposta de um sistema dinâmico a excitações não-periódicas aplicadas repentinamente é denominada como resposta transitória.

A resposta de um tal sistema, que é a solução da equação do movimento, sob a ação de forças, terá a mesma forma funcional que a força atuante. Isto significa que uma força harmônica produz uma vibração harmônica, uma força periódica produz uma vibração periódica, etc. Os sistemas que serão estudados são representados por equações diferenciais lineares. A solução particular da equação diferencial é, então responsável por representar este movimento. Mas a solução geral é composta de uma solução homogênea e uma solução particular. A solução homogênea representa a parcela transitória da resposta do sistema, aquela que é produzida pelas condições iniciais do movimento

Vibrações amortecidas

É quando qualquer energia é perdida e/ou dissipada na realização da oscilação, sendo por atrito ou qualquer outra força, com isso a energia da vibração se dissipa com o transcorrer do tempo, fazendo com que os níveis vibratórios diminuam progressivamente. Em muitos sistemas físicos, a quantidade de energia dissipada é muito pequena quando comparada a magnitude do sistema, e portanto é desprezada.

Vibrações não amortecidas

Nesse caso tal energia de vibração não se dissipa, isto é, não se perde energia e nem há dissipação da mesma por atrito ou outra resistência durante a vibração, de forma que o movimento vibratório permanece inalterado com o passar do tempo.

Quanto ao conhecimento da força

Vibração determinística

Ocorre quando o valor ou magnitude da excitação, seja ela força ou movimento, aplicada no sistema é conhecida em qualquer instante de tempo.

Vibração aleatória

É aquela que não pode ser prevista, os seus valores não são conhecidos. Como exemplos podemos citar a velocidade do vento e o movimento do solo durante um terremoto.

Quanto aos diversos elementos

Vibração linear

Ocorre quando todos os componentes básicos do sistema (massa, mola e amortecedor) se comportam de maneira linear, o que não ocorre com a mola depois de uma certa deformação, e portanto passa a possuir um comportamento não linear.

Vibração não linear

Quando qualquer elemento se comporta de maneira não linear no sistema, temos a vibração não linear, e portanto teremos que lidar com equações diferenciais mais complexas de se resolver e de análises melhor desenvolvidas, cujo principio da superposição não é válido como para o caso de vibrações do tipo linear. Todo sistema tende a comportar-se não linearmente com o aumento da amplitude, como no caso da mola já mencionado.

Forças de excitação

Um sistema mecânico ou estrutural sofre vibração forçada sempre que energia externa é fornecida ao sistema durante a vibração. A energia externa pode ser fornecida ao sistema por meio de uma força aplicada ou por uma excitação de deslocamento imposta. A natureza da força aplicada ou da excitação de deslocamento pode ser da natureza harmônica, não harmônica mas periódica, não periódica ou aleatória. A resposta de um sistema à excitação harmônica é denominada resposta harmônica. A excitação não-periódica pode ser de curta ou longa duração. A resposta de um sistema dinâmico a excitações não-periódicas aplicadas repentinamente é denominada resposta transitória.

Força harmônica

A vibração produzida por uma máquina rotativa desbalanceada, as oscilações de uma chaminé alta provocadas por emissão de vórtices (redemoinhos) sob vento constante e o movimento vertical de um automóvel sobre a superfície senoidal de uma estrada são exemplos de vibração excitada harmonicamente.

Considere a resposta dinâmica de um sistema com um grau de liberdade (física) sob excitação harmônica da forma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(t)=F_0e^{i(\omega t+\phi)}} ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(t)=F_0cos(\omega t +\phi)} ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(t)=F_0sen(\omega t+\phi)} . Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_0} é a amplitude, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} é a frequência e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} é o ângulo de fase da excitação harmônica. O valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} depende do valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(t)} em t=0 e normalmente é considerado zero. Sob uma excitação harmônica, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema será muito grande. Essa condição conhecida como ressonância , deve ser evitada, para impedir falha do sistema.

• Força harmônica pelo desbalanceamento rotativo

Massa desbalanceada em rotação num sistema mecânico

Massas desbalanceadas em máquinas rotativas são grandes causadoras de vibração em vários casos de engenharia, como exemplo mais clássico as rodas de um carro que quando estão desbalanceadas causam trepidações no veículo. Um sistema é dito desbalanceado quando o centro de massa desse sistema não coincide com seu centro de rotação. Uma representação simplificada dessa situação pode ser visualizada na figura ao lado. A máquina possui massa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} e há uma outra massa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} e a um amortecedor viscoso de constante de amortecimento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} . Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=mr\omega^2} . Essa força pode ser decomposta em componentes horizontal Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=mr\omega^2 cos(\omega t)} que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=mr\omega^2 sin(\omega t)} que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_p(t)=X\sin(\omega t - \phi)} . Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} a amplitude da vibração, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} a frequência de oscilação da massa desbalanceada e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} o ângulo de fase. Os valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} são

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle X=\frac{me\omega^2}{[(k - M\omega^2)^2 + (c\omega)^2]^{1/2}}}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi= \arctan(\frac{c\omega}{k - M\omega^2})}

Equação de movimento

Se uma força Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(t)} agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\overset{..}{x} + c\overset{.}{x} + kx = F(t)} . Visto que essa equação é não-homogênea, sua solução geral Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(t)} é dada pela soma da solução homogênea Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_h (t)} com a solução particular Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_p (t)} . A solução homogênea, que é a solução da equação homogênea Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\overset{..}{x} + c\overset{.}{x} + kx =0} representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_p (t)} , que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente.

Podemos perceber que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_h (t)} desaparece e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(t)} torna-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_p (t)} após algum tempo (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} .

Força periódica

Excitação que se repete em certo período, porém com intensidades diferentes. Um exemplo prático são motores de combustão interna. Se a força for periódica, mas não-harmônica, ela pode ser substituída por uma soma de funções harmônicas por da expansão da série de Fourier. Usando o princípio da superposição, a resposta do sistema pode ser determinada pela superposição das respostas às funções forçantes harmônicas individuais.

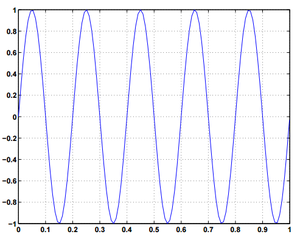
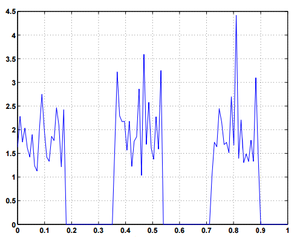
De acordo com a teoria desenvolvida pelo matemático e físico francês Jean Baptiste Joseph Fourier, qualquer função periódica F(t), com período T, pode ser representada por uma série infinita da forma abaixo:

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(t) = \frac{a_{0}}{2} + \sum_{n=1}^{\infin}(a_{n} \, cos \, n\omega_{T}t + b_{n} \, sen \, n\omega_{T}t)}

onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{T} = 2\pi/T} e onde os coeficientes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{0}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n}} , e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_{n}} são dados pelos cálculos a seguir

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{0} = \frac{2}{T} \int_{0}^{T}F(t) \, dt }

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n} = \frac{2}{T} \int_{0}^{T}F(t) \, cos \, n \omega_{T}t \, dt \,\,\,\,\,\,\, n= 1,2,\ldots}

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_{n} = \frac{2}{T} \int_{0}^{T} F(t) \, cos \, n \omega_{T}t \, dt \,\,\,\,\,\,\, n = 1,2,\ldots}

Os coeficientes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{0}} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_{n}} , são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\ddot x + c\dot x + kx = F(t) = \frac{a_{0}}{2} + \sum_{j=1}^{\infin}a_{j} \, cos \, j \omega t + \sum_{j=1}^{\infin}b_{j} \, sen \, j \omega t }

Força transitória

Excitação caracterizada por uma liberação de energia grande em um intervalo curto de tempo. Inúmeros exemplos descrevem este tipo de força: explosão, impacto, etc

Força aleatória

São forças de excitação que não descrevem um padrão determinístico que possa ser definido por uma equação. Para tratar sistemas excitados por forças aleatórias é necessário utilizar métodos estatísticos. Fenômenos aeroelásticos são exemplos de sistemas excitados por forças aleatórias, como forças em asas de aviões, ventos em colunas de pontes, etc.

Exemplo de função harmônica	Exemplo de função periódica não harmônica	Exemplo de função de força transitória	Exemplo de força aleatória

Análise de vibração

Preparação do satélite OGO-6 para teste de vibração.

Um sistema oscilatório é um sistema cujas variáveis de entrada e de saída dependem do tempo. Analisando portanto, as respostas de um sistema depende das condições iniciais impostas sobre ele. Na prática, os problemas encontrados de vibrações são muito complexos, necessitando de ferramentas computacionais para resolve-los e também ainda assim, fica difícil, detalhar completamente o modelo. Com isso, somente as características mais importantes são consideradas na análise.

Os testes de vibração são realizados pela introdução de uma função de forças em uma estrutura, geralmente com algum tipo de agitador.Em alternativa, um DUT (dispositivo sob teste) está ligado a "mesa" de um agitador. Para frequências relativamente baixas, forçando, são utilizados servo-hidráulicos (electro) agitadores são usados. Para frequências mais altas, são utilizados agitadores eletrodinâmicos. Geralmente um ou mais pontos de controle localizados no lado DUT de um dispositivo elétrico, são mantidos a uma aceleração especificada.Outros pontos "de resposta" apresentam nível máximo de vibração (ressonância) ou nível mínimo de vibração (anti-ressonância). É normalmente preferível ativar anti-ressonância para evitar um sistema de se tornar muito ruidoso, ou para reduzir a tensão em certas partes de um sistema devido a modos de vibração causados por específicas frequência de vibração. Dois tipos típicos de teste de vibração são os testes senoidais aleatórios . Os testes senoidais (uma frequência de cada vez) são realizados para examinar a resposta estrutural do dispositivo sob teste (DUT). Um teste aleatório (todas as frequências de uma só vez) é geralmente considerado para replicar mais de perto um ambiente do mundo real, tais como insumos caminhos para um automóvel em movimento. A maioria dos testes de vibração são conduzidos num único eixo DUT de cada vez, embora a maior vibração do mundo real ocorre em vários eixos simultaneamente. MIL-STD-810G, lançado no final de 2008, Test Method 527, exige testes de excitação múltipla. Dispositivos projetados especificamente para rastrear ou gravar vibrações são chamados vibroscópios.

Sistemas oscilatórios com dois graus de liberdade

Definição

Até aqui foram tratados sistemas com vibratórios em que apenas uma coordenada de deslocamento definia totalmente a vibração. Em termos analíticos, a vibração ficou caracterizada pela solução de uma única equação diferencial do tipo ordinária na variável independente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} . Outra característica importante do que foi visto em sistemas com um grau de liberdade é a existência de uma frequência natural que desempenha uma papel importante tanto na vibração livre quanto na vibração forçada.

A descrição de sistema com dois graus de liberdade implica dizer que são necessárias duas coordenadas independentes para caracterizar o sistema vibratório. Isso implica a existência de duas equações de movimento associado, um para cada massa. De modo geral, essas equações estão na forma de equações diferenciais acopladas, ou seja, cada equação envolve todas as coordenadas.

Modos de vibração

Durante a vibração livre, um sistema com dois graus de liberdade tem dois modos normais de vibração, correspondentes as duas frequências naturais, nas quais as amplitudes dos dois graus de liberdade são relacionadas de modos específicos, denominado modo normal, modo principal ou modo natural de vibração.

Simplificação

A configuração de um sistema com dois graus de liberdade pode ser especificada por um conjunto de coordenadas independentes, denominadas coordenadas generalizadas. Dado que as equações de movimento de um sistema de dois graus de liberdade geralmente são acopladas, de forma que cada equação envolve todos os parâmetros, é sempre possível determinar um conjunto particular de coordenadas de modo que cada equação de movimento contenha apenas uma coordenada. Assim, as equações de movimento se tornam não acopladas e podem ser resolvidas de forma individual. Tal conjunto é denominado coordenadas principais.

Equação de Movimento para Vibrações Forçadas

Se considerarmos um sistema massa-mola com amortecedor viscoso e com dois graus de liberdade como mostra a figura ao lado.

Sistema massa mola e amortecedor com 2 graus de liberdade

O movimento desse sistema será descrito pelas coordenadas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1(t)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2(t)} , que definem as posições das respectivas massas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_2} seja qual for o instante de tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} tendo as posições de equilíbrio como referência. Os respectivos diagramas de corpo livre das massas $m_{1}$e $m_{2}$ podem ser representados conforme o diagrama de corpo livre.

Diagrama de Corpo Livre

Ao aplicarmos a segunda lei de Newton para cada massa teremos:

$F_{1}=m_{1}{\ddot {x_{1}}}+(c_{1}+c_{2}){\dot {x_{1}}}-c_{2}{\dot {x}}+(k_{1}+k_{2})x_{1}-k_{2}x_{2}\mathrm {\textvisiblespace} (1)$

$F_{2}=m_{2}{\ddot {x_{2}}}-c_{2}{\dot {x_{1}}}+(c_{2}+c_{3}){\dot {x_{2}}}-k_{2}x_{1}+(k_{2}+k_{3})x_{2}\mathrm {\textvisiblespace} (2)$

Pode-se perceber que a equação $(1)$ possui termos que envolvem $x_{2}$ e que a equação $(2)$ também possuirá termos que envolvam $x_{1}$. O significado disso é que essas equações representam um sistema de duas EDOs de segunda ordem interligadas. Dessa forma devemos esperar que o movimento de $m_{1}$ exerça influência em $x_{2}$ e que o movimento de $m_{2}$ também influencie no movimento de $m_{1}$. As equações $(1)$ e $(2)$ podem ser escritas matricialmente da forma:

${\overrightarrow {F}}(t)=[m]{\overrightarrow {\ddot {x}}}(t)+[c]{\overrightarrow {\dot {x}}}(t)+[k]{\overrightarrow {x}}$

sendo que $[m]$, $[c]$ e $[k]$ são chamadas respectivamente de matriz de massa, amortecimento e rigidez

$[m]={\begin{bmatrix}m_{1}&0\\0&m_{2}\end{bmatrix}}$

$[c]={\begin{bmatrix}c_{1}+c_{2}&-c_{2}\\-c_{2}&c_{2}+c_{3}\end{bmatrix}}$

$[k]={\begin{bmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{2}+k_{3}\end{bmatrix}}$

${\overrightarrow {x}}(t)$ e ${\overrightarrow {F}}(t)$ são denominados os vetores de deslocamento e força, são representados por:

${\overrightarrow {x}}(t)={\begin{Bmatrix}x_{1}(t)\\x_{2}(t)\end{Bmatrix}}$

e

${\overrightarrow {F}}(t)={\begin{Bmatrix}F_{1}(t)\\F_{2}(t)\end{Bmatrix}}$

Pode-se perceber que as matrizes $[m]$, $[c]$ e $[k]$ matrizes quadradas de ordem 2 e que seus elementos são respectivamente, as massas, os coeficientes de amortecimento e as constantes de rigidez das molas ilustrados no problema. Também podemos afirmar que as matrizes são simétricas, e que suas transpostas são iguais as próprias matrizes

$[m]^{T}=[m]$

$[c]^{T}=[c]$

$[k]^{T}=[k]$

Pode-se observar que as equações $(1)$ e $(2)$ deixam de ser independentes apenas quando $c_{2}=k_{2}=0$ que implicaria que as massas $m_{1}$ e $m_{2}$ não estão conectadas. Para esse caso, as matrizes $[m]$, $[c]$ e $[k]$ passam a ser diagonais. A solução das equações $(1)$ e $(2)$ envolve quatro constantes de integração, sendo duas para cada equação.

Normalmente, os deslocamentos e as velocidades iniciais das duas massas são tomados como:

$x_{1}(t=0)=x_{1}(0)$

${\dot {x_{1}}}(t=0)={\dot {x_{1}}}(0)$

${x_{2}}(t=0)=x_{2}(0)$

${\dot {x_{2}}}(t=0)={\dot {x_{2}}}(0)$

Determinação das frequências naturais e dos modos de vibração

Primeiramente é necessário determinar as frequências naturais do sistema. Assumindo que a solução é da forma

${\textbf {x}}(t)={\textbf {u}}e^{j\omega t}$

em que ${\textbf {u}}$ é um vetor de constante a se determinar, $\omega$ é a frequência natural que queremos determinar e $j={\sqrt {-1}}$. Temos que $e^{j\omega t}$ representa um movimento harmônico desde que $e^{j\omega t}=cos\,\omega t+j\,sen\,\omega t$. Dessa forma, substituindo ${\textbf {x}}(t)$ na equação de movimento do sistema encontramos

$(-\omega ^{2}M+K){\textbf {u}}e^{j\omega t}={\textbf {0}}$

em que $M$ e $K$ são as matrizes de massa e de rigidez respectivamente. Podemos dividir os dois lados da equação por $e^{j\omega t}$ uma vez que o termo $e^{j\omega t}\neq 0$ para qualquer valor de $t$. Obtemos assim a equação

$(-M\omega ^{2}+K){\textbf {u}}={\textbf {0}}$

Para que a equação acima possua uma solução não trivial temos que a matriz $(-M\omega ^{2}+K)$ deve ser singular e portanto

$det{\begin{bmatrix}-\omega ^{2}m_{1}+k_{1}+k_{2}&-k_{2}\\-k_{2}&-\omega ^{2}m_{2}+k_{2}\end{bmatrix}}=0$

calculando o determinante acima encontramos a seguinte equação

$m_{1}m_{2}\omega ^{4}-(m_{1}k_{2}+m_{2}k_{1}+m_{2}k_{2})\omega ^{2}+k_{1}k_{2}=0$

se considerarmos que a variável é $\omega ^{2}$ teremos uma equação de segundo grau e que apresenta duas raízes $\omega _{1}^{2}$ e $\omega _{2}^{2}$ que são as frequências naturais do sistema.

Uma vez obtido as frequências naturais pode-se resolver as equações abaixo a fim de encontrar os modos de vibração ${\textbf {u}}_{1}$e ${\textbf {u}}_{2}$

$(-\omega _{1}^{2}M+K){\textbf {u}}_{1}={\textbf {0}}$

$(-\omega _{2}^{2}M+K){\textbf {u}}_{2}={\textbf {0}}$

Sistemas oscilatórios com vários graus de liberdade

Definição

A partir de agora serão considerados sistemas vibratórios com mais de dois graus de liberdade. É uma extensão da exposição para sistemas caracterizados por mais de duas coordenadas generalizadas. A vibração será definida pela solução de um sistema de equações diferenciais ordinárias na variável independente $t$. Em geral, será conveniente a utilização de matrizes para o tratamento do problema.

O conceito de graus de liberdade está associado aos possíveis deslocamentos que um conjunto de corpos acoplados pode realizar no espaço físico. Assim, um ponto material totalmente livre pode efetuar deslocamentos nas três direções do espaço; tem, portanto, três graus de liberdade, que coincidem com o número de coordenadas necessárias para definir um deslocamento finito do ponto.

Chamam-se de vínculos as restrições impostas ao deslocamento dos corpos móveis. Os vínculos sempre diminuem os graus de liberdade. Assim, se o deslocamento do ponto for restrito a um plano, o número de graus de liberdade passará a ser dois e, se for restrito a uma reta, terá apenas um grau de liberdade. É evidente que, se o ponto material por ação vincular não puder sofrer deslocamentos, então não terá nenhum grau de liberdade.

Sistemas mecânicos em sua maioria podem ter um número infinito de graus de liberdade. Para cada grau de liberdade existe uma única equação de movimento, sendo cada equação obtida por meio da segunda lei de movimento de Newton, no entanto se torna mais conveniente deduzir as equações de movimento de um sistema com muitos graus de liberdade utilizando equações de Lagrange. Além disso, cada equação pode ser considerada acoplada, ou seja, cada uma envolve mais que uma coordenada, significando que estas não podem ser resolvidas individualmente, apenas simultaneamente.

Tendo um sistema com n graus de liberdade, obtém-se n frequência naturais, cada uma associada a sua própria forma modal. Além disso a medida que o número de graus de liberdade aumenta, a solução da equação característica se torna mais complexa. Para calcular o número de graus de liberdade, pode-se utilizar o seguinte método:

$$Numero\ \ de\ \ graus\ \ de\ \ liberdade=Numero\ \ de\ \ massas\ \ no\ \ sistema\ \times \ Numero\ \ de\ \ tipos\ \ de\ \ movimentos\ \ possiveis\ \ de\ \ cada\ \ massa$$

Modelagem

Adota-se métodos para aproximar um sistema contínuo em um sistema com vários graus de liberdade, dos quais, dois são listados a seguir:

• Sistema de massa concentrada: consiste em substituir a massa ou inércia distribuída por um número finito de massas concentradas ou corpos rígidos. Tais massas estão ligadas por elementos elásticos e amortecedores, ambos de massa desprezível. Nota-se que quanto maior o número de massas concentradas, maior será a precisão da análise, pois assim ocorre maior aproximação do real.
• Método do elemento finito: envolve substituir a geometria do sistema por um grande número de elementos infinitesimais, onde novamente, quanto maior o número de elementos, maior a precisão.

Equação de movimento

Aplicando a segunda lei do movimento de Newton para um sistema massa-mola-amortecedor com n graus de liberdade obtém-se a seguinte equação de movimento:

$$\left[m\right]{\ddot {\overrightarrow {x}}}+\left[c\right]{\dot {\overrightarrow {x}}}+\left[k\right]{\overrightarrow {x}}={\overrightarrow {F}}$$

Onde $\left[m\right],\ \left[c\right]$ e $\left[k\right]$ são denominados de matrizes de massa, amortecimento e rigidez, respectivamente. Tais matrizes são dadas por:

$$\mathbf {[m]} ={\begin{bmatrix}m_{11}&m_{12}&\cdots &m_{1n}\\m_{21}&m_{22}&\cdots &m_{2n}\\\vdots &\vdots &\ddots &\vdots \\m_{n1}&m_{n2}&\cdots &m_{nn}\end{bmatrix}}\qquad {\mathbf {[c]} ={\begin{bmatrix}c_{11}&c_{12}&\cdots &c_{1n}\\c_{21}&c_{22}&\cdots &c_{2n}\\\vdots &\vdots &\ddots &\vdots \\c_{n1}&c_{n2}&\cdots &c_{nn}\end{bmatrix}}}\qquad {\mathbf {[k]} ={\begin{bmatrix}k_{11}&k_{12}&\cdots &k_{1n}\\k_{21}&k_{22}&\cdots &k_{2n}\\\vdots &\vdots &\ddots &\vdots \\k_{n1}&k_{n2}&\cdots &k_{nn}\end{bmatrix}}}$$

Se a matriz de rigidez tem no mínimo um termo não nulo fora da sua diagonal, diz-se que o sistema está estaticamente acoplado. Caso esta situação ocorra na matriz de massa, tem-se que o sistema é dinamicamente acoplado. Se ambas as matrizes de massa e de rigidez tiverem termos não-zero fora da diagonal, o sistema é acoplado estática e dinamicamente.

Além disso ${\ddot {\overrightarrow {x}}},\ {\dot {\overrightarrow {x}}},\ {\overrightarrow {x}}$ e ${\overrightarrow {F}}$ são os vetores aceleração, velocidade, deslocamento e força respectivamente, que atuam no sistema a ser analisado, e estes são dados por:

$${\overrightarrow {x}}={\begin{Bmatrix}x_{1}(t)\\x_{2}(t)\\.\\.\\.\\x_{n}(t)\end{Bmatrix}}\qquad {\dot {\overrightarrow {x}}}={\begin{Bmatrix}{\dot {x}}_{1}(t)\\{\dot {x}}_{2}(t)\\.\\.\\.\\{\dot {x}}_{n}(t)\end{Bmatrix}}\qquad {\ddot {\overrightarrow {x}}}={\begin{Bmatrix}{\ddot {x}}_{1}(t)\\{\ddot {x}}_{2}(t)\\.\\.\\.\\{\ddot {x}}_{n}(t)\end{Bmatrix}}\qquad {\overrightarrow {F}}={\begin{Bmatrix}F_{1}(t)\\F_{2}(t)\\.\\.\\.\\F_{n}(t)\end{Bmatrix}}$$

Ver também

• Vibração longitudinal
• Vibração flexional
• Vibração torcional