Calor específico

Calor específico é uma grandeza física intensiva que define a variação térmica de determinada substância ao receber determinada quantidade de calor. Também é chamado de capacidade térmica mássica. A unidade no SI é J/(kg.K) (joule por quilograma e por kelvin). Uma unidade usual bastante utilizada para calores específicos é cal/(g °C) (caloria por grama e por grau Celsius).

Em rigor há dois calores específicos distintos: o calor específico a volume constante $c_{v}$ e o calor específico a pressão constante $c_{p}$. O calor específico a pressão constante é geralmente um pouco maior do que o calor específico a volume constante, sendo a afirmação verdadeira para materiais com coeficientes de dilatação volumétrico positivos. Em virtude do aumento de volume associado à dilatação térmica, parte da energia fornecida na forma de calor é usada para realizar trabalho contra o ambiente a pressão constante e não para aumentar a temperatura em si; o aumento de temperatura experimentado para um sistema à pressão constante é pois menor do que aquele que seria experimentado pelo mesmo sistema imposto o volume constante uma vez mantida a mesma transferência de energia na forma de calor. No caso do calor específico a volume constante, toda a energia recebida na forma de calor é utilizada para elevar a temperatura do sistema, o que faz com que $c_{v}$ — em virtude de sua definição — seja um pouco menor. A diferença entre os dois é particularmente importante em gases; em sólidos e líquidos sujeitos a pequenas variações de volume frente às variações de temperatura, os valores dos dois na maioria das vezes se confundem por aproximação. Em análise teórica e de precisão, contudo, é importante a diferenciação dos dois.

Materiais com dilatação anômala, como a água entre 0 °C e 4 °C, não obedecem à regra anterior; nestes casos o calor específico a volume constante é então um pouco maior do que o calor específico a pressão constante.

Definição

O calor específico ($c\,\!$) de uma substância pode ser definido a partir da capacidade térmica ($C\,\!$) de um corpo composto por ela como o quociente desta pela massa ($m\,\!$) desse corpo. Matematicamente,

$c={\frac {C}{m}}\,\!$

A capacidade térmica, por sua vez, é definida como a razão entre calor recebido e variação de temperatura observada. Assim, o calor específico pode ser expresso como:

$c={\frac {1}{m}}{\frac {\delta Q}{\delta T}}$

Por essa última relação, nota-se que o calor específico depende do processo pelo qual o calor é cedido à substância. Usando a primeira lei da termodinâmica, com $p$ sendo a pressão, pode-se escrever:

$c={\frac {1}{m}}{\frac {\mathrm {d} U+p\mathrm {d} V}{\mathrm {d} T}}$

Dois casos particulares são de maior importância. Um deles é o calor específico a volume constante, onde o termo representando o trabalho ($p\mathrm {d} V$) é nulo, e pela relação anterior

$c_{v}={\frac {1}{m}}{\frac {\mathrm {d} U}{\mathrm {d} T}}$

O segundo caso é o calor específico a pressão constante. Nesse caso, a equação anterior resulta em

$c_{p}={\frac {1}{m}}{\frac {\mathrm {d} \left(U+pV\right)}{\mathrm {d} T}}$,

onde a nova função de estado $H=U+pV$ é entalpia do sistema.

A distinção entre esses dois calores específicos pode normalmente ser ignorada nas fases sólida e líquida, dado que essas substâncias normalmente sofrem uma variação de volume muito pequena. Gases, no entanto, apresentam grande expansão térmica, sendo sempre necessária a distinção entre ambos os calores específicos.

Calor específico molar

Em muitas circunstâncias a unidade mais conveniente para especificar a quantidade de uma substancia é o mol, definido como sendo uma quantidade de 6,02 x 10²³ unidades elementares de qualquer substância. Assim, por exemplo um mol de alumínio significa 6,02 x 10²³ átomos de alumínio (o átomo é a unidade elementar), e 1 mol de óxido de alumínio significa 6,02 x 10²³ fórmulas moleculares do composto.

Nesses casos, quando a quantidade de substância é expressa em moles, utiliza-se o chamado calor específico molar, que é expresso como sendo a capacidade térmica por mol. De forma análoga com o calor específico por massa, o calor específico molar depende do processo ao qual a substância é submetida; define-se de mesma forma as quantidades a pressão constante e a volume constante.

Calor específico molar a volume constante

O calor específico molar a volume constante é definido como:

$c_{v}={\frac {Q}{n\Delta T}}={\frac {\Delta U}{n\Delta T}}$

Sendo que,

$\Delta U=Q-W$ (primeira lei da termodinâmica) com o trabalho $W=0$ temos $\Delta U=Q$,por se tratar de um processo a volume constante.

onde:

• $Q$ é o calor absorvido ou cedido por uma amostra de $n$ moles de um gás;
• $\Delta T$ é a variação de temperatura resultante;
• $\Delta U$ é a variação de energia interna.

Para um gás monoatômico ideal,

$c_{v}={\frac {3}{2}}R=12,5J/mol/K$

Calor específico molar a pressão constante

O calor específico molar a pressão constante é definido como:

$c_{p}={\frac {Q}{n\Delta T}}$

Sendo que temos as seguintes relações:

$Q=U+W$ (primeira lei da termodinâmica) e $W=p\Delta V$. Relacionando o trabalho com a equação dos gases ideais $pV=nRT$ ficamos com $W=nR\Delta T$. Substituindo a as respectivas equações mais a equação $c_{v}={\frac {\Delta U}{n\Delta T}}$ na equação $Q=U+W$ ficamos com

$c_{p}=c_{v}+R$

onde:

• $Q$ é o calor absorvido ou cedido por uma amostra de $n$ mols de um gás;
• $\Delta T$ é a variação de temperatura resultante;
• $\Delta U$ é a variação de energia interna.

Regra de Dulong-Petit

A regra de Dulong-Petit consiste em obter, aproximadamente, o calor específico das substâncias por meio da massa molar:

$c\cong {\frac {3R}{M}}$

Em que:

• $c$ é o calor específico, em joule por quilograma kelvin (J.kg⁻¹.K⁻¹);
• $R$ é a constante dos gases reais, equivalente a 8,31 joules por mol kelvin (J.K⁻¹.mol⁻¹);
• $M$ é a massa molar, em quilograma por mol (kg/mol).

Unidades

Sistema internacional

A unidade SI para calor específico é joule por kelvin por quilograma (J / K / kg, J / (kg K), JK ^-1 kg ^-1 , etc.). Como um incremento de temperatura de um grau Celsius é o mesmo que um incremento de um kelvin, é o mesmo que joule por grau Celsius por quilograma (J / ° C / kg). Às vezes, o grama é usado em vez de quilograma para a unidade de massa: 1 J / K / kg = 0,001 J / K / g.

O calor específico de uma substância (por unidade de massa) tem dimensão L ² · T − ² · Θ ⁻¹ ou (L / T) ² / Θ. Portanto, a unidade SI J / K / kg é equivalente ao metro quadrado por segundo ao quadrado por kelvin (m ² K ⁻¹ s ⁻² ).

Unidades de engenharia inglesas (imperiais)

Profissionais da construção , engenharia civil , engenharia química e outras disciplinas técnicas, especialmente no Estados Unidos , pode utilizar os chamados unidades de Inglês Engenharia , que incluem a imperial libra (lb = 0,45459237 kg) como unidade de massa, o grau Fahrenheit ou Rankine (° F = 5/9 K, cerca de 0,555556 K) como a unidade de incremento de temperatura, e a unidade térmica britânica (BTU ≈ 1055.06 J),  como a unidade de calor.

Medição do calor específico de uma substância

Calorímetro

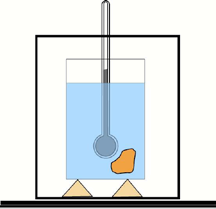
A capacidade calorífica de um corpo é determinada com ajuda de um calorímetro e um termômetro. Um calorímetro simples (veja a figura) consiste num cilindro metálico polido, colocado num outro cilindro metálico sobre cortiça (para isolamento térmico).

O calor específico de uma substância é normalmente determinado de acordo com a definição; ou seja, medindo a capacidade térmica de uma amostra da substância, geralmente com um calorímetro , e dividindo pela massa da amostra. Várias técnicas podem ser aplicadas para estimar a capacidade térmica de uma substância como, por exemplo, calorimetria de varredura diferencial rápida .

O cilindro interno é enchido com água ou algum outro líquido de calor específico conhecido. Um corpo de massa m, e capacidade calorífica específica c, aquecido a uma certa temperatura T é imergido no calorímetro de massa m₁ e capacidade calorífica c₁ na qual a temperatura é medida. Suponha que a temperatura deste líquido de m₂ e capacidade calorífica específica c₂ no calorímetro é T’ antes de o corpo ser emergido nele, e quando a temperatura do líquido e do corpo é a mesma, a temperatura torna-se T_f.

Da lei de conservação da energia e considerando o calor dissipado na vizinhança pelo objecto quente Q, o calor recebido pela água e pelo calorímetro que seja respectivamente Q₁ e Q₂ , mostra que a capacidade calorífica específica é

$c={\frac {c_{1}m_{1}(T_{f}-T)+c_{2}m_{2}(T_{f}-T')}{m(T-T_{f})}}={\frac {(c_{1}m_{1}+c_{2}m_{2})(T_{f}-T')}{m(T-T_{f})}}$

Fatores que afetam o calor específico

Representação de uma molécula vibrando.

Moléculas sofrem muitas vibrações características internas. A energia potencial armazenada nestes graus de liberdade internos contribui para uma amostra do conteúdo de energia, mas não a sua temperatura. Graus de liberdade mais internos tendem a aumentar a capacidade de uma substância de calor específico, contanto que as temperaturas são suficientemente elevadas para superar os efeitos quânticos.

Graus de liberdade

O comportamento termodinâmico das moléculas dos gases monoatômicos, como hélio, e dos gases diatômicos, como o nitrogênio, é muito diferente. Em gases monoatômicos, a energia interna é unicamente para movimentos de translação. Os movimentos são movimentos de translação em um espaço tridimensional em que as partículas se movem e trocam energia em colisões elásticas da mesma forma como fariam bolas de borracha colocadas num recipiente que foi agitado fortemente. (Veja animação aqui). Estes movimentos nas dimensões X, Y, e Z significam que os gases monoatômicos tem apenas três graus de liberdade de translação. Moléculas com maior atomicidade, no entanto, tem vários graus de liberdade interna, rotacionais e vibracionais. Elas se comportam como uma população de átomos que podem se mover dentro de uma molécula de formas diferentes (veja a animação à direita). A energia interna é armazenada nesses movimentos internos. Por exemplo, o nitrogênio, que é uma molécula diatômica, tem cinco graus de liberdade: três de translação e dois de rotação interna. Note que a calor específico molar a volume constante do gás monoatômico é ${\frac {3}{2}}R$, sendo R a constante universal do gás ideal, ao passo que para o valor do nitrogênio (diatômico) vale ${\frac {5}{2}}$, o que mostra claramente a relação entre os graus de liberdade e ao calor específico.

$c_{v}=({\frac {f}{2}})R$ onde $f$ é o número de graus de liberdade.

Massa molar

Uma razão pela qual o calor específico tem valores diferentes para diferentes substâncias é a diferença de massas molares, que é a massa de um mol de qualquer elemento, que é diretamente proporcional à massa molecular do elemento, a soma dos valores das massas atômicas da molécula em questão. A energia térmica é armazenada pela existência de átomos ou moléculas de vibração. Se uma substância tem uma massa molar mais leve, em seguida, cada grama de que tem mais átomos ou moléculas disponíveis para armazenar energia. Esta é a razão pela qual o hidrogênio, a substância com menor massa molar tem um calor específico muito elevado. A consequência deste fenômeno é a de que, quando se mede o calor específico em termos molares a diferença entre substâncias torna-se menos acentuada e o calor específico de hidrogênio para de ser atípico. Da mesma forma, as substâncias moleculares (também absorvem calor em seus graus de liberdade internos) pode armazenar grandes quantidades de energia por mol se é moléculas grandes e complexas, e, portanto, seu calor específico medido em massa é menos perceptível . Uma vez que a densidade média de um elemento químico está fortemente relacionada com a sua massa molar, em termos gerais, há uma forte correlação inversa entre a densidade do sólido e o $c_{p}$ (calor específico a pressão constante). Lingotes sólidos grandes de baixa densidade tendem a absorver mais calor do que um lingote pequeno de mesma massa, porém com densidade mais elevada que o primeiro, porque contém mais átomos. Por conseguinte, em termos gerais, há uma forte correlação entre o volume de um elemento sólido e a sua capacidade total de calor. No entanto, existem muitos desvios desta correlação.

As ligações de hidrogênio

Contendo hidrogênio na sua composição, moléculas polares como o etanol, amônia e água, têm poderosas ligações intermoleculares de hidrogênio quando em sua fase líquida. Estas ligações proporcionam um outro local em que o calor pode ser armazenado como energia potencial de vibração, mesmo em baixas temperaturas comparativamente.

Impurezas

No caso de ligas, existem certas condições em que as pequenas impurezas podem alterar grandemente o calor específico medido. As ligas podem mostrar uma diferença marcada no seu comportamento, mesmo que a impureza em questão seja um dos elementos que formam a liga, tais como ligas impuras em semicondutores ferromagnéticos que podem conduzir a medições muito diferentes.

A tabela abaixo apresenta o calor específico de algumas substâncias à pressão constante de 1 atm.

Substância	Calor Específico (cal/g.°C)
água	1,0
álcool	0,58
alumínio	0,22
ar	0,24
carbono	0,12
chumbo	0,031
cobre	0,094
ferro	0,11
gelo	0,5
hélio	1,25
hidrogênio	3,4
latão	0,092
madeira	0,42
mercúrio	0,033
nitrogênio	0,25
ouro	0,032
oxigênio	0,22
prata	0,056
rochas	0,21
vidro	0,16
zinco	0,093

Ver também

• Wikilivros

• Calorimetria
• Calor latente

Referências

Bibliografia

• HALLIDAY, D., RESNICK,R., WALKER, J., Fundamentos de física. 8ª edição, vol. 2, editora LTC