Exame de Graham

O Exame de Graham, cuja denominação vem de Ronald Graham, é uma técnica de computação usada para determinar o envoltória convexa de um dado conjunto de pontos no plano como complexidade de tempo O(n log n).

O Algoritmo

Ilustração

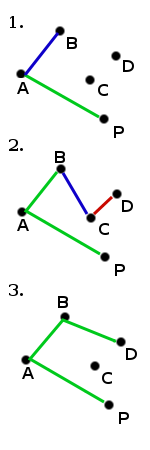
Como se pode notar, A para B e B para C são no sentido horário, mas C de D não é. Este algoritmo detecta esta situação e descarta segmentos escolhidos anteriormente até que se orientem no sentido horário (B para D neste caso.)

O primeiro passo neste algoritmo é encontrar o ponto com a menor coordenada y. Se houver um empate, o ponto com menor coordenada x deve servir como critério de desempate. Chamaremos esta ponto de P . Este passo é da ordem O (n), onde n é o número de pontos em questão.

Depois, o conjunto de pontos deve ser ordenado em ordem crescente do ângulo que ele com o ponto P formam com o eixo X. Qualquer algoritmo ordenação de uso geral é apropriado para isto, por exemplo, o heapsort (o qual é da ordem de O(n log n)). De forma a acelerar os cálculos, não é necessário calcular os ângulos que estes pontos formam com o eixo x; ao invés disto é suficiente calcular a tangente deste ângulo, que pode ser feito com simples aritmética.

O algoritmo procede considerando cada um dos pontos do array ordenado em sequência. Para cada ponto, é determinado, se ao mover-se dos dois pontos anteriores para este ponto se forma uma "curva para esquerda" ou uma "curva para direita". Se é uma "curva para esquerda", isto significa que o ponto de partida não faz parte do envoltório convexo e deve ser removido da pesquisa. Este processo continua ao longo do conjunto até que o conjunto dos três últimos pontos seja uma curva para direita. Assim que uma "curva para esquerda" é encontrada, o algoritmo salta para o próximo ponto do array ordenado. ( Se em qualquer etapa três pontos são colineares, é indiferente se o ponto do meio é removido ou não. Removendo-o obteremos um envoltório convexo mínimo, mas o mantendo isto não o inválida).

Novamente, para determinar se três pontos constituem uma "curva a esquerda" ou "curva a direita" não é necessário calcular o ângulo existente entre os dois segmentos de retas, isto pode ser obtido simplesmente por aritmética inteira. Dado três pontos $(x_{1},y_{1})$, $(x_{2},y_{2})$ e $(x_{3},y_{3})$, simplesmente calculando o produto vetorial $(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})$ dos dois vetores definidos pelos pontos $(x_{1},y_{1})$, $(x_{2},y_{2})$ e $(x_{2},y_{2})$, $(x_{3},y_{3})$. Se o resultado for Zero, os três pontos são colineares, se for positivo, os três pontos constituem uma "curva para esquerda", caso contrário uma "curva para direita".

Este processo irá eventualmente retornar ao ponto de início, neste ponto o algoritmo estará concluído e o array agora contém os pontos do envoltório convexo no sentido anti-horário.

Pseudocódigo

Este algoritmo resultará no envoltório convexo mínimo. O resultado estará armazenado na Pilha.

 Find pivot P;
 Sort Points by angle (resolve ties in favor of point farther from P);

# Points[1] is the pivot
 Stack.push(Points[1]);
 Stack.push(Points[2]);
 FOR i = 3 TO Points.length
         o <- Cross_product(Stack.second, Stack.top, Points[i]);
         IF o == 0 THEN
                 Stack.pop;
                 Stack.push(Points[i]);
         ELSEIF o > 0 THEN
                 Stack.push(Points[i]);
         ELSE
                 WHILE o <= 0 and Stack.length > 2
                         Stack.pop;
                         o <- Cross_product(Stack.second, Stack.top, Points[i]);
                 ENDWHILE
                 Stack.push(Points[i]);
         ENDIF
 NEXT i

 FUNCTION Cross_product(p1, p2, p3)
         RETURN (p2.x - p1.x)*(p3.y - p1.y) - (p3.x - p1.x)*(p2.y - p1.y);
 ENDFUNCTION

Referências

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Pages 949–955 of section 33.3: Finding the convex hull.

Ligações externas

• «C++ and Object Pascal Graham Scan Implementations»