Efeito de Eötvös

Predefinição:Sem notas No início do século XX, uma equipe do Instituto de Geodesia de Potsdam efetuou uma experiência baseada em medições de gravidade em navios em movimento nos oceanos Atlântico, Índico e Pacífico. Enquanto estudava os resultados desta experiência, o nobre e físico húngaro Loránd Eötvös (1848-1919) verificou que as medições eram menores quando o navio se movia para oriente e maiores quando se movia para ocidente. Ele identificou este fenômeno como consequência principal da rotação da Terra. Em 1908 foram efectuadas novas medições no Mar Negro com dois navios, um movendo-se para oriente e outro para ocidente. Os resultados provaram a teoria de Eötvös. Desde então que os geodesistas usam a seguinte fórmula para corrigir a velocidade relativa da Terra durante uma medição gravimétrica.

$a_{r}=2\Omega u\cos \phi +{\frac {u^{2}+v^{2}}{R}}.$

Onde:

$\Omega$ - rotação da Terra

$u$ - velocidade na direcção latitudinal (Este-Oeste)

$\phi$ - latitude do lugar do observador

$v$ - velocidade na direcção longitudinal (Norte-Sul)

$R$ - raio da Terra

O primeiro termo na fórmula, 2Ωucos(φ), corresponde ao efeito de Eötvös. O segundo termo é uma refinação que em circunstancias normais é muito menor que o efeito de Eötvös.

Explicação Física

O efeito de Eötvös varia quanto maior for a força ascendente a ser introduzida para manter um corpo em flutuação neutral.

Movimento ao longo do equador

Dando atenção à flutuação, será usado um exemplo com balões ou dirigíveis. Temos um dirigível com uma massa de 10 toneladas, com uma velocidade de cruzeiro de 25 metros por segundo (90 km/h).

Para calcular o quanto o dirigível necessita para flutuar neutralmente quando está estacionário relativamente à Terra, há que ter em conta o facto ter um movimento de rotação. Sobre o equador, a velocidade da superfície da Terra é de cerca de 465 metros por segundo. A quantidade de força centrípeta necessária para causar o movimento de uma massa ao longo de um caminho circular de raio de 6378 quilómetros (o raio equatorial da Terra) a 465 m/s, é de cerca de 0,034 newtons por cada quilograma de massa. Para o dirigível de 10 toneladas, essa quantidade é de cerca 340 newtons. A quantidade de força de flutuação necessária corresponde então à massa do dirigível (multiplicado pela aceleração da gravidade), menos aqueles 340 newtons. Por outras palavras, qualquer objecto que se mova solidariamente com a Terra sobre o equador tem o seu peso reduzido em 0,34%, graças à rotação da Terra.

Quando circula a 25m/s para oriente, a velocidade total torna-se 465 + 25 = 490m/s, o que requer uma força centrípeta de cerca de 375 newtons. Circulando a 25m/s para ocidente, a velocidade total é 465 - 25 = 440 m/s, necessitando de 305 newtons. Assim, se o dirigível estiver em flutuação neutra enquanto circula para oriente, não continuará a estar em flutuação neutra após uma inversão de marcha. Após a inversão de marcha, o peso de 10 toneladas (10.000 kg) terá um acréscimo de 7 quilogramas, e o dirigível terá de ser compensado para manter o equilíbrio. Por outro lado, num planeta sem rotação, ao efetuar a mesma inversão de marcha não seria necessário uma compensação por parte do condutor para manter a flutuação neutra.

Em meteorologia, há que ter em conta este efeito em modelos de alta precisão. As massas de ar que têm uma velocidade relativamente à Terra têm tendência a migrar para outra altitude, pelo que este efeito tem de ser considerado.

Dedução da fórmula para um caso simplificado

Dedução da fórmula para o movimento ao longo do equador.

Um sistema de coordenadas conveniente nesta situação é o sistema de coordenadas inercial que se move solidário ao centro de massa da Terra. Então é válido o seguinte: os objectos que estejam em repouso na superfície da Terra, com rotação solidária com a Terra, estão a circular em torno do eixo da Terra, pelo que possuem uma força centrípeta respeitante ao sistema de coordenadas inercial.

O que se procura é a diferença entre a aceleração centrípeta do dirigível estando estacionário relativamente à Terra e tendo velocidade respectivamente à Terra.

Notação:

$a_{u}$ - aceleração centrípeta total quando se move ao longo da superfície da Terra.

$a_{s}$ - aceleração centrípeta quando está estacionário respectivamente à Terra.

$\Omega$ - velocidade angular da Terra: uma revolução por dia Sideral.

$\omega _{r}$ - velocidade angular da massa relativamente à velocidade angular da Terra.

$(\Omega +\omega _{r})$ - velocidade angular total da massa.

$\omega _{r}*R=u$ - velocidade da massa relativamente à Terra.

$R$ - raio da Terra.

${\begin{aligned}a_{r}&=a_{u}-a_{s}\\&=(\Omega +\omega _{r})^{2}R-\Omega ^{2}R\\&=\Omega ^{2}R+2\Omega \omega _{r}R+\omega _{r}^{2}R-\Omega ^{2}R\\&=2\Omega \omega _{r}R+\omega _{r}^{2}R\\&=2\Omega u+u^{2}/R\\\end{aligned}}$

Pode verificar-se facilmente que no caso de movimento ao longo do equador, a fórmula para qualquer latitude simplifica na fórmula anterior:

$a_{r}=2\Omega u\cos \phi +{\frac {u^{2}+v^{2}}{R}}$

O segundo termo representa a aceleração centrípeta necessária para que o dirigível siga a curvatura da Terra. É independente quer da rotação da Terra quer da direcção do movimento. Por exemplo, quando um dirigível que efetue instrumentos de medição gravimétrica circule sobre um dos pólos a altitude constante, a trajectória do veículo seguirá a curvatura da Terra. O primeiro termo na fórmula é então zero, devido ao cosseno ser zero quando o ângulo (neste caso a latitude no pólo) é 90º, e o segundo termo representa então a aceleração centrípeta para seguir a curvatura da Terra.

Explicação

A força da gravidade e a força normal. A força resultante age como a força centrípeta necessária.

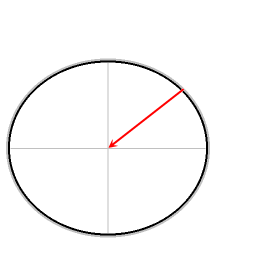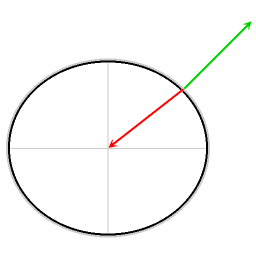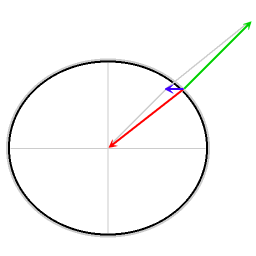
A dedução matemática do efeito de Eötvös para o movimento ao longo do equador explica o factor 2 no primeiro termo da fórmula de correcção de Eötvös.

Devido a esta rotação, a Terra não tem uma forma esférica, sendo achatada nos pólos e alargada no equador. O vector da força da gravidade está dirigida para o centro da Terra. A força normal é perpendicular à superfície local.

Nos pólos e no equador, a força da gravidade e a força normal têm o mesmo módulo mesma direcção e sentidos opostos. A qualquer outra latitude intermédia essas forças não têm a mesma direcção, pelo que há uma força resultante que aponta para o eixo da Terra. A qualquer latitude existe uma quantidade precisa de força centrípeta que é necessária para manter uma espessura regular da camada atmosférica.

Novamente o exemplo do dirigível é conveniente para explicar as forças aplicadas. Quando o dirigível tem uma velocidade relativa à Terra na direcção latitudinal então o peso do veículo não é o mesmo de quando está estacionário relativamente à Terra.

Se o dirigível tiver um movimento no sentido Oeste-Este, então terá tendência a um aumento de velocidade, representando uma diminuição do peso, comparado com o peso que teria numa situação estacionária relativamente à Terra.

Se o dirigível tiver um movimento no sentido Este-Oeste, então terá tendência a perder velocidade, representando um aumento do peso.

O primeiro termo do efeito de Eötvös é proporcional à componente da força centrípeta necessária perpendicular à superfície local da Terra, e é assim descrita por uma lei do cosseno: quanto mais próximo do equador, mais forte é o efeito.

Movimento ao longo de uma latitude de 60 graus

O efeito de Eötvös para um objecto em movimento para leste ao longo de uma latitude de 60º. O objecto tende a afastar-se do eixo da Terra.

O efeito de Eötvös para um objecto em movimento para oeste ao longo de uma latitude de 60º. O objecto tende a aproximar-se do eixo da Terra.

Um objecto localizado a 60º de latitude, movendo-se solidário com a Terra, percorre uma trajectória circular, com um raio de cerca de 3190 km e uma velocidade de cerca 233m/s.

Essa trajetória circular requer uma força centrípeta de cerca de 0,017 newtons para cara quilograma de massa, 170 newtons para um dirigível de 10.000 kg. Para calcular o efeito de Eötvös a uma latitude de 60º de latitude, a componente que é perpendicular à superfície local (vertical local) é tomada, o que aos 60º de latitude é metade da força total. Assim, a essa latitude, qualquer objecto movendo-se solidário à Terra tem o seu peso reduzido em 0,08% graças à rotação da Terra.

Quando o dirigível circula a 25m/s para oriente, a velocidade total torna-se 233 + 25 = 258, o que requer uma força centrípeta de cerca de 208 newtons e uma componente vertical local de cerca de 104 newtons. Circulando a 25m/s para ocidente, a velocidade total torna-se 233-25 = 208m/s, o que requer quer uma força centrípeta de cerca 135 newtons e uma componente vertical local de cerca de 68 newtons. Assim, após fazer uma inversão de marcha o dirigível terá de ser reequilibrado pelo condutor, devido à diferença de 4 quilogramas necessárias para a nova força de flutuação neutra.

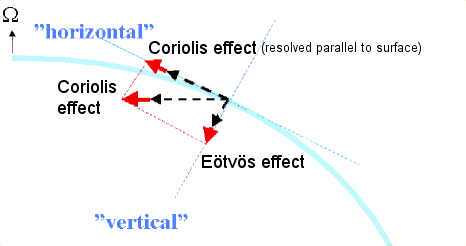
Os diagramas também mostram a componente na direção paralela à superfície local. Em meteorologia e oceanografia, é costume referir-se aos efeitos da componente paralela à superfície local como o força de Coriolis.

Ver também

• Física
• Força de Coriolis
• Geodesia
• Geofísica
• Meteorologia
• Oceanografia

Ligações externas

• O efeito de Coriolis