Quando duas ondas sonoras, com frequências diferentes, mas muito próximas, chegam aos nossos ouvidos simultaneamente, percebemos uma variação na intensidade do som resultante; ela aumenta e diminui alternadamente, produzindo um fenômeno chamado batimento. Esse batimento é resultante da interferência construtiva e destrutiva das duas ondas quando ficam em fase ou em oposição de fase. Se as duas frequências forem ficando próximas, o batimento ficará gradualmente mais lento e desaparecerá quando elas forem idênticas (uníssono).[1][2] Os batimentos entre dois tons podem ser percebidos pelo ouvido humano até uma frequência de 15Hz. Quando as frequências são superiores a 15Hz os batimentos individuais não podem ser distinguidos.[1][2]
Superposição de duas ondas de mesma direção
Os resultados da experimentação científica sugerem que o cérebro determina a altura de um som complexo procurando um padrão harmônico entre os seus componentes. O ouvido parece conseguir calcular as razões entre as frequências com grande precisão. Se a diferença entre as séries harmônicas de dois sons é demasiadamente grande, os vários componentes não se fundem e são ouvidos separadamente. Se a separação entre duas notas é reduzida a um tom (por exemplo, um Dó e um Ré), ouve-se uma dissonância - um som áspero. [3]
Equação do batimento
O número de batimentos por segundo é dado pela diferença entre as frequências das duas ondas componentes:[4]
Dedução da equação do batimento
A equação do batimento pode parecer trivial, porém sua dedução não é tão simples.[1] Suponhamos que as variações de pressão em certo local, produzidas por duas ondas sonoras de mesma amplitude sm, sejam
- e
Onde ω1 > ω2. De acordo com o princípio da superposição, a variação de pressão total é dada por
Usando a identidade trigonométrica
Podemos escrever a variação de pressão total na forma
Definindo
- e
Podemos reescrever a equação na forma
Vamos supor que as frequências angulares ω1 > ω2 das ondas que se combinam são quase iguais. Nesse caso podemos considerar a equação acima como uma função cosseno cuja frequência angular é ω e cuja amplitude é o valor absoluto do fator entre colchetes.
Um máximo de amplitude ocorre sempre que cos ω't é igual a 1 ou -1, o que acontece duas vezes em cada repetição da função cosseno. Como cos ω't tem frequência angular ω', a frequência angular ωbat com qual ocorre o batimento é ωbat = 2ω'. Assim podemos escrever
Como , esta equação também pode ser escrita na forma
Aplicação
Normalmente os músicos prestam atenção nos batimentos enquanto afinam seus instrumentos. Enquanto escutam algum batimento, é porque o instrumento está desafinado, logo alteram a afinação, até que a frequência de batimento diminua e o batimento desapareça, deixando assim o instrumento afinado.
Para afinar seu instrumento, um músico pode recorrer a um diapasão, um aparelho metálico, que emite uma frequência (normalmente Lá - 440Hz). Enquanto o diapasão emite a frequência, o músico toca a corda de seu instrumento simultaneamente, ajustando a tensão da corda ele tenta aproximar as duas frequências, fazendo com que o batimento seja imperceptível. [5][2]
Exemplos em reprodutores de áudio
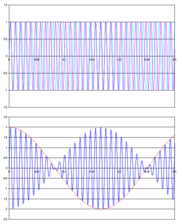
Referências
- ↑ 1,0 1,1 1,2 Halliday, David; Jearl Walker; Robert Resnick (2009). Fundamentos de Física 2 - Gravitação, Ondas, Termodinâmica. 2 8 ed. [S.l.]: LTC. ISBN 978-85-216-1606-1
- ↑ 2,0 2,1 2,2 Halliday, David; Jearl Walker; Robert Resnick (2007). Fundamentos de Física 2 - Gravitação, Ondas, Termodinâmica. 2 5 ed. [S.l.]: LTC. ISBN 978-85-216-1368-8
- ↑ «Interference beats and Tartini tones». School of Physics - UNSW
- ↑ Tipler, Paul A; Gene Mosca (2006). Física para cientistas e engenheiros 5 ed. [S.l.]: LTC. ISBN 85-216-1462-4
- ↑ «Batimentos e ressonância de diapasões analisados usando um osciloscópio» (PDF). Adenilson José Chiquito, Antonio Carlos Alonge Ramos - Departamento de Física, Universidade Federal de São Carlos










![{\displaystyle \cos a+\cos b=2\cos \left[{1 \over {2}}(a-b)\right]\cos \left[{1 \over {2}}(a+b)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8696060fff8ea921bf08485a751c8fdcfca9b042)
![{\displaystyle s=2s_{m}\cos \left[{1 \over {2}}(\omega _{1}-\omega _{2})t\right]\cos \left[{1 \over {2}}(\omega _{1}+\omega _{2})t\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aed765b271a0d1b84d15771cf8143beed0291ffb)


![{\displaystyle s(t)=[2s_{m}\cos \omega 't]\cos \omega t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf35abf5b2467040608c700e6c769d83d5121ae)



 " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="O que estudar para o enem 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Qual melhor curso para fazer em 2023"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Enem: Conteúdos E Aulas On-Line São Opção Para Os Estudantes"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Fazer Uma Carta De Apresentação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Como Escrever Uma Boa Redação"> " class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">
" class="attachment-atbs-s-4_3 size-atbs-s-4_3 wp-post-image" alt="Concurso INSS edital 2022 publicado">


